बहुपद शून्य

यह कैलकुलेटर आपको आपके द्वारा प्रदान किए गए किसी भी वैध बहुपद की बहुपद जड़ों की गणना करने की अनुमति देगा।यह बहुपद 1 या उच्चतर डिग्री 1 या उच्चतर का कोई बहुपद हो सकता है।

उदाहरण के लिए, आप एक क्यूबिक बहुपद प्रदान कर सकते हैं, जैसे कि p (x) = x^3 + 2x^2 - x + 1, या आप गैर -पूर्णांक गुणांक के साथ एक बहुपद प्रदान कर सकते हैं, जैसे कि P (x) = x^3 - 13/12 x^2 + 3/8 x - 1/24।

एक बार जब आप एक वैध बहुपद के साथ कैलकुलेटर प्रदान कर लेते हैं, जिसके लिए आप इसकी जड़ों की गणना करना चाहते हैं, तो आप "गणना" बटन पर क्लिक कर सकते हैं, और आपको प्रक्रिया का चरण-दर-चरण रन दिखाई देगा।

यह उल्लेख किया जाना चाहिए कि प्रक्रिया में केवल मूल विधियों को शामिल किया जाता है, जो जड़ों को खोजने के लिए उपयोग किए जाते हैं, जिसमें शामिल हैं सरायस और अँगुला , साथ ही उपयोग का उपयोग करना तमाम जब उपयुक्त हो।

सभी संभावित बहुपद के लिए सभी जड़ों को खोजने के लिए कोई सामान्य विधि नहीं है तमाम 5 से ऊपर, इसलिए यह कैलकुलेटर केवल उन जड़ें पाएगा जो इन उल्लिखित प्राथमिक तरीकों के साथ प्राप्त की जा सकती हैं।

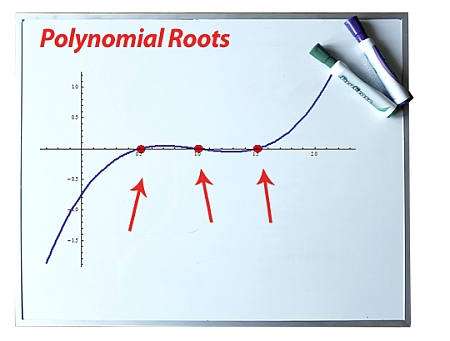
एक बहुपद की जड़ क्या है?

दिया गया बहुपदीय फलन \(p(x)\), हम कहते हैं कि \(x\) बहुपद की एक जड़ है यदि:

\[\displaystyle p(x) = 0 \]

एक बहुपद की जड़ें एक बहुपद की जड़ें हैं जो पॉलीनोमियल फ़ंक्शन हैं \(p(x)\) x- अक्ष को पार करती है।यह एक विचार प्राप्त करने के लिए एक अच्छा प्रतिनिधित्व है, लेकिन यह पूरी तरह से सटीक नहीं है क्योंकि कुछ जड़ें जटिल संख्या हो सकती हैं।तो, एक वास्तविक जड़ एक बिंदु होगा जहां \(p(x)\)।

निरीक्षण करें कि बहुपद की जड़ों को बहुपद शून्य भी कहा जाता है।

एक बहुपद के शून्य खोजने के लिए क्या कदम हैं?

• Letsunt 1: उन अभिव्यक्ति को पहचानें जिनके साथ आप काम करना चाहते हैं।सुनिश्चित करें कि यह एक बहुपद है और जितना संभव हो उतना सरल करें
• Therur the: हम उपयोग करेंगे फैक kburिंग इसकी जड़ खोजने के लिए दृष्टिकोण
• Theirण 3: के साथ प्राथमिक (तर्कसंगत) जड़ों को खोजने की कोशिश करना शुरू करें सरायस , और उपयोग करें अँगुला यदि संभव हो तो मूल बहुपद को कम करने के लिए
• Reyrur 4: यदि चरण 3 ने काम किया और आप मूल बहुपद को कम कर सकते हैं, तो पिछले चरणों को कम करने के लिए कम किए गए बहुपद को कारक करने का प्रयास करें

यह आमतौर पर आसान नहीं है, और यह कम्प्यूटेशनल रूप से गहन हो सकता है, और यह काम करने की गारंटी नहीं है, लेकिन यह सबसे अच्छा संभव दृष्टिकोण है यदि हम प्राथमिक विधियों का उपयोग करने के लिए प्रतिबंधित हैं।

जड़ों को खोजने का एकमात्र तरीका फैक्टरिंग है

Not really, but things go hand-to-hand. The तमाम बताता है कि \(x - a\) एक बहुपद \(p(x)\) का एक कारक है यदि और केवल अगर \(p(a) = 0\)।तो दूसरे शब्दों में, जड़ें और कारक अंतरंग रूप से जुड़े हुए हैं।

अब, डिग्री 2 के बहुपद के लिए (यह है, तमाम ) हम एक स्पष्ट सूत्र का उपयोग कर सकते हैं, जो कि अच्छी तरह से पता है तमाम ।

डिग्री 3 और 4 के लिए भी ऐसा ही होता है, हालांकि सूत्र प्राथमिक से दूर हैं।लेकिन डिग्री 5 और उच्चतर के लिए, ऐसा कोई फार्मूला नहीं है, जो गैलोइस और हाबिल द्वारा सिद्ध एक महत्वपूर्ण परिणाम है।इसलिए "सामान्य सूत्र" खोजने की कोई उम्मीद नहीं है, और यही वजह है कि अधिक लैक का उपयोग करें अँगुला पहुंचना।

बचने के लिए सामान्य गलतियाँ

अक्सर कई बार छात्र निराश हो जाते हैं कि वे किसी दिए गए की जड़ें नहीं पा सकते हैं बहुपदीय फलन , कहो \(p(x) = x^3+2 x^2-x+1 \), लेकिन उन्हें इस तथ्य का सामना करने की आवश्यकता है कि सभी बहुपदीय नहीं होंगे जो प्राथमिक उपकरणों का उपयोग करके हल किए जा सकेंगे।

दी, \(x^3+2 x^2-x+1 = 0 \) को हल करने के लिए एक सूत्र है, लेकिन यह प्राथमिक नहीं है, और यह उम्मीद नहीं है कि छात्र इसे जानते हैं।

सफलता के लिए युक्तियाँ

हमेशा एक मानसिक मानचित्र करने की कोशिश करें कि आपकी रणनीति क्या होगी: आपके पास मौजूद बहुपद, इसकी डिग्री, इसकी प्रमुख गुणांक और निरंतर गुणांक पर ध्यान दें।

अँगुला यदि आप कर सकते हैं, तो इसके व्यवहार का अंदाजा लगाने के लिए।क्या कोई स्पष्ट कारक है जिसका आप उपयोग कर सकते हैं?उनका उपयोग करें।हमेशा कारकों को याद रखें = जड़ें।

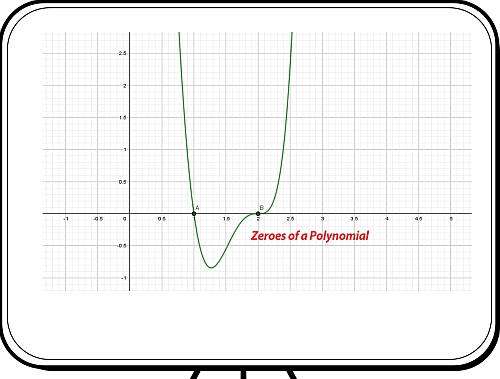
उदाहरण: एक बहुपद का शून्य

के शून्य क्या हैं: \(x^5 + x^4 - x^3 + x^2 - x + 1\)?

तमाम: इस उदाहरण के लिए हमें निम्नलिखित बहुपद के साथ प्रदान किया जाता है: \(\displaystyle p(x) = x^5+x^4-x^3+x^2-x+1\)।हम जड़ों को खोजने के लिए फैक्टरिंग दृष्टिकोण का उपयोग करेंगे।

Theirraur the therryrत नहीं प्रदान की गई बहुपद अभिव्यक्ति पहले से ही सरल है, इसलिए इसे और सरल बनाने के लिए कुछ भी नहीं है।

यह ध्यान दिया जा सकता है कि प्रदान किए गए बहुपद की डिग्री \(\displaystyle deg(p) = 5\) है।इसके अलावा, इसका प्रमुख गुणांक \(\displaystyle a_{5} = 1\) है और इसका निरंतर गुणांक \(\displaystyle a_0 = 1\) के बराबर है।

अब हम पूर्णांक संख्याओं की खोज करते हैं जो अग्रणी गुणांक \(a_{5}\) और निरंतर गुणांक \(a_0\) को विभाजित करते हैं, जिसका उपयोग तर्कसंगत उम्मीदवारों को खोजने के लिए किया जाता है।

▹ \(a_{5} = 1\) के डिवाइडर हैं: \(\pm 1\)।

▹ \(a_0 = 1\) के डिवाइडर हैं: \(\pm 1\)।

इसलिए, निरंतर शब्द के सभी कारकों को विभाजित करते हुए \(a_0 = 1\) \(a_{5} = 1\) के सभी विभाजकों द्वारा, हमें संभावित जड़ों की निम्नलिखित सूची मिलती है:

\[\pm \frac{ 1}{ 1}\]

अब, सभी संभावित समाधानों का मूल्यांकन किया जाना चाहिए।प्रत्येक उम्मीदवार के परीक्षण से प्राप्त परिणाम इस प्रकार हैं:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle \left(-1\right)^5+\left(-1\right)^4-\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+1 & = & \displaystyle 4 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^5+1^4-1^3+1^2-1+1 & = & \displaystyle 2 \ne 0 \\\\ \end{array}\]

चूंकि मैनुअल निरीक्षण के माध्यम से कोई तर्कसंगत जड़ों की पहचान नहीं की गई थी, इसलिए बुनियादी तकनीकों का उपयोग करके आगे सरलीकरण संभव नहीं है और प्रक्रिया इस कदम के साथ समाप्त होती है।

तिहाई : नतीजतन, कोई सरलीकरण प्राप्त नहीं किया गया था और मूल तकनीकों के माध्यम से बहुपद की कोई जड़ों की पहचान नहीं की गई थी

उदाहरण: जड़ों की गणना एक द्विघात कार्य

के समाधान की गणना करें: \(3x^2 - 2x - 4 = 0\)।

तमाम: हमें दिए गए द्विघात समीकरण को हल करने की आवश्यकता है \(\displaystyle 3x^2-2x-4=0\)।

फॉर्म के द्विघात समीकरण के लिए जड़ें \(a x^2 + bx + c = 0\) निम्नलिखित समीकरण का उपयोग करके गणना की जाती है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस संदर्भ में, समीकरण को हल करने की आवश्यकता है \(\displaystyle 3x^2-2x-4 = 0\), यह दर्शाता है कि संबंधित गुणांक हैं:

\[a = 3\] \[b = -2\] \[c = -4\]

सबसे पहले, हम भेदभावपूर्ण की गणना करके जड़ों की प्रकृति का निर्धारण करेंगे।विभेदक की गणना निम्नानुसार की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(3\right)\cdot \left(-4\right) = 52\]

चूंकि इस मामले में हमें भेदभावपूर्ण लगता है \(\Delta = \displaystyle 52 > 0\), जो सकारात्मक है, इसलिए, समीकरण में दो अलग -अलग वास्तविक जड़ें हैं।

इससे हमें मिलता है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(3\right)\left(-4\right)}}{2\cdot 3} = \displaystyle \frac{2 \pm \sqrt{52}}{6}\]

तो फिर, हम पाते हैं कि:

\[ x_1 = \frac{2}{6}-\frac{1}{6}\sqrt{52}=\frac{2}{6}-\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}-\frac{1}{3}\sqrt{13}=\frac{1}{3}-\frac{1}{3}\sqrt{13} \] \[x_2 = \frac{2}{6}+\frac{1}{6}\sqrt{52}=\frac{2}{6}+\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}+\frac{1}{3}\sqrt{13}=\frac{1}{3}+\frac{1}{3}\sqrt{13}\]

हम पाते हैं कि समीकरण \( \displaystyle 3x^2-2x-4 = 0 \), दो वास्तविक जड़ें हैं, इसलिए फिर:

\[\displaystyle 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

तो फिर मूल बहुपद को \(\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right) \) के रूप में फैक्टर किया जाता है, जो कारक को पूरा करता है।

तिहाई : इसलिए, हमें जिस कारक की तलाश है, वह द्वारा दिया गया है:

\[\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

पाए गए जड़ों \(-\frac{1}{3}\sqrt{13}+\frac{1}{3}\) और \(\frac{1}{3}\sqrt{13}+\frac{1}{3}\) हैं।

उदाहरण: बहुपद शून्य

निम्नलिखित बहुपद के शून्य की गणना करें: \(p(x)= x^3 - \frac{13}{12} x^2 + \frac{3}{8} x - \frac{1}{24} \)।

तमाम: अंत में, इस उदाहरण में हमारे पास: \(\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24}\)।

सना हुआ: प्रदान की गई बहुपद अभिव्यक्ति अप्रासंगिक है, इसलिए सरल बनाने के लिए कुछ भी नहीं है।हम इसे कारक करने के लिए आगे बढ़ सकते हैं।

देखें कि दिए गए बहुपद की डिग्री \(\displaystyle deg(p) = 3\) है, इसका प्रमुख गुणांक \(\displaystyle a_{3} = 1\) है और इसका निरंतर गुणांक \(\displaystyle a_0 = -\frac{1}{24}\) है।

सराय : हम तर्कसंगत शून्य प्रमेय के साथ पहले सरल तर्कसंगत जड़ों को खोजने की कोशिश करेंगे।

अगला कार्य पूर्णांक संख्याओं को खोजने के लिए है जो अग्रणी गुणांक \(a_{3}\) और निरंतर गुणांक \(a_0\) को विभाजित करते हैं, इसका उपयोग हमारे उम्मीदवारों को बहुपद समीकरण के शून्य होने के लिए बनाने के लिए किया जाएगा।

S टिपtun: इस मामले में, हम मानते हैं कि निरंतर और अग्रणी गुणांक दोनों के लिए हमें समीकरण के दोनों किनारों को \(24\) द्वारा बढ़ाने की आवश्यकता है।समकक्ष समीकरण है:

\[24x^3-26x^2+9x-1 = 0\]

▹ \(a_{3} = 24\) के डिवाइडर हैं: \(\pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 8,\pm 12,\pm 24\)।

▹ \(a_0 = -1\) के डिवाइडर हैं: \(\pm 1\)।

इसलिए, निरंतर गुणांक के प्रत्येक विभक्त को विभाजित करना \(a_0 = -1\) प्रमुख गुणांक के प्रत्येक विभक्त द्वारा \(a_{3} = 24\), हम उम्मीदवारों की निम्नलिखित सूची को जड़ें पाते हैं:

\[\pm \frac{ 1}{ 1},\pm \frac{ 1}{ 2},\pm \frac{ 1}{ 3},\pm \frac{ 1}{ 4},\pm \frac{ 1}{ 6},\pm \frac{ 1}{ 8},\pm \frac{ 1}{ 12},\pm \frac{ 1}{ 24}\]

अब, सभी उम्मीदवारों को यह देखने के लिए परीक्षण करने की आवश्यकता है कि क्या वे एक समाधान हैं।प्रत्येक उम्मीदवार के परीक्षण से निम्नलिखित प्राप्त किया जाता है:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle 24\cdot \left(-1\right)^3-26\cdot \left(-1\right)^2+9\cdot \left(-1\right)-1 & = & \displaystyle -60 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 24\cdot 1^3-26\cdot 1^2+9\cdot 1-1 & = & \displaystyle 6 \ne 0 \\\\ x & = & \displaystyle -\frac{1}{2} &:&    & \displaystyle 24\left(\frac{-1}{2}\right)^3-26\left(\frac{-1}{2}\right)^2+9\left(-\frac{ 1}{ 2}\right)-1 & = & \displaystyle -15 \ne 0 \\\\ x & = & \displaystyle \frac{1}{2} &:&    & \displaystyle 24\left(\frac{1}{2}\right)^3-26\left(\frac{1}{2}\right)^2+9\cdot \frac{1}{2}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{3} &:&    & \displaystyle 24\left(\frac{-1}{3}\right)^3-26\left(\frac{-1}{3}\right)^2+9\left(-\frac{ 1}{ 3}\right)-1 & = & \displaystyle -\frac{70}{9} \ne 0 \\\\ x & = & \displaystyle \frac{1}{3} &:&    & \displaystyle 24\left(\frac{1}{3}\right)^3-26\left(\frac{1}{3}\right)^2+9\cdot \frac{1}{3}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{4} &:&    & \displaystyle 24\left(\frac{-1}{4}\right)^3-26\left(\frac{-1}{4}\right)^2+9\left(-\frac{ 1}{ 4}\right)-1 & = & \displaystyle -\frac{21}{4} \ne 0 \\\\ x & = & \displaystyle \frac{1}{4} &:&    & \displaystyle 24\left(\frac{1}{4}\right)^3-26\left(\frac{1}{4}\right)^2+9\cdot \frac{1}{4}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{6} &:&    & \displaystyle 24\left(\frac{-1}{6}\right)^3-26\left(\frac{-1}{6}\right)^2+9\left(-\frac{ 1}{ 6}\right)-1 & = & \displaystyle -\frac{10}{3} \ne 0 \\\\ x & = & \displaystyle \frac{1}{6} &:&    & \displaystyle 24\left(\frac{1}{6}\right)^3-26\left(\frac{1}{6}\right)^2+9\cdot \frac{1}{6}-1 & = & \displaystyle -\frac{1}{9} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{8} &:&    & \displaystyle 24\left(\frac{-1}{8}\right)^3-26\left(\frac{-1}{8}\right)^2+9\left(-\frac{ 1}{ 8}\right)-1 & = & \displaystyle -\frac{165}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{8} &:&    & \displaystyle 24\left(\frac{1}{8}\right)^3-26\left(\frac{1}{8}\right)^2+9\cdot \frac{1}{8}-1 & = & \displaystyle -\frac{15}{64} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{12} &:&    & \displaystyle 24\left(\frac{-1}{12}\right)^3-26\left(\frac{-1}{12}\right)^2+9\left(-\frac{ 1}{ 12}\right)-1 & = & \displaystyle -\frac{35}{18} \ne 0 \\\\ x & = & \displaystyle \frac{1}{12} &:&    & \displaystyle 24\left(\frac{1}{12}\right)^3-26\left(\frac{1}{12}\right)^2+9\cdot \frac{1}{12}-1 & = & \displaystyle -\frac{5}{12} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{24} &:&    & \displaystyle 24\left(\frac{-1}{24}\right)^3-26\left(\frac{-1}{24}\right)^2+9\left(-\frac{ 1}{ 24}\right)-1 & = & \displaystyle -\frac{91}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{24} &:&    & \displaystyle 24\left(\frac{1}{24}\right)^3-26\left(\frac{1}{24}\right)^2+9\cdot \frac{1}{24}-1 & = & \displaystyle -\frac{385}{576} \ne 0 \\\\ \end{array}\]

लेकिन चूंकि हमने तर्कसंगत उम्मीदवारों के बीच सभी आवश्यक जड़ें पाई हैं, इसलिए हम पाते हैं कि \(\displaystyle x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \), तो: तो:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \]

जो कारक प्रक्रिया को पूरा करता है।

शराबी : इसलिए, अंतिम कारक है:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right)\]

इसलिए, पाए गए जड़ें \(\frac{1}{2}\), \(\frac{1}{3}\) और \(\frac{1}{4}\) हैं।

अन्य उपयोगी बहुपद कैलकुलेटर

एक बहुपद के शून शून शून शून बीजगणित के एक शिखर है, इस हद तक कि बीजगणित का मौलिक प्रमेय डिग्री एन के बहुपद के लिए एन जड़ों के अस्तित्व के बारे में है।वे जड़ें सभी वास्तविक नहीं होंगी, और उनमें से कुछ (या उन सभी) को कम्पेक्स नंबर हो सकते हैं।

अंततः, बीजगणित और कैलकुलस में लगभग हर एक समस्या को एक बहुपद की जड़ों को खोजने के लिए कम किया जा सकता है, जिसमें हल करना शामिल है बहुपद rayrण जैसे कि आप उदाहरण के लिए मिलेंगे, जब देख रहे हैं राग \(y = x^2\) और \(y = x^3\)।