सामान्य संभाव्यता प्लॉट के बारे में अधिक जानकारी

सामान्य संभाव्यता प्लॉट एक प्लॉट है जिसका उपयोग आम तौर पर उस वितरण की सामान्यता का आकलन करने के लिए किया जाता है जिससे पारित नमूना डेटा संबंधित होता है।

नॉर्मलिटी प्लॉट के विभिन्न प्रकार हैं (पीपी, क्यूक्यू और अन्य किस्में), लेकिन वे सभी एक ही विचार के आधार पर काम करते हैं। मानक नॉर्मल डिस्ट्रीब्यूशन के सैद्धांतिक क्वांटाइल को प्रेक्षित क्वांटाइल के विरुद्ध ग्राफ़ किया जाता है।

इसलिए, यदि नमूना डेटा किसी सामान्य वितरित जनसंख्या , तो सामान्य संभावना प्लॉट 45 जैसा दिखना चाहिए ^हे रेखा, इसके बारे में यादृच्छिक भिन्नताओं के साथ। यदि ऐसा नहीं है, और सामान्य संभाव्यता प्लॉट का पैटर्न सामान्य संभाव्यता प्लॉट से महत्वपूर्ण रूप से/व्यवस्थित रूप से अलग हो जाता है, तो किसी को संदेह होना चाहिए कि वितरण सामान्य नहीं है।

आप सामान्य संभाव्यता प्लॉट की गणना कैसे करते हैं?

एक सामान्य संभाव्यता प्लॉट बनाने के लिए आपको एक विशिष्ट क्रम में कई ठोस कदम उठाने की आवश्यकता होती है

1. इस ठोस मामले में, डेटा को आरोही क्रम में व्यवस्थित किया जाता है, और हम ऐसे डेटा को \(X_1, X_2, ...., X_i , ...., X_n\) कहते हैं।
2. क्रमबद्ध आंकड़ों के इस अनुक्रम में प्रत्येक \(X_i\) के लिए, हम सैद्धांतिक आवृत्तियों \(f_i\) की गणना करते हैं, जिन्हें निम्नलिखित सूत्र का उपयोग करके अनुमानित किया जाता है:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. फिर हम \(z_i\) की भी गणना करते हैं, जो संबंधित z-स्कोर है
\[ z_i = \Phi^{-1}(f_i)\]
4. फिर, क्षैतिज अक्ष पर क्रमित X-मान (आपका नमूना डेटा) और आपके ऊर्ध्वाधर अक्ष पर संगत \(z_i\) मान प्लॉट करके सामान्य संभाव्यता प्लॉट प्राप्त किया जाता है।

सामान्य संभाव्यता प्लॉट एक्सेल

आप एक्सेल में एक सामान्य संभाव्यता ग्राफ बना सकते हैं, लेकिन इसमें कुछ समय लगता है।

सामान्य वितरण और अन्य के लिए कैलकुलेटर

अन्य चार्ट निर्माता जिनका आप उपयोग कर सकते हैं वे हैं हमारे सामान्य वितरण ग्राफर , बिखरने की साजिश निर्माता या हमारे पारेतो चार्ट निर्माता .

उदाहरण: सामान्य संभाव्यता प्लॉट की गणना

प्रश्न आपको निम्नलिखित नमूना डेटा प्रदान किया गया है: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 और 23. एक सामान्य प्रायिकता प्लॉट का निर्माण करें।

समाधान:

हमें एक सामान्य संभाव्यता प्लॉट बनाने की आवश्यकता है। ये नमूना डेटा प्रदान किए गए हैं:

अवलोकन:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

सैद्धांतिक आवृत्तियों \(f_i\) के साथ-साथ \(i = 1, 2, ..., 33\) के लिए संबद्ध z-स्कोर \(z_i\) की गणना करने की आवश्यकता है:

ध्यान दें कि सैद्धांतिक आवृत्तियों \(f_i\) को निम्नलिखित सूत्र का उपयोग करके अनुमानित किया गया है:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

जहाँ \(i\) क्रमबद्ध डेटासेट में स्थिति से मेल खाता है, और \(z_i\) संबंधित संबद्ध z-स्कोर है। इसकी गणना इस प्रकार की जाती है

\[ z_i = \Phi^{-1}(f_i)\]

निम्नलिखित तालिका प्राप्त होती है

स्थिति (i)	एक्स (आरोही क्रम)	एफ मैं	जेड मैं
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

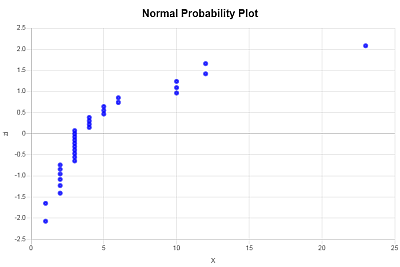
सामान्य संभाव्यता प्लॉट क्षैतिज अक्ष पर X-मान (आपका नमूना डेटा) और आपके ऊर्ध्वाधर अक्ष पर संगत \(z_i\) मान प्लॉट करके प्राप्त किया जाता है। निम्नलिखित सामान्यता प्लॉट प्राप्त किया जाता है: