फ़ंक्शन की अवधारणा अत्यंत महत्वपूर्ण है और यह गणित में बिल्कुल सर्वव्यापी है। यही कारण है कि कुछ अच्छाइयों को समझने का प्रयास करने से पहले हमें इसे एक अच्छा ब्रश अप देने की आवश्यकता है, जो बाद में कैलकुलस विषयों, जैसे कि भेदभाव और एकीकरण में गहराई से आने पर आएगा।

एक सेट क्या है?

पहला तत्व जिसे हमें समझने की जरूरत है वह है a . की अवधारणा सेट . एक सेट बस तत्वों का एक संग्रह है। तो फिर, एक समुच्चय को यह जानने के तरीके से काफी सरलता से परिभाषित किया जाता है कि कौन से तत्व समुच्चय से संबंधित हैं और कौन से तत्व नहीं हैं। यह एक बहुत ही सरल कार्य प्रतीत होता है और सेट के सिद्धांत को केवल यह निर्धारित करने के लिए कि कौन से तत्व एक सेट से संबंधित हैं, स्पष्ट नियम होने चाहिए।

उदाहरण के लिए, आइए हम सम संख्या के समुच्चय को परिभाषित करें, और हम इसे \(E\) कहते हैं। यह एक सेट भी क्यों है? क्योंकि यह निर्धारित करने के लिए एक स्पष्ट नियम है कि कौन से तत्व \(E\) से संबंधित हैं: एक वास्तविक संख्या \(x\) \(E\) से संबंधित है यदि यह 2 से विभाज्य है। नियम प्रत्येक वास्तविक संख्या के लिए स्पष्ट रूप से काम करता है यह निर्धारित करता है कि यह \(E\) से संबंधित है या नहीं। मैं "स्पष्ट रूप से" क्यों कहता हूं और दोहराता रहता हूं। क्योंकि यह महत्वपूर्ण है। स्पष्ट रूप से इसका मतलब है कि यह निष्कर्ष निकालने का कोई तरीका नहीं है कि दिए गए \(x\) दोनों \(E\) से संबंधित हैं और नहीं हैं। दुर्भाग्य से कभी-कभी चीजें हमारी कल्पना से परे हो जाती हैं। हमारे अंतर्ज्ञान के विपरीत, संबंधित के एक सरल नियम के साथ परिभाषित एक सेट एक अस्पष्ट (विरोधाभासी) संबंधित वर्गीकरण को जन्म दे सकता है, जैसा कि बर्ट्रेंड रसेल ने अपने प्रसिद्ध विरोधाभास में दिखाया है। रसेल ने दिखाया कि एक सेट क्या है की अधिक सावधानीपूर्वक परिभाषा का उपयोग किया जाना चाहिए।

सभी व्यावहारिक उद्देश्यों के लिए, हम तत्वों के संग्रह के रूप में एक सेट के बारे में सोचेंगे, जो संबंधित के नियम द्वारा परिभाषित किया जा सकता है .

दो सेट का उत्पाद क्या है?

ऊपर दी गई परिभाषा के संदर्भ में \(A\) और \(B\) सेट होने दें। दो सेटों का उत्पाद \(A\times B\) एक और सेट है, जिसे \(\left( a, b \right)\) फॉर्म के सभी संभावित ऑर्डर किए गए जोड़े के सेट के रूप में परिभाषित किया गया है, जहां \(a\) \(A\) से संबंधित है और \(b\) \(B\) से संबंधित है। तो फिर, \(A\times B\) एक समुच्चय है, और इसके तत्वों को \(\left( a ,b \right)\) के रूप में क्रमित युग्म हैं। उस अंकन को आपको प्रभावित न करने दें। जब मैं कहता हूं "फॉर्म \(\left( a, b \right)\) के ऑर्डर किए गए जोड़े", प्रतीक \(\left( a, b \right)\) एक बना हुआ प्रतीक है, एक तत्व को इंगित करने के लिए जो दो संस्थाओं \(a\) और \(b\) से बना है, और पहले तत्व को \(a\) के रूप में और दूसरे तत्व को \(b\) के रूप में पहचानें। . बस, इतना ही। \(\left( a,b \right)\) के बजाय, हम प्रतीक \(a\_b\) को चुन सकते थे, और यह ठीक काम करता।

आपको मुझे माफ़ करना होगा, लेकिन मुझे दो समुच्चयों के गुणनफल की गणितीय परिभाषा लिखनी है (हम समुच्चयों को भी गुणा कर सकते हैं….आपने क्या सोचा, हम केवल संख्याओं के साथ रुकेंगे, उह?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

परिभाषा लिखने का कारण यह है कि आप इसे देखें और पहचानें कि कैसे एक बहुत ही कॉम्पैक्ट नोटेशन का उपयोग करके हम ठीक उसी तरह कह रहे हैं जिस तरह से मैंने इसे उपरोक्त पैराग्राफ में शब्दों के साथ परिभाषित किया है। मुझे आशा है कि आप गणित के कथनों को पढ़ने के लिए कुछ डर कम कर देंगे। गणितज्ञ कभी-कभी फंकी लोग हो सकते हैं, लेकिन वे अच्छे, स्पष्ट और कॉम्पैक्ट नोटेशन ढूंढते हैं। और फलस्वरूप, गणित की भाषा पढ़ने में बहुत आसान है। सही? सही? कृपया मुझे बताओ मैं सही हूँ ...

एक साइड नोट, ऐतिहासिक कारणों से, दो सेट \(A\times B\) के गुणनफल को सामान्यतः a . के रूप में संदर्भित किया जाता है कार्तीय गुणन .

अब, एक समारोह की परिभाषा (अंत में)

ठीक है, मैंने झूठ बोला, फ़ंक्शन क्या है, इसे परिभाषित करने से पहले एक और कदम है। हमें की अवधारणा को परिभाषित करने की आवश्यकता है संबंध . एक रिश्ता क्या है? एक अंग्रेजी शब्द के रूप में इसके सामान्य उपयोग से परे, एक संबंध कार्टेशियन उत्पाद का एक सबसेट है। कार्टेशियन उत्पाद का कोई भी सबसेट एक संबंध है। तो फिर अगर \(A\) और \(B\) सेट हैं, तो एक सेट \(R\) एक संबंध है यदि \(R\subseteq A\times B\)। चूँकि किसी भी समुच्चय को स्वयं का उपसमुच्चय माना जा सकता है, तो सभी कार्तीय गुणनफल स्वयं संबंध होते हैं।

इसे एक फ्रेम पर रखें:

एक संबंध एक सेट है जो एक कार्टेशियन उत्पाद का सबसेट है

आइए हम और अधिक ग्राफिकल हो जाएं। समुच्चय \(A=\left[ 0,1 \right]\) पर विचार करें (जो सभी वास्तविक संख्याएँ हैं जो 0 से अधिक या उसके बराबर हैं, और वे 1 से भी कम या बराबर हैं)। कार्टेशियन उत्पाद \(A\times A\) क्या है? आइए तोते जो हमने अभी सीखा है। कार्टेशियन उत्पाद \(A\times A\) \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) है, इस मामले में सभी जोड़े\(\left( x, y \right)\) का सेट है, जहां \(x\) और \(y\) दोनों \(\left[ 0,1 \right]\) से संबंधित हैं। कार्टेशियन उत्पाद आमतौर पर ग्राफ के लिए आसान होते हैं। नीचे छायांकित क्षेत्र को देखें:

अब क्या संबंध बनाएंगे? हम उपरोक्त सभी छायांकित क्षेत्र को "नक्काशी" कर सकते हैं, और जो बचा है वह \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) में एक संबंध है। उदाहरण के लिए, हम निम्नलिखित उप-क्षेत्र प्राप्त करने के लिए "कोनों" को काट सकते हैं:

उपरोक्त क्षेत्र (सेट) एक संबंध है। क्यों? क्योंकि यह कार्तीय गुणन \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) का उपसमुच्चय है। लेकिन हम और भी अधिक तराश सकते हैं। एक चौथाई सर्कल बनाने के बारे में कैसे? नीचे क्षेत्र देखें।

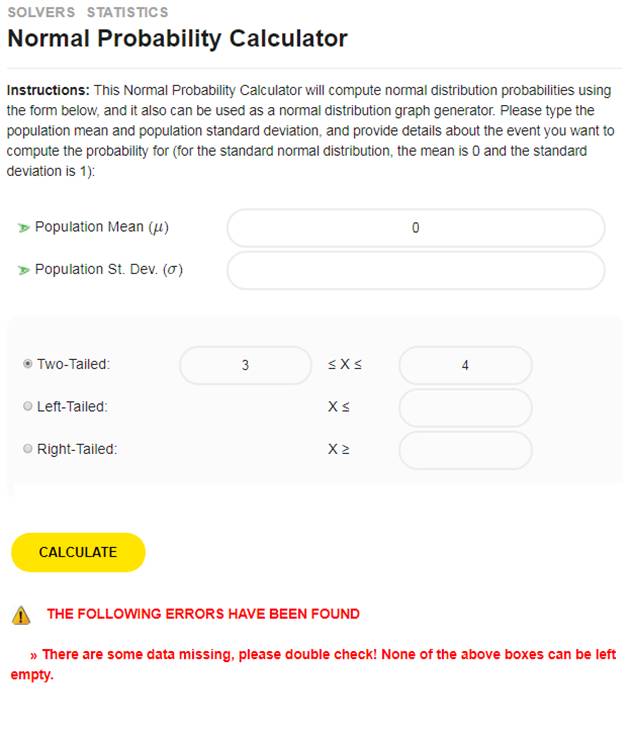
उपरोक्त क्षेत्र (सेट) एक संबंध है। क्यों? दोबारा, क्योंकि यह कार्टेशियन उत्पाद \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) का सबसेट है।

अब, मैं आपको \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) में दो संबंधों का एक उदाहरण देता हूं। नीचे दिए गए ग्राफ़ को देखें:

संबंध 1

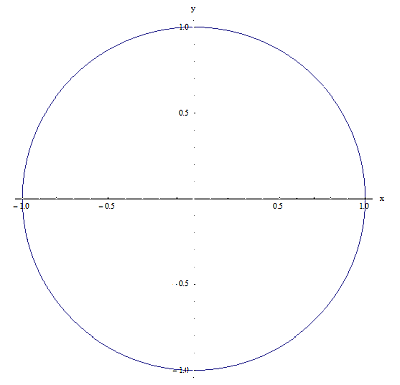
संबंध 2

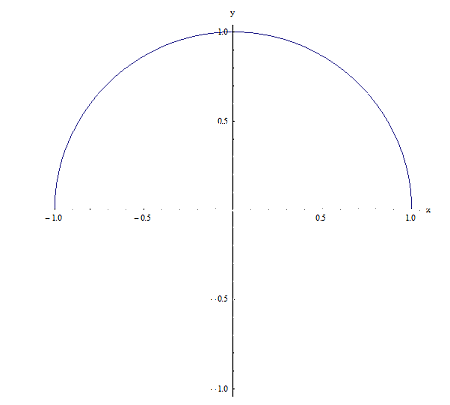
वे दोनों स्पष्ट रूप से संबंध हैं (क्योंकि वे दोनों कार्टेशियन उत्पाद \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) में निहित हैं, लेकिन उनके पास एक महत्वपूर्ण अंतर है: संबंध 1 के लिए, \(\left[ -1,1 \right]\) पर दिए गए बिंदु x के लिए, दो बिंदु \({{y}_{1}}\)और \({{y}_{2}}\) जिनके पास \(\left( x,{{y}_{1}} \right)\) और \(\left( x,{{y}_{2}} \right)\) संपत्ति है संबंध 1 के लिए। उदाहरण के लिए x = 0 के लिए, दो बिंदु हैं \({{y}_{1}}=1\) और \({{y}_{2}}=-1\) जैसे कि \(\left( 0,1 \right)\)और\(\left( 0,-1 \right)\) संबंध 1 से संबंधित हैं। अब, संबंध 2 के लिए ऐसा नहीं है क्योंकि, उदाहरण के लिए, x = 0 के लिए यह केवल \(y=1\) है। बिंदु \(\left( 0,1 \right)\) संबंध 1 से संबंधित है।

अंत में हम एक फ़ंक्शन को परिभाषित कर सकते हैं: एक फ़ंक्शन \(R\) एक सेट है जो एक संबंध है और इसमें यह गुण भी है कि यदि बिंदु \(\left( x,y \right)\) \(R\) से संबंधित है, तो कोई अन्य बिंदु \(\bar{y}\) \(y\) से भिन्न नहीं है जिसमें संपत्ति है \(\left( x,\bar{y} \right)\) \(R\) से संबंधित है। भी। दूसरे शब्दों में, एक फ़ंक्शन अतिरिक्त आवश्यकता के साथ एक संबंध है कि प्रत्येक \(x\) अपने डोमेन में केवल एक \(y\) के साथ जुड़ा हुआ है।

फ़ंक्शन और संबंध के बीच अंतर करना कैसे जानते हैं ??

गैजेट्स! हम "वर्टिकल लाइन टेस्ट" नामक एक छोटी सी चाल का उपयोग करते हैं: हम एक काल्पनिक लंबवत रेखा खींचते हैं, और हम इसे बाएं से दाएं घुमाते हुए घूमते हैं, और जहां लंबवत रेखा संबंध को छेड़छाड़ करती है उसका मानसिक नक्शा बनाते हैं।

• यदि किसी बिंदु पर, ऊर्ध्वाधर रेखा संबंध को एक से अधिक बिंदुओं पर काटती है, तो संबंध लंबवत रेखा परीक्षण में विफल हो जाता है, और तब संबंध एक फ़ंक्शन नहीं होता है

• यदि किसी भी बिंदु पर, ऊर्ध्वाधर रेखा एक से अधिक बिंदु पर कहीं भी संबंध को नहीं काटती है, तो संबंध लंबवत रेखा परीक्षण पास करता है, और फिर संबंध एक कार्य है

नीचे दो उदाहरण देखें:

उदाहरण 1: यह लंबवत रेखा परीक्षण में विफल रहता है क्योंकि चित्र में दिखाई गई लंबवत रेखा संबंध को एक से अधिक बिंदुओं पर काटती है: एक समारोह नहीं

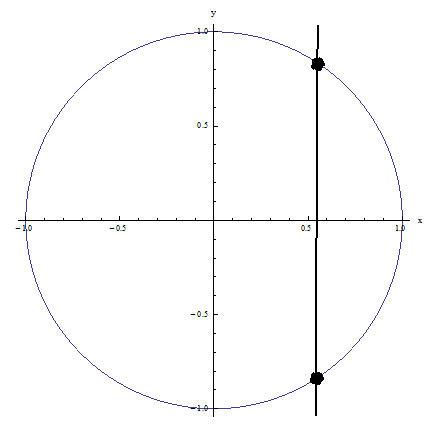
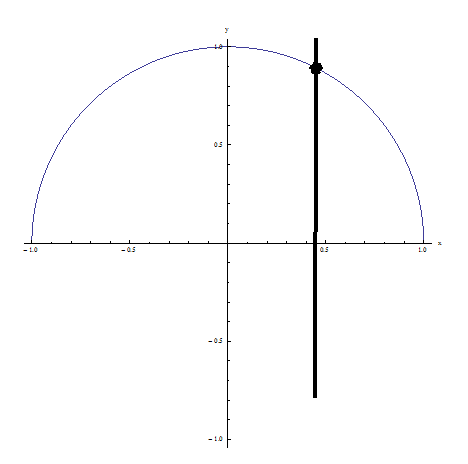
उदाहरण 2: यह ऊर्ध्वाधर रेखा परीक्षण पास करता है क्योंकि कोई भी ऊर्ध्वाधर रेखा संबंध को एक से अधिक बिंदुओं पर नहीं काटती है: यह एक कार्य है!

कई ग्राफिकल एप्लिकेशन हैं जिन्हें की गणना सहित कार्यों के साथ संचालित किया जा सकता है क्षैतिज अनंतस्पर्शी , लंबवत स्पर्शोन्मुख, और तिरछी स्पर्शोन्मुख यदि लागू हो।