त्रिकोणमितीय कार्य ग्राफर

त्रिकोणमितीय कार्यों में संपत्ति होती है कि वे अपने व्यवहार को दोहराते हैं।यह है, वे आवधिक हैं।गणितीय रूप से, इसका मतलब है कि संपत्ति के साथ एक संख्या \(P\) है

\[f(x+P) = f(x)\]

\(x\) के सभी मूल्यों के लिए।वह संख्या \(P\) कहा जाता है अवधि ।यह सब कह रहा है कि फ़ंक्शन का व्यवहार खुद को rabanata है ट्रिग ग्राफ में हर \(P\) x- अक्ष में इकाइयाँ।

निरीक्षण करें कि इस कैलकुलेटर के लिए आपके द्वारा प्रदान किए जाने वाले सभी त्रिकोणमितीय कार्य, तर्क \(x\) माना जाता है Rup ya rabanata taana ।

आवधिक कार्यों का उदाहरण

उदाहरण के लिए, साइन फ़ंक्शन के मामले के लिए, \(f(x) = \sin x\), ग्राफ नीचे दिखाया गया है:

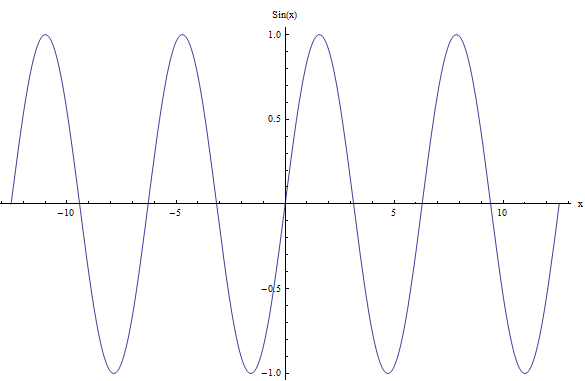
आप देख सकते हैं कि फ़ंक्शन का व्यवहार खुद को दोहराता है।वास्तव में, आप लंबाई का कोई भी अंतराल ले सकते हैं \(2\pi\) और लंबाई का अगला अंतराल \(2\pi\) फ़ंक्शन के आकार के संदर्भ में पिछले एक के समान होगा।

ऐसा क्यों होता है?क्योंकि \(\sin(x + 2\pi) = \sin(x)\), सभी के लिए \(x\), और फिर फ़ंक्शन आवधिक है।

मैं इस त्रिकोणमितीय फ़ंक्शन प्लॉटर के साथ क्या ग्राफ़ कर सकता हूं?

आप किसी भी त्रिकोणमितीय फ़ंक्शन की साजिश कर सकते हैं।सबसे आम उपयोग साइन और कोसाइन को रेखांकन के लिए है, लेकिन आप इसे किसी भी ट्रिग फ़ंक्शन के लिए उपयोग कर सकते हैं।

आप देखेंगे कि आवधिक कार्यों को अन्य बीजगणितीय अभिव्यक्तियों के साथ यौगिक करके अधिक जटिल होने के लिए बनाया जा सकता है।

उदाहरण के लिए, फ़ंक्शन का व्यवहार क्या है \(f(x) = 3\sin(2x+1)-4\) ठीक है, यह आवधिक भी है?हाँ, आप शर्त लगाते हैं।फ़ंक्शन का व्यवहार \(f(x) = 3\sin(2x+1)-4\) फ़ंक्शन के समान सभी तरीकों से है \(f(x) = \sin x\)।

यह त्रिकोणमितीय फ़ंक्शन ग्राफर आपको ग्राफ और विशिष्ट विशेषताओं (अवधि, आवृत्ति, आयाम, चरण शिफ्ट और ऊर्ध्वाधर पारी) को अधिक जटिल त्रिकोणमितीय कार्यों के रूप में खोजने में मदद करेगा, जैसे कि \(f(x) = 3\cos(\pi(x-2)+3)-\frac{\pi}{4}\)

क्या कोष्ठक मायने रखते हैं?

संक्षिप्त उत्तर है: यह निर्भर करता है।कभी -कभी आपके पास एक सरल अभिव्यक्ति होगी जहां केवल योग, या केवल गुणन मौजूद हैं, जिस स्थिति में संबंधी संपत इस्तेमाल किया जा सकता है।लेकिन जब मिश्रित संचालन बहुत बार होते हैं तो आप फ़ंक्शन को तोड़े या इसे बदलने के बिना कोष्ठक को छोड़ या बदल नहीं सकते।

ग्राफ़ कैलकुलेटर

यह ग्राफर केवल त्रिकोणमितीय कार्यों से संबंधित है।के लिए तमाम , आप हमारा उपयोग कर सकते हैं तमाम , जो किसी भी कार्य को लेगा, न केवल त्रिकोणमितीय वाले।

ट्रिग ग्राफ का उदाहरण

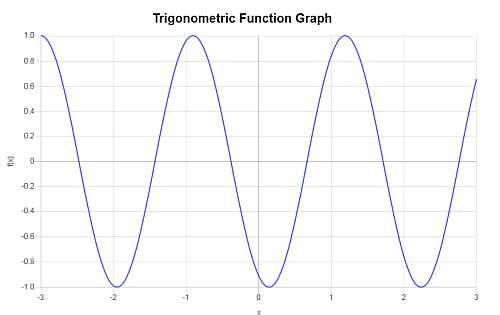
प्रश्न : फ़ंक्शन पर विचार करें \(f(x) = \sin(3x-2)\)।अवधि, आवृत्ति, आयाम और चरण बदलाव का पता लगाएं।इसके अलावा, फ़ंक्शन का एक ग्राफ प्रदान करें।

समाधान:

निम्नलिखित फ़ंक्शन प्रदान किया गया है:

\[f(x) = \sin\left(3x-2\right)\]

त्रिकोणमितीय फ़ंक्शन के तर्क के आधार पर जो पारित किया गया था, आवृत्ति और अवधि की गणना निम्नानुसार की जाती है:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

और भी

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

प्रदान किए गए त्रिकोणमितीय फ़ंक्शन के आधार पर, \(f(x) = \sin\left(3x-2\right)\), हम इसे प्राप्त करते हैं:

• इस मामले में आयाम \(A = 1\) है।

• चरण शिफ्ट \(\displaystyle\frac{2}{3} = 0.6667\) के बराबर है।

• ऊर्ध्वाधर पारी \( 0\) के बराबर है।

उपरोक्त जानकारी के आधार पर, निम्नलिखित ग्राफ प्राप्त किया जाता है: