बहुपद कार्य

इस तंग आपके द्वारा प्रदान की गई किसी भी बहुपद अभिव्यक्ति की गणना और सरल करके, बहुपद कार्यों की गणना करने में आपकी सहायता करेगा।

आप किसी भी प्रकार की अभिव्यक्ति प्रदान कर सकते हैं जिसमें बहुपद शामिल हैं, और गणना आयोजित की जाएगी और आवश्यक सरलीकरण कदम उठाए जाएंगे, इसलिए एक बहुपद कार्य को अपने सबसे कॉम्पैक्ट रूप में छोड़ने के लिए।फिर, एक बहुपद ग्राफ प्रदान किया जाएगा

फिर, एक बार एक मान्य बहुपद अभिव्यक्ति प्रदान की गई है, तो आप नीचे दिए गए बटन पर क्लिक कर सकते हैं, "गणना" बटन, और प्रक्रिया के सभी आवश्यक चरण दिखाए जाएंगे।

फ्रैक्चर बीजगणित में अंश रूपांतरण शामिल होता है जैसे कि आम भाजक का उपयोग, और बुनियादी अंकगणितीय नियमों का उपयोग।सभी में, गणना की प्रक्रिया श्रमसाध्य हो सकती है, हालांकि यह व्यवस्थित रूप से किया जा सकता है, बिना किसी समस्या के।

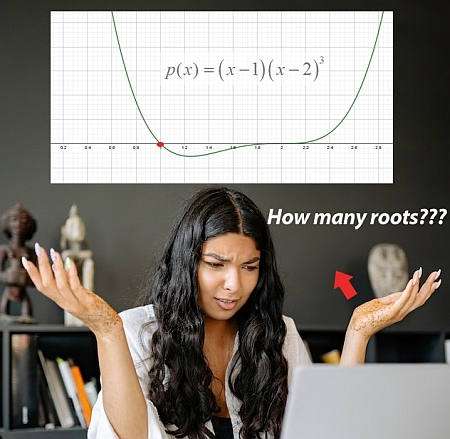
एक बहुपद कार्य क्या है?

बहुपद, सबसे सरल स्पष्टीकरण में, ऐसे कार्य हैं जो केवल \(x\) की शक्तियों से मिलकर बनते हैं, संभवतः संख्यात्मक स्थिरांक द्वारा गुणा किया जाता है, जो कि जोड़े (या घटाया) togheter हैं।उदाहरण के लिए, \(p(x) = x^3 + 2x^2 + 1\) एक बहुपद कार्य है, क्योंकि इसमें \(x\) स्थिरांक द्वारा गुणा की गई शक्तियां शामिल हैं, एक साथ जोड़ा गया।इस मामले में, \(1 = x^0\) तो एक निरंतरता भी \(x\) की शक्ति है।:

सामान्य तौर पर, एक बहुपद समारोह में निम्नलिखित रूप होता है:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

\(a_n \ne 0\) के साथ।इस मामले में, हम कहते हैं कि बहुपद की t डिगthirी (या इसका आदेश) \(n\) है, जो बहुपद समारोह में मौजूद उच्चतम शक्ति है।

इसके अलावा, गुणांक \(a_n\) कहा जाता है अफ़सीर , और \(a_n x^n\) कहा जाता है अफ़रप ।अग्रणी गुणांक और एक बहुपद की डिग्री इसके अंतिम व्यवहार को निर्धारित करेगी (यह, व्यवहार जब x का निरपेक्ष मूल्य बड़ा है)।

बहुपद समारोह के साथ काम करने के लिए क्या कदम हैं?

• Letsunt 1: स्पष्ट रूप से उस अभिव्यक्ति को पहचानें, जिसके साथ आप काम करना चाहते हैं, विस्तार करें और सरल करें
• Therur the: जांचें कि क्या वे शब्द जो चर x को शामिल करते हैं, केवल x की शक्तियों के अनुरूप हैं, अन्यथा आप रुक जाते हैं, यह एक बहुपद नहीं है
• Theirण 3: सुनिश्चित करें कि x की सभी शक्तियां स्थिरांक (जो '1' हो सकती हैं) से गुणा की जाती हैं, और वे शब्द अभिव्यक्ति में जोड़े या घटाए गए दिखाई देते हैं

यह सुनिश्चित करना महत्वपूर्ण है कि आपके पास एक बहुपद कार्य है, इसलिए आप यह सुनिश्चित कर सकते हैं कि आप ऐसे परिणाम लागू कर सकते हैं जो बहुपद के लिए अनन्य हैं, जैसे कि ए तमाम , प rayrमेय r औry तड़प ।

इसके अलावा, बहुपद कार्यों से निपटने का लाभ यह है कि आप आसानी से आचरण कर सकते हैं अँगुला या तो उपयोग करके तमाम , या अफ़रप मामले में भाजक रैखिक है।

क्या कोई महत्वपूर्ण बहुपद कार्य हैं?

वास्तव में।डिग्री 2 के कुख्यात बहुपद हैं, जिन्हें हम कहते हैं तमाम , जो बुनियादी बीजगणित में बड़े पैमाने पर अध्ययन किया जाता है।इसका कारण यह है कि सटीक सूत्रों का उपयोग करके उनका पूरी तरह से विश्लेषण किया जा सकता है।उदाहरण के लिए, आपके पास ए सराफ्यूल , और प्रसिद्ध द्विघात सूत्र का उपयोग जड़ों को खोजने के लिए किया जाता है तमाम :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

डिग्री 2 के बहुपद भी हैं, जिन्हें हम कहते हैं कmun बहुपद बहुपद , जिसमें स्पष्ट सूत्र भी होते हैं, लेकिन यह आमतौर पर अधिक जटिल माना जाता है, और आमतौर पर बुनियादी बीजगणित पाठ्यक्रमों में कवर नहीं किया जाता है।

मुझे एक बहुपद के अंतिम व्यवहार के बारे में क्या पता है?

एक बहुपद का अंतिम व्यवहार अंततः बहुपद पर निर्भर करेगा, लेकिन कुछ बातें उनकी डिग्री के आधार पर कही जा सकती हैं

• Letsunt 1: द्विघात बहुपदों के लिए, ग्राफ ऊपर की ओर खुलता है (यदि प्रमुख गुणांक सकारात्मक है) या नीचे की ओर (यदि प्रमुख गुणांक नकारात्मक है), और फ़ंक्शन दोनों पक्षों पर अनंत या माइनस अनंतता (प्रमुख गुणांक के संकेत पर निर्भर करता है) में परिवर्तित हो जाता है
• तथ २: २: डिग्री के साथ बहुपद के लिए जो विषम है (उदाहरण के लिए, डिग्री 3 के साथ) में कम से कम एक वास्तविक जड़ होगी, और फ़ंक्शन एक तरफ अनंत में परिवर्तित होता है, और दूसरी तरफ माइनस अनंतता में
• Lettum 3: डिग्री के साथ बहुपद के लिए, यहां तक कि (उदाहरण के लिए, डिग्री 4 के साथ), आवश्यक रूप से वास्तविक जड़ें नहीं होंगी (एक बिंदु जो वह ग्राफ को एक्स-एक्सिस में पार करता है), और फ़ंक्शन अनंत या माइनस इन्फिनिटी में परिवर्तित हो जाता है (इस पर निर्भर करता हैदोनों तरफ अग्रणी गुणांक का संकेत)

इसलिए, बहुपद x के बड़े मूल्यों के लिए बड़े चलते हैं, और क्या उनके मूल्य सकारात्मक या नकारात्मक हैं जो एक्स के सकारात्मक के लिए (उनके अंत व्यवहार में) प्रमुख गुणांक के संकेत पर निर्भर करते हैं।

टिप्स: एक बहुपद कार्यों का उपयोग करने के क्या लाभ हैं

बहुपद कैलकुलेटर यह सुनिश्चित कर सकते हैं कि आप सही उत्तर पर पहुंच रहे हैं।वास्तव में, अफ़रोट जटिल नहीं हैं, लेकिन वे बोझिल हो सकते हैं और गलतियाँ करना मुश्किल नहीं है।

यह सुनिश्चित करके बीजगणितीय गलतियों से बचें कि आप इस कैलकुलेटर के साथ अपने काम की जांच कर रहे हैं, ताकि आप अंतिम उत्तर की स्थिरता और वहां पहुंचने के लिए उपयोग किए जाने वाले चरणों को सुनिश्चित कर सकें।

उदाहरण: बहुपद कार्य

निम्नलिखित बहुपद समारोह की गणना करें \((x-3)(x-1)(x-4)\)

तमाम: हमें निम्नलिखित बहुपद अभिव्यक्ति के साथ प्रदान किया जाता है, जिसकी हमें गणना करने की आवश्यकता है: \(\displaystyle (x-3)(x-1)(x-4)\)।

निम्नलिखित गणना प्राप्त की जाती है:

जो बहुपद सरलीकरण की प्रक्रिया का समापन करता है।

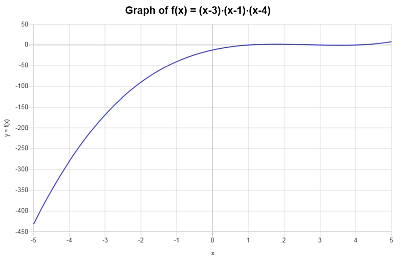
निम्नलिखित भूखंड \(\displaystyle x^3-8x^2+19x-12\) के लिए प्राप्त किया जाता है अंतराल पर \([-5, 5]\):

उदाहरण: बहुपद कार्य गणना

क्या यह एक बहुपद कार्य है: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

समाधान:

हमें निम्नलिखित बहुपद अभिव्यक्ति के साथ प्रदान किया जाता है, जिसकी हमें गणना करने की आवश्यकता है: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)।

निम्नलिखित गणना प्राप्त की जाती है:

जो सरलीकरण प्रक्रिया को समाप्त करता है।

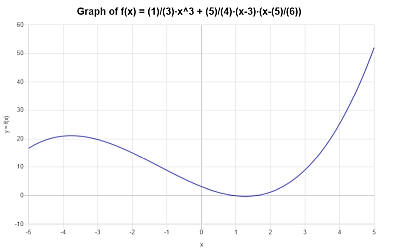
ग्राफिक रूप से, निम्नलिखित सरलीकृत फ़ंक्शन के लिए प्राप्त किया जाता है \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) अंतराल पर \([-5, 5]\):

उदाहरण: एक बहुपद कैलकुलेटर का उपयोग करना

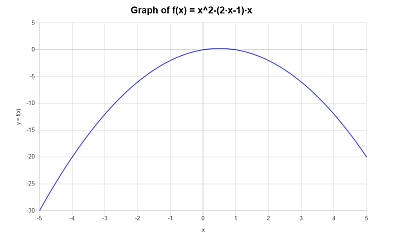
गणना \( x^2 - (2x - 1)x \)।

तमाम: इस अंतिम उदाहरण में हमारे पास \(\displaystyle x^2 - (2x - 1)x \) है, जिसे हमें सरल बनाने की आवश्यकता है।

निम्नलिखित गणना प्राप्त की जाती है:

जो सरलीकरण को समाप्त करता है।

निम्नलिखित भूखंड \(\displaystyle -x^2+x\) के लिए प्राप्त किया जाता है अंतराल पर \([-5, 5]\):

अधिक बीजगणित कैलकुलेटर

बहुपद कार्य शाब्दिक रूप से बीजगणित में केंद्र का टुकड़ा है।बुनियादी अनुप्रयोगों के लिए, तमाम एक महत्वपूर्ण भूमिका और अर्थशास्त्र, भौतिकी और इंजीनियरिंग खेलेंगे।

बहुपद कार्यों में बेहद शक्तिशाली गुण होते हैं, विशेष रूप से की गणना को शामिल करते हैं बहुपद जड़ें , जिसका अनुप्रयोगों में एक मजबूत अर्थ है।