Problème: Le résultat suivant a été fourni, qui résume les résultats d'un régression entreprise sur des échantillons appariés de sociétés britanniques en faillite et non défaillantes cotées en bourse. Les variables indépendantes utilisées sont les suivantes:

PBTCL_1 est le bénéfice avant impôts divisé par les passifs courants.

CLTA_1 correspond au passif courant par rapport au total de l'actif.

NCI_1 est l'intervalle sans crédit qui mesure la durée (en jours) pendant laquelle une entreprise peut continuer à négocier sans générer de revenus.

CATL_1 représente l'actif à court terme par rapport au total du passif.

Tous ces éléments sont calculés à partir des données issues des derniers comptes publiés avant l'échec.

La variable dépendante est dichotomique, les entreprises défaillantes étant attribuées 1 et les entreprises non défaillantes 0.

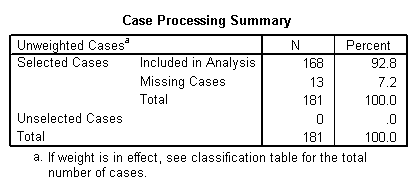
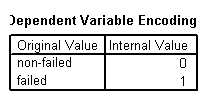
Bloc 0: bloc de début

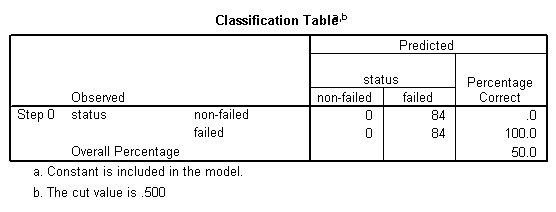
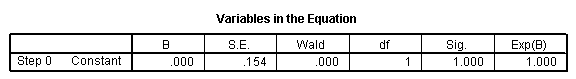
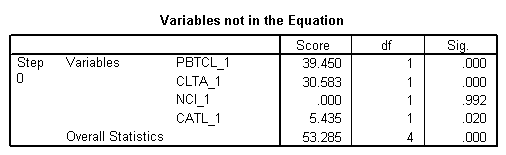
Bloc 1: Méthode = Entrée

Vous êtes tenu de procéder à une évaluation financière et statistique de ces informations.

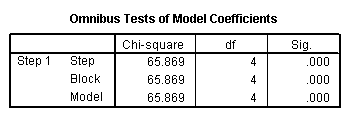
Solution: Observez que le modèle logistique est globalement significatif, p = .000. En outre, on constate que Nagelkerke R Square = 0,432, ce qui indique une qualité d'ajustement relativement acceptable pour ce modèle.

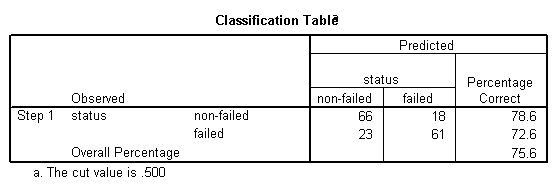
On observe que parmi les entreprises non défaillantes, 78,6% d'entre elles étaient correctement classées, tandis que parmi les entreprises défaillantes, 72,6% d'entre elles étaient correctement classées, ce qui représente un total de 75,6% d'entreprises correctement classées dans l'ensemble, ce qui indique un taux de classification relativement bon.

Le modèle logistique est

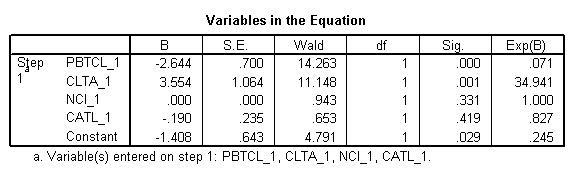
\[\ln \left( \frac{{\hat{p}}}{1-\hat{p}} \right)=-1.408-2.644*PBTCL\_1+3.554*CLTA\_1+0.000*NCI\_1-0.190*CATL\_1\]

où \(\hat{p}\) correspond à la conversation de faillite d'une entreprise. D'un point de vue financier, nous avons les conclusions suivantes:

· Pour une augmentation de 1 point du résultat avant impôt divisé par les passifs courants, les probabilités d'échec diminuent de 92,9%. Ce changement est significatif, p = 0,000 <0,05

· Pour une augmentation de 1 point du passif courant par rapport au total de l'actif, la probabilité de défaillance augmente de 3294,10% Ce changement est significatif, p = 0,001 <0,05

· Pour une augmentation d'un jour de l'intervalle sans crédit, les chances d'échec ne changent pas. Ce coefficient n'est pas significatif, p = 0,331> 0,05

· Pour une augmentation de 1 point des actifs courants par rapport au total des passifs, les probabilités de défaillance diminuent de 17,3% (cette diminution est significative, p = 0,029 <0,05)