Estatisticas Tutoriais

Tutorial ANOVA

No tutorial desta semana, vamos cobrir o tópico de Análise de variação . Veja abaixo uma lista de exemplos de problemas relevantes, com soluções passo a passo.

Esperamos que você os ache úteis. Compartilhamos tutoriais completos, dicas e sugestões, com os membros de nossa comunidade. Por favor, não hesite em Entre em contato se você tiver alguma dúvida.

Problemas de amostra de ANOVA

Questão 1: Uma análise de variância foi usada para avaliar as diferenças médias de medidas repetidas pesquisa. Os resultados foram relatados como F (3,24) = 6,40.

uma. Quantas condições de tratamento foram comparadas no estudo?

b. Quantas pessoas participaram do estudo?

Solução: (a) Havia 3 + 1 = 4 condições de tratamento.

(b) O número total de desejado é 3 + 24 + 1 = 28.

Questão 2: Os dados a seguir representam os resultados de um estudo de medidas independentes comparando três tratamentos.

uma. Calcule SS para o conjunto de 3 meios de tratamento. (Use as três médias como um conjunto de n = 3 pontuações e calcule SS.)

b. Usando o resultado da parte a, calcule n (SS significa). Observe que esse valor é igual a SS entre (consulte a Equação 13.6).

c. Agora, calcule o centro com uma fórmula computacional usando os valores T (Equação 13.7). Você deve obter o mesmo resultado da parte b.

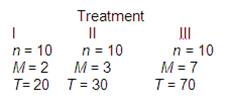
Solução: (a) Nós entendemos que \(\bar{M}=\frac{2+3+7}{3}=4\)

o que significa que

\[S{{S}_{Means}}={{\left( 2-4 \right)}^{2}}+{{\left( 3-4 \right)}^{2}}+{{\left( 7-4 \right)}^{2}}=4+1+9=14\]

(b) Isso implica que \(n*S{{S}_{Means}}=10\times 14=140\).

\[S{{S}_{Between}}=\frac{{{20}^{2}}}{10}+\frac{{{30}^{2}}}{10}+\frac{{{70}^{2}}}{10}-\frac{{{120}^{2}}}{30}=140\]

Questão 3: Os danos às residências causados pelo rompimento da tubulação podem ser caros para consertar. Quando o vazamento para descoberto, centenas de litros de água podem já ter inundado a casa. As válvulas de desligamento automático podem evitar danos extensos causados pela água devido a falhas no encanamento. As válvulas sensores sensores que interrompem o fluxo de água em caso de vazamento, evitando inundações. Uma característica importante é o ritmo (em milissegundos) necessário para o sensor detectar o vazamento de água. Os dados de amostra coletados para quatro válvulas de corte diferentes estão contidos no arquivo Waterflow.

uma. Produza a tabela ANOVA relevante e conduza um teste de hipótese para determinar se o tempo médio de detecção difere entre os quatro modelos de válvula de corte. Use um nível de significância de 0,05.
b. Qual é a fonte de variação entre os fundadores?

Válvula 1	Válvula 2	Válvula 3	Válvula 4
17	18	28	17
10	17	25	17
18	11	30	17
18	16	26	19
17	16	25	18
14	18	27	21
18	14	23	21
13	17	23	12
10	20	26	15
11	14	22	18

Solução: A tabela a seguir é obtida a partir dos dados fornecidos

Obs.	Válvula 1	Válvula 2	Válvula 3	Válvula 4
	17	18	28	17
	10	17	25	17
	18	11	30	17
	18	16	26	19
	17	16	25	18
	14	18	27	21
	18	14	23	21
	13	17	23	12
	10	20	26	15
	11	14	22	18

Significar	14,6	16,1	25,5	17,5
St. Dev.	3.406	2.558	2.461	2.677

Nós gostaríamos de testar

\[H_0: \,\mu_{1}= \mu_{2}= \mu_{3}= \mu_{4}\]

\[H_A: \operatorname{Not all the means are equal}\]

Com os dados encontrados na tabela acima, podemos calcular os seguintes valores, que são necessários para construir a tabela ANOVA. Nós temos:

\[SS_{Between}=\sum\limits_{i=1}^{k}{n}_{i} {\left( {\bar{x}}_{i}-\bar{\bar{x}} \right)}^{2}\]

and therefore

\[SS_{Between}={10}\left({14.6}-{18.425}\right)^2+ {10}\left({16.1}-{18.425}\right)^2+ {10}\left({25.5}-{18.425}\right)^2+ {10}\left({17.5}-{18.425}\right)^2=709.475\]

Also,

\[SS_{Within} = \sum\limits_{i=1}^{k}{\left( {n}_{i}-1 \right) s_{i}^{2}}\]

de onde nós temos

\[SS_{Within}=\left({10}-1\right) \times {3.406}^2+ \left({10}-1\right) \times {2.558}^2+ \left({10}-1\right) \times {2.461}^2+ \left({10}-1\right) \times {2.677}^2=282.3\]

Therefore

\[MS_{Between}=\frac{SS_{Between}}{k-1}= \frac{{709.475}}{3}= {236.492}\]

Da mesma forma, consegue-se que

\[MS_{Within} = \frac{SS_{Within}}{N-k}= \frac{{282.3}}{36}= {7.842}\]

Portanto, a estatística F é calculada como

\[F=\frac{MS_{Between}}{MS_{Within}} = \frac{{236.492}}{{7.842}}= {30.1583}\]

O valor crítico para \(\alpha ={0.05}\), \(df_{1} = 3\) e \(df_{2}= {36}\) é dado por

\[F_C = {2.8663}\]

e o valor p correspondente é

\[p=\Pr \left( {{F}_{3,36}}> {30.1583} \right) = {0.000}\]

Observa-se que o valor de p é menor que o nível de significância \[\alpha =0.05\] e, consequentemente, rejeitamos \({{H}_{0}}\). Consequentemente, temos evidências suficientes para rejeitar a hipótese nula de médias iguais, ao nível de significância de 0,05.

Resumindo, temos a seguinte tabela ANOVA: