Этот калькулятор формулы вершины

Данный калькулятор позволит применить формула вершины для заданной квадратичной функции, которую вы предоставите. Эта квадратичная функция должна быть действительной, например, 2x^2 + 3x + 1/3, или она может быть не упрощенной, например, 2x^2 - x + 5 - 3/4 x^2 +1/3 и т.д. Подойдет любая действительная действительная квадратичная функция.

После того как вы зададите действительную квадратичную функцию, нужно нажать кнопку "Вычислить", после чего будут показаны шаги применения формулы вершины с последующими шагами для вычисления вершины параболы.

Квадратичные функции действительно важны в приложениях к алгебре и исчислению, а вершина квадратичной функции очень хорошо поддается интерпретации.

Что такое формула вершины?

Во-первых, мы предполагаем, что начинаем с квадратичной функции и упростили ее до:

\[ f(x) = ax^2 + bx + c \]

Тогда формула вершины для координаты x вершины имеет вид:

\[ x_V = \displaystyle -\frac{b}{2a}\]

Как применить формулу вершин?

• Шаг 1: Определите квадратичную функцию в ее упрощенной форме. У вас должно быть что-то вроде f(x) = ax²+ bx + c
• Шаг 2: Из квадратичной формулы нужно четко определить, что такое a и b
• Шаг 3: Из определенных вами a и b подставьте их в формулу xv = -b/2a

Обратите внимание, что если a = 0, то формула будет неопределенной, но в данном случае a не будет нулем, так как у нас квадратичная функция, а член, который умножает x², не может быть нулем, чтобы быть действительной квадратичной функцией.

Почему важно найти вершину?

Вершина обладает очень важным свойством - это точка, в которой квадратичная функция достигает минимума (когда она раскрывается вверх при a > 0) или точка, в которой квадратичная функция достигает максимума (когда она раскрывается вниз при a > 0).

Таким образом, при нахождении вершины мы уже получаем экстремальную точку квадратичной функции.

Пример: вычислить вершину

Вычислите вершину для следующей квадратичной функции: \(f(x) = 3x^2+3x+2\)

Отвечать: Нам нужно найти координаты вершины квадратичной функции \(f(x) = \displaystyle 3x^2+3x+2\).

Для квадратичной функции вида \(f(x) = a x^2 + bx + c\) координата x вершины вычисляется по следующей формуле:

\[x_V = \displaystyle -\frac{b}{2a}\]

В этом случае мы имеем, что функция, для которой нам нужно найти вершину, равна \(f(x) = \displaystyle 3x^2+3x+2\), из чего следует, что соответствующие коэффициенты являются:

\[a = 3\] \[b = 3\] \[c = 2\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{1}{2}\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{1}{2}\), а координата y вершины равна \(y_V = \displaystyle \frac{5}{4}\). Таким образом, точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

Графически получается следующее:

Пример: применение вершинной формулы

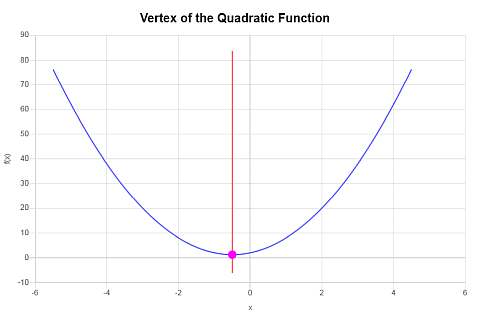
Используйте формулу вершины для вычисления координат вершины, связанной с функцией \(f(x) = x^2 + 4x - \frac{3}{4}\)

Отвечать: Опять же, мы используем следующую формулу:

\[x_V = \displaystyle -\frac{b}{2a}\]

Поскольку \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), из чего следует, что соответствующие коэффициенты:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -2\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -2\), а координата y вершины равна \(y_V = \displaystyle -\frac{19}{4}\). Таким образом, точка, обозначающая вершину, равна \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

На этом расчеты завершены.

Пример: применение вершин

Найдите точку экстремума функции \(f(x) = -2x^2 - 3x + 5\). Является ли эта точка экстремума точкой минимума или максимума?

Отвечать: Нам нужно найти координаты вершины квадратичной функции \(f(x) = \displaystyle -2x^2-3x+5\).

Мы используем следующую формулу:

\[x_V = \displaystyle -\frac{b}{2a}\]

В данном случае мы имеем, что функция, для которой нам нужно найти вершину - \(f(x) = \displaystyle -2x^2-3x+5\), тогда:

\[a = -2\] \[b = -3\]

Это означает, что:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{3}{4}\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{3}{4}\), а координата y вершины равна \(y_V = \displaystyle \frac{49}{8}\). Таким образом, точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Обратите внимание, что \(a = -2 < 0\), тогда парабола раскрывается вниз, а точка \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) соответствует точке максимума. То есть квадратичная функция \(f(x) = \displaystyle -2x^2-3x+5\) достигает максимума \( \displaystyle \frac{49}{8}\) в точке \( x = -\frac{3}{4}\)

Больше квадратичных калькуляторов

С квадратичными функциями можно сделать многое. Вы можете вычислить корни квадратного уравнения вы можете найти ось симметрии квадратичной функции, и так далее, и так далее.

Применение формула вершины тесно связана с применением квадратичная формула и Ось симметрии .