Подробнее о квадратных неравенствах

Этот расчет квадратного неравенства предоставит вам решения неравенств с указанием всех шагов. Например, предоставленное вами неравенство может выглядеть примерно так: "x^2 - 1/2 > 0", и, как правило, квадратичные неравенства решить не так уж и сложно.

Как только вы предоставите действительное неравенство, включающее квадратичное выражение , вы можете нажать "Рассчитать", чтобы получить все показанные вам этапы расчета, включая график решений неравенства.

квадратичные неравенства являются одним из немногих типов (наряду с линейные неравенства ), что вы гарантированно сможете найти точное решение, и этот процесс предполагает решение квадратного уравнения.

Каково определение этого вида неравенства?

Мы не заявляли об этом явно, но из названия ясно следует: квадратное неравенство — это особый тип неравенства, в котором все члены, входящие в него, являются полиномами не выше 2-й степени. В этом контексте одним из примеров является

\[\displaystyle x^2 < x - 1\]

которое является квадратичным в силу того, что обе части неравенства являются полиномами порядка не выше 2. Теперь, если бы у вас было:

\[\displaystyle x^2 < x^3 - 1\]

тогда неравенство больше не является квадратичным из-за члена \(x^3\) в правой части. Для этих неравенств у нас есть четкая дорожная карта для поиска решения.

Шаги по решению квадратичных неравенств

• Шаг 1: Убедитесь, что перед вами квадратное неравенство, так как используемый в этом случае метод справедлив только для этого типа неравенства
• Шаг 2: Как и в большинстве неравенств, передайте все в левую часть неравенства и решите соответствующее уравнение
• Шаг 3: Если соответствующее квадратное уравнение не имеет действительных корней, мы знаем, что либо вся действительная прямая является решением, либо решения нет. Итак, вы проверяете любую точку и смотрите, решает ли она неравенство, и если да, то решением является вся действительная линия (-∞, ∞), в противном случае решение пусто.
• Шаг 4: Если связанное квадратное уравнение имеет только одно действительное решение, это означает, что соответствующий квадратичный график касается оси x по касательной. Таким образом, в зависимости от знака неравенства у вас может быть только точка касания, являющаяся решением, или все, кроме точки касания, являющееся решением, или вся действительная линия (-∞, ∞), для которой вам нужно проверить точку касания, и точка вне этого (слева и справа от точки)
• Шаг 4: Если связанное квадратное уравнение имеет два разных действительных решения, вы проверяете интервалы, определенные этими корнями, чтобы определить, какие части вещественной линии будут частью решения

После анализа частей, при необходимости, вы объединяете их с помощью оператора "объединения", который используется для объединения интервалов.

Как нарисовать квадратное неравенство?

Графическое отображение неравенств предоставляет отличный способ визуально понять, как выглядит решение. С точки зрения процедуры вам необходимо знать, работаете ли вы с неравенством с одной переменной или у вас больше переменных.

Если у вас есть неравенство, например

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

у вас есть только одна переменная, и тогда решением будет подмножество реальной строки. С другой стороны, если у вас было что-то вроде

\[\displaystyle y < x^2 - \frac{1}{2} x \]

тогда у вас есть только две переменные x и y, и тогда решение неравенства будет подмножеством плоскости xy.

Важность квадратных выражений

Квадратные выражения, входящие в уравнения и неравенства, играют фундаментальную роль в математике. Пожалуй, квадратичная структура является наиболее широко используемым типом структуры после линейной.

Занимаясь исчислением и алгеброй, вы найдете бесчисленное множество применений квадратичных уравнений в задачах максимизации и минимизации, интегрирования и многого другого. Немного покопавшись, вы найдете применение квадратичных выражений в различных научных дисциплинах

Пример: квадратные неравенства

Решите это квадратное неравенство: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Решение:

Сначала нам нужно решить следующее вспомогательное квадратное уравнение \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Применение квадратичной формулы

Квадратное уравнение:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В этом случае мы имеем:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Подставив эти значения в формулу для корней, получим:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

итак, мы выяснили, что:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Критические точки

Список обнаруженных критических точек организован в порядке возрастания: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Затем нам необходимо проанализировать следующие критические интервалы:

• Для интервала \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): левая часть положительна, поэтому \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) не является частью решения.

• Для интервала \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): левая часть отрицательна, что означает, что \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) является частью решения.

• Для интервала \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): левая часть положительна, что означает, что \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) не является частью решения.

Решение

На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Используя интервальную запись, решение записывается как:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]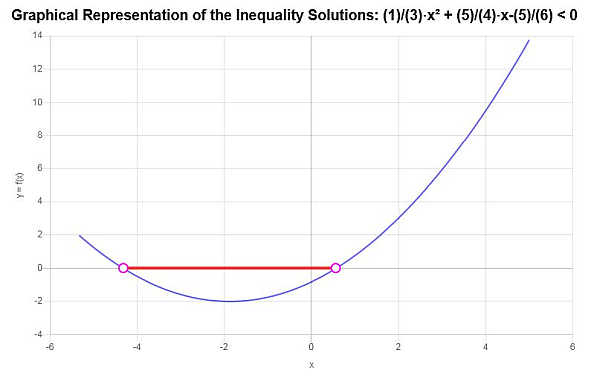

Пример: дополнительные квадратичные неравенства

Решите: \(x^2 < 4\)

Решение:

Данное неравенство:

\[x^2 < 4\]

которое выводится из квадратного уравнения \(\displaystyle x^2-4=0\).

Квадратичная формула

Для квадратного уравнения формы \(a x^2 + bx + c = 0\) корни вычисляются с использованием следующей формулы: квадратичная формула :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В этом случае нам нужно решить уравнение \(\displaystyle x^2-4 = 0\), что означает, что соответствующие коэффициенты:

\[a = 1\] \[b = 0\] \[c = -4\]

Сначала мы вычислим дискриминант, чтобы оценить природу корней. Дискриминант вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Поскольку в этом случае мы получаем дискриминант \(\Delta = \displaystyle 16 > 0\), который является положительным, мы знаем, что уравнение имеет два разных действительных корня.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

итак, мы выяснили, что:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

В этом случае квадратное уравнение \( \displaystyle x^2-4 = 0 \) имеет два действительных корня, поэтому:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

тогда исходный полином факторизуется как \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), что завершает факторизацию.

Анализ критических точек

Список обнаруженных критических точек организован в порядке возрастания: \(-2\), \(2\).

Исходя из этого, нам необходимо проанализировать следующие интервалы:

• Для интервала \(\left(-\infty, -2\right)\): левая часть положительна, поэтому \(\left(-\infty, -2\right)\) не является частью решения.

• Для интервала \(\left(-2, 2\right)\): левая часть отрицательна, поэтому \(\left(-2, 2\right)\) является частью решения.

• Для интервала \(\left(2, \infty\right)\): левая часть положительна, что означает, что \(\left(2, \infty\right)\) не является частью решения.

Решение неравенства

На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(-2< x \le 2\).

Используя интервальную запись, решение записывается как:

\[\left[-2,2\right)\]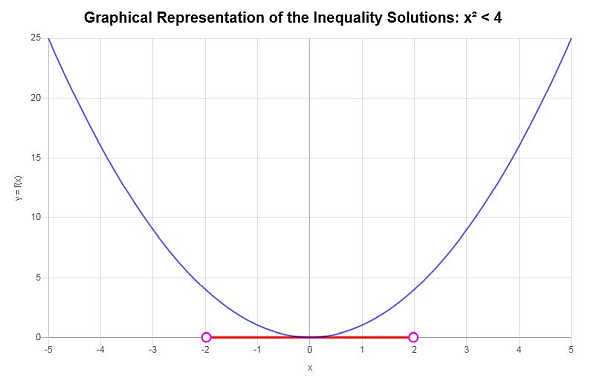

Другие полезные калькуляторы неравенства

Самый простой тип неравенства, который вы сможете решить, — это линейные неравенства . После этого у вас есть квадратные неравенства, с точки зрения простоты.

Тогда у вас есть полиномиальные неравенства в общем, со степенью выше 2. Это должны быть простые задачи, но они все равно могут быть огромными задачами с точки зрения объема кропотливой работы, необходимой для их решения.

Имея калькулятор неравенства ибо неравенства вообще могут действительно пригодиться, так как будут касаться разных типов неравенств, поддающихся поиску точных решений.