Калькулятор неравенства
Инструкции: Используйте калькулятор неравенства, чтобы решить любое указанное вами неравенство, показывая все шаги. Пожалуйста, введите неравенство, которое вы хотите решить, в поле ниже:
Подробнее о решении неравенств
С помощью этого калькулятора вы сможете решать предложенные вами неравенства. Все, что вам нужно сделать, это ввести желаемое неравенство в поле, а также убедиться, что вы указываете допустимое неравенство.
Например, вы можете указать что-то вроде "2x^2 - x >= 1/2" или что-то вроде "sin(x) > 0", если вы предоставите действительные значения. Также убедитесь, что вы используете знак неравенства, например ">", "<", ">=" или "<=".
Если вместо этого вы используете "=", то этот калькулятор будет действовать как калькулятор уравнений .
После того, как вы предоставите действительное неравенство, следующим шагом будет нажатие кнопки "Решить", и через долю секунды вам будет представлено пошаговое решение. Одно предостережение: не все неравенства удастся решить, так что имейте это в виду.
Не все неравенства легко решить, и мы не можем применить некоторые предвзятые методы. Лишь некоторые виды, например линейные неравенства , квадратичные неравенства или полиномиальные равенства (для низших степеней) допускают систематическое лечение.

Что такое неравенство?
Неравенство — это тип математического объекта, который очень похож на математическое уравнение , с той разницей, что вместо "=" неравенство содержит либо ">", "<", ">=" или "<=". Эта небольшая разница во внешнем виде по-прежнему усложняет решение неравенства, чем уравнения.
Например, выражение ниже представляет собой неравенство
\[\displaystyle x + \frac{1}{3} < x^2 \]Итак, это математическое выражение, которое имеет две части: левую и правую, и имеет "<" в качестве соответствующего знака неравенства. Приведенное выше неравенство называется квадратным неравенством, поскольку выражения в левой и правой частях являются полиномиальными, а высшая степень равна 2.
Например, приведенное ниже неравенство является тригонометрическим неравенством:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]Это неравенство, поскольку оно имеет знак неравенства \(\le\), а в правой части стоит знак неравенства тригонометрическое выражение . Заметьте, что первое неравенство решить довольно просто, тогда как другое далеко не так просто, и вы фактически не можете его решить.
Как решить неравенство
В общих чертах, мы найдем решение неравенства, решив сначала соответствующее уравнение. Решить неравенство будет сложнее, чем сложнее решить связанное с ним уравнение. Следующие шаги помогут вам в процессе решения:
- Шаг 0: Упростите выражения участвует в неравенстве. Почти всегда легче решить упрощенное неравенство, чем исходное
- Шаг 1: Определите неравенство, которое вы хотите решить, и внимательно определите знак неравенства (>, ≥, <, ≤). Если у вас есть "=", вам следует использовать калькулятор уравнений вместо
- Шаг 2: Затем вы записываете связанное уравнение, которое просто получается путем замены знака неравенства, найденного на предыдущем шаге, а затем замены его знаком равенства "="
- Шаг 3: Решите связанное уравнение. Вы определите решение неравенства, основываясь на существовании реальных решений связанного с вами уравнения и делая заметки обо всех моментах, которые могут сделать выражение неопределенным
- Шаг 4: Если связанное с вами уравнение не имеет реального решения: в этом случае вы знаете, что уравнение никогда не равно нулю, по крайней мере, для действительных значений. Тогда, при условии непрерывности, либо все точки являются решением неравенства, либо ни одна из них не является решением неравенства. Таким образом, вы оцениваете неравенство в любой точке (скажем, x = 0), и если оно выполняется, то все действительные значения являются решением неравенства, а если нет, то реальных решений нет
- Шаг 5: Наконец, предположим, что существуют действительные решения соответствующего уравнения. Мы назовем эти критические точки и добавим любые точки, в которых выражение становится неопределенным (деление на ноль и т. д.), в список критических точек
- Шаг 6: Если есть только одна критическая точка, которую мы называем "а": оцените неравенство в любой точке слева от "а", и если оно выполняется, интервал (-∞, а) будет частью набора решений. Если неравенство равно "<=" или ">=", то вы включаете конечную точку Наконец (-∞, a). Вы делаете аналогичный шаг для точки справа от "a", и если для нее выполняется неравенство, то (-∞, a) будет частью множества решений
- Шаг 7: Аналогичный процесс выполняется, если существует более одной критической точки: возьмите две последовательные критические точки, которые мы называем "a1" и "a2": оцените неравенство в любой точке между a1 и a2, и, если оно выполняется, интервал ( a1, a2) будет частью множества решений. Если неравенство "<=" или ">=", то вы включаете конечные точки
Это кажется сложным, но нужно просто быть системным. Например, если ваше неравенство — \(\displaystyle x + \frac{1}{3} < x^2 \), то связанное с ним уравнение — \(\displaystyle x + \frac{1}{3} = x^2 \), которое легко решить, поскольку оно является Квадратное уравнение .
Затем, в контексте анализа критических точек (если таковые имеются), построение графика решения неравенства может внести ясность. На некоторых уроках алгебры учащихся учат использовать таблицы, чтобы отслеживать, что происходит между критическими точками, что может быть действительно полезно.
В чем отличие от системы неравенств?
Система неравенств состоит из нескольких одновременных неравенств, которые необходимо решать одновременно. Это звучит сложнее, чем решение простого неравенства, потому что это сложнее. Если решение неравенств может быть трудоемким, тем более для системы неравенств.
Пример системы неравенств показан ниже:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]В приведенном выше примере у вас есть система неравенств быть решенным. Эта система неравенств имеет два неравенства и два неизвестных (x и y).
Как вы, наверное, понимаете, решение системы неравенств в целом может быть трудной задачей. В основном мы сосредоточимся на решении системы линейных уравнений, которые тесно связаны с решение системы линейных уравнений

Преимущества использования этого калькулятора неравенств с шагами
Действительно, решить большинство неравенств будет сложно. Лишь немногие из них, имеющие очень специфическую структуру, поддаются анализу. Большинство этого не сделает, так что вам лучше быть к этому готовым.
- Преимущество 1: Сэкономьте много времени: решение неравенств может занять много времени, так как сначала нужно решить соответствующее уравнение, а затем проанализировать критические точки
- Преимущество 2: Убедитесь, что вы приложите все усилия для его решения: как вы, вероятно, теперь знаете, не все уравнения или неравенства можно легко решить или вообще решить. Калькулятор с шагами попробует наилучший возможный подход на основе обнаруженной структуры
- Преимущество 3: Получайте результаты, шаг за шагом, аккуратно. Некоторые калькуляторы дадут вам окончательный ответ, но не покажут шаги. Также будет полезен график, изображающий решения
Пока вы изучаете основы, калькулятор неравенства, который выполняет за вас тяжелую работу, покажет вам, как все делается, и, вероятно, вы приобретете навыки, необходимые для обнаружения структур, с которыми легче справиться.
Есть ли практическая польза от неравенств?
Держу пари! В базовой математике (Алгебра и исчисление 101) больше внимания уделяется равенствам и уравнениям. Реальный мир полон процессов, где у нас не обязательно есть уравнения, но есть неравенства, которые возникают из нижней или верхней границы, налагаемой некоторыми физическими ограничениями.
Некоторые сложные области математики, такие как дифференциальные уравнения, основывают свои теоретические основы на неравенствах (которые в некоторых контекстах эксперты любят называть "оценками энергии").
Важность неравенств может быть для вас не очевидна, а необходимость их изучения не слишком очевидна, но на самом деле неравенства составляют один из краеугольных камней математической методологии, используемой для построения теорий, хотя в довольно окончательных результатах мы склонны видеть равенства. вместо.

Пример: решение неравенств
Вычислите решение: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Отвечать: Нам нужно поместить все члены неравенства в левую часть (может быть и в правую, но удобнее использовать левую):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]Из приведенного выше неравенства получаем связанное с ним линейное уравнение, которое необходимо решить в первую очередь:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Шаг 0: В этом случае нам сначала необходимо упростить данное линейное уравнение, и для этого мы проводим следующие шаги упрощения:
Решение линейного уравнения
Поместив \(x\) слева и константу справа, мы получим
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Теперь, решая \(x\), разделив обе части уравнения на \(\frac{1}{3}\), получаем следующее:
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]и упрощая окончательно получаем следующее
\[\displaystyle x=-\frac{13}{4}\]Следовательно, решение \(x\) для данного линейного уравнения приводит к \(x=-\frac{13}{4}\).
Анализ критических точек
Единственная обнаруженная критическая точка — это \(-\frac{13}{4}\).
Исходя из этого, нам необходимо проанализировать следующие интервалы:
• Для интервала \(\left(-\infty, -\frac{13}{4}\right)\): левая часть отрицательна, поэтому \(\left(-\infty, -\frac{13}{4}\right)\) не является частью решения.
• Для интервала \(\left(-\frac{13}{4}, \infty\right)\): левая часть положительна, что означает, что \(\left(-\frac{13}{4}, \infty\right)\) является частью решения.
Решение неравенства
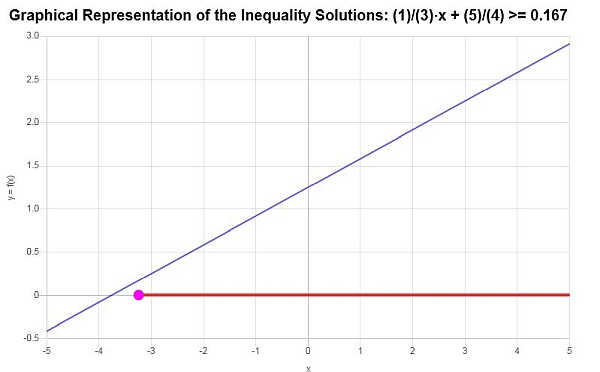
На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x \ge -\frac{13}{4}\).
Используя интервальную запись, решение записывается как:
\[\left[-\frac{13}{4},\infty\right)\]график линейного неравенства полученного решения показано ниже
Пример: еще примеры неравенства
Найдите решение следующей задачи: \(\sin(x) > 0\)
Отвечать: Нам дано следующее тригонометрическое неравенство, которое необходимо решить:
\[\sin\left(x\right) > 0\]Обработка вспомогательного уравнения
Из приведенного выше тригонометрического неравенства мы получаем связанное уравнение, которое нам нужно решить в первую очередь:
\[\sin\left(x\right)=0\]Решение вспомогательного тригонометрического уравнения
тогда решения следующие: \(x = \pi{}K\), для произвольной целочисленной константы \(K\).
Анализ критических точек
На основе решений вспомогательного уравнения найден список критических точек: \(\pi{}K\), для произвольной целочисленной константы \(K\).
Обратите внимание, что у нас бесконечное количество критических интервалов, поэтому мы проанализируем некоторые из них ниже:
• Для интервала \(\left(-3\pi{}, -2\pi{}\right)\): левая часть отрицательна, поэтому \(\left(-3\pi{}, -2\pi{}\right)\) не является частью решения.
• Для интервала \(\left(-2\pi{}, -\pi{}\right)\): левая часть положительна, что означает, что \(\left(-2\pi{}, -\pi{}\right)\) является частью решения.
• Для интервала \(\left(-\pi{}, 0\right)\): левая часть отрицательна, что означает, что \(\left(-\pi{}, 0\right)\) не является частью решения.
• Для интервала \(\left(0, \pi{}\right)\): левая часть положительна, что означает, что \(\left(0, \pi{}\right)\) является частью решения.
• Для интервала \(\left(\pi{}, 2\pi{}\right)\): левая часть отрицательна, поэтому \(\left(\pi{}, 2\pi{}\right)\) не является частью решения.
• Для интервала \(\left(2\pi{}, 3\pi{}\right)\): левая часть положительна, что означает, что \(\left(2\pi{}, 3\pi{}\right)\) является частью решения.
И так поступаем для всей последовательности интервалов.
Интервалы решения детали
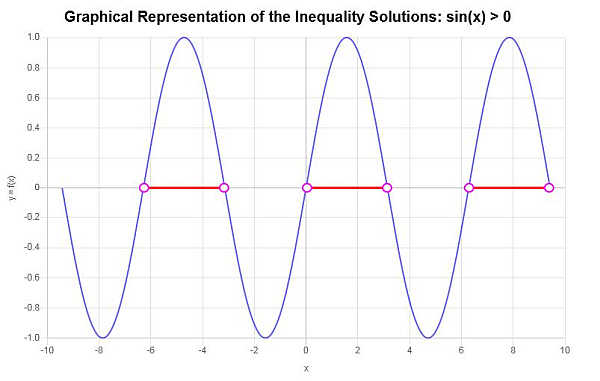
На основе анализа найденных критических точек и соответствующих интервалов, порожденных последовательными критическими точками, мы можем выделить следующее как часть решения неравенства:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]В этом случае мы можем приблизительно определить различные области решения, как показано на графике ниже график неравенства дает следующее графическое изображение найденного решения:
Пример: больше неравенств
Решить квадратное неравенство \( x^2 - 2x > 6 \).
Отвечать: Неравенство, которое нам нужно решить, это
\[x^2-2x > 6\]Сложив все члены неравенства в одну сторону, получим:
\[x^2-2x-6>0\]Вспомогательное уравнение
Получаем следующее вспомогательное уравнение, которое необходимо решить в первую очередь:
\[x^2-2x-6=0\]В левой части у нас есть полиномиальное выражение: \(\displaystyle deg(p) = 2\), его старший коэффициент — \(\displaystyle a_{2} = 1\), а постоянный коэффициент — \(\displaystyle a_0 = -6\).
Квадратичная формула
В этом случае корни вычисляются по следующей формуле:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]итак, мы выяснили, что:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]В этом случае квадратное уравнение \( \displaystyle x^2-2x-6 = 0 \) имеет два вещественных корня, которые становятся критическими точками:
Анализ критических точек
Список обнаруженных критических точек организован в порядке возрастания: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Исходя из этого, нам необходимо проанализировать следующие интервалы:
• Для интервала \(\left(-\infty, -\sqrt{7}+1\right)\): левая часть положительна, что означает, что \(\left(-\infty, -\sqrt{7}+1\right)\) является частью решения.
• Для интервала \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): левая часть отрицательна, поэтому \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) не является частью решения.
• Для интервала \(\left(\sqrt{7}+1, \infty\right)\): левая часть положительна, что означает, что \(\left(\sqrt{7}+1, \infty\right)\) является частью решения.
Находим решение неравенства
На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x < -\sqrt{7}+1\) или \(x > \sqrt{7}+1\).
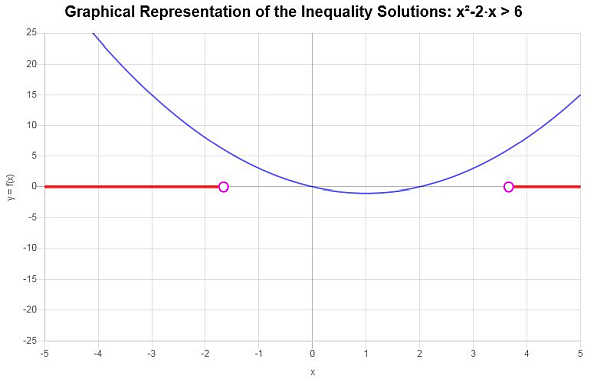
Используя интервальную запись, решение записывается как:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]Решение неравенства показано графически:
Подробнее о неравенствах выше
Вы всегда начинаете с калькулятор линейных неравенств , или, возможно, калькулятор квадратных неравенств , потому что именно они гарантированно предоставят решение.
Тогда даже с полиномиальное неравенство вы можете попасть в зыбучий песок, поскольку полиномиальные неравенства также могут оказаться сложными или даже невозможно точно решить их элементарными методами.
Любой другой тип неравенства будет зависеть от его структуры и какой-нибудь умной замены, которую вы можете придумать.




