О цепном правиле

Этот калькулятор позволит вам применять цепное правило к любой составной функции, которую вы предоставляете. А Составная функция соответствует случаю, когда вы оцениваете функцию внутри функции. Чтобы Калькулятор цепных правил работал, вам необходимо предоставить допустимую дифференцируемую составную функцию.

Одним из примеров действительной функции может быть f(x) = (sin(x))^2, где здесь у нас есть функция 'x^2', которая оценивается в другой функции, которая является sin(x), формируя составная функция.

После того, как действительная, дифференцируемая функция была предоставлена, следующее, что вам нужно сделать, это нажать на кнопку с надписью "Рассчитать", которая затем запустит вычисления, и вам будут показаны все шаги.

Производная цепного правила является одним из наиболее часто используемых правил дифференцирования. Это связано с тем, что композиция функций является одним из наиболее естественных способов построения новых функций на основе элементарных.

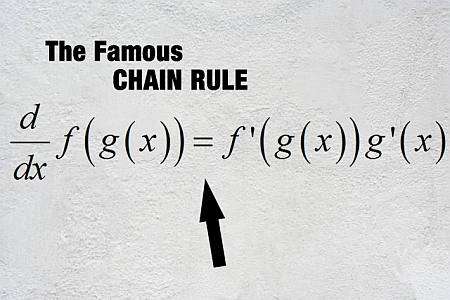
Что такое цепное правило

Проще говоря, цепное правило позволяет различать составные функции, то есть функции, вычисляемые внутри других функций. Итак, скажем, у нас есть функция \(f(x)\) и \(g(x)\), и мы знаем, как вычислить производную этих функций, то есть \(f'(x)\) и \(g'(x)\).

Тогда есть Формула цепного правила что позволяет нам вычислить производную составной функции \(f \circ g\), которая определяется как \((f \circ g)(x) = f(g(x))\):

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Шаги по использованию цепного правила

• Шаг 1: Определите внешнюю функцию f (x) и внутреннюю функцию g (x).
• Шаг 2: Убедитесь, что f(x) и g(x) являются допустимыми, дифференцируемыми функциями, и вычислите соответствующие производные f'(x) и g'(x)
• Шаг 3: Используйте формулу (f \circ g)'(x) = f'(g(x))g'(x), которая указывает, что мы оцениваем производную внешней функции по внутренней функции и умножаем ее на производную внутренней функции

Обратите внимание, как в приведенных выше шагах используется идея "внутренней" и "внешней" функции. Возможно, это не стандартный термин, а скорее идея, которая может помочь вам определить роль, которую играет каждая функция при использовании цепного правила.

Применение цепных правил

Цепное правило действительно является отличным инструментом для поиска деривативов и, как правило, является ключом к любому производный калькулятор , наряду со всеми другими основными Правила производных . Но Цепное правило имеет особую интерпретацию в том, что называется Связанные Ставки

Чтобы придать контекст идее связанных ставок, давайте начнем с формы написания цепного правила, которое, возможно, многим людям будет легче понять:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

Приведенная выше форма цепного правила гласит, что если \(y\) является функцией \(z\), а \(z\) является функцией \(x\), то в конечном счете \(y\) является функция \(x\), и вы можете найти производную от \(y\) относительно \(x\) с помощью цепного правила.

Как вы, наверное, догадались, \(y\) играет роль \(f(x)\) ("внешняя" функция), а \(z\) играет роль \(g(x)\) ("внутренняя" функция).

Приведенная выше форма Цепного правила связывает скорость изменения y по отношению к x, со скоростью изменения y по отношению к z и z по отношению к x, и, следовательно, термин "связанные скорости".

Это чрезвычайно полезно на практике. Пример: радиус круга увеличивается со скоростью 2 см/с, какова скорость изменения площади круга? Таким образом, вы можете либо пойти и выразить радиус круга как функцию t, отражая тот факт, что он увеличивается со скоростью 2 см/сек, ИЛИ вы можете использовать цепное правило.

Итак, вы называете A площадью, r радиусом и t временем. Что вам нужно вычислить, так это \(\displaystyle \frac{dA}{dt}\), поэтому вы используете цепное правило напрямую, поскольку вы знаете \(A = \pi r^2\) и r'(t) = 2, поэтому тогда

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Правило частичной производной цепи

Можно ли использовать цепное правило с частные производные ? Конечно, частичное дифференцирование точно такое же, как и обычное дифференцирование, за исключением того, что другие переменные предполагаются постоянными, поэтому обычное Правила производных применять.

Таким образом, применяется идеальное цепное правило с несколькими переменными, только одна переменная изменяется в каждый момент времени.

Интеграция цепных правил

Цепное правило в том смысле, что оно не применяется как производный инструмент, а вместо этого становится бесценным инструментом интеграции для подстановок и изменений переменных.

Его можно рассматривать как своего рода правило обратной цепи.

Пример: использование цепного правила

Вычислить производную функции: \(f(x) = \sin(\cos(x)) \)

Отвечать: Рассмотрим функцию \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\). Эта функция соответствует композиции двух функций: sin(x) и cos(x), поэтому в данном случае применяется цепное правило.

Какой вывод : Мы можем сделать вывод, что искомая производная:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

и на этом расчеты завершены.

Пример цепного правила

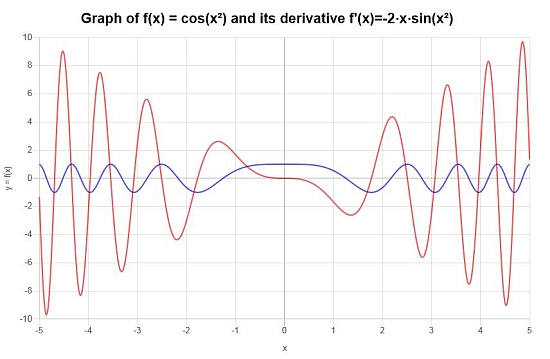
Используя цепное правило и любые другие производные правила, вычислите: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Отвечать: В этом примере у нас есть функция \(\displaystyle f(x)=\cos\left(x^2\right)\), которая соответствует сложной функции, которая указывает, что цепное правило является правильным производным правилом для начала (для вычислений потребуются другие правила).

Окончательная Производная : Вывод состоит в том, что производная предоставленной функции определяется выражением:

\[f'(x) = -2x\sin\left(x^2\right)\]

На отрезке \([-5, 5]\) можно построить следующее графическое изображение:

Пример: расчет другого правила цепочки

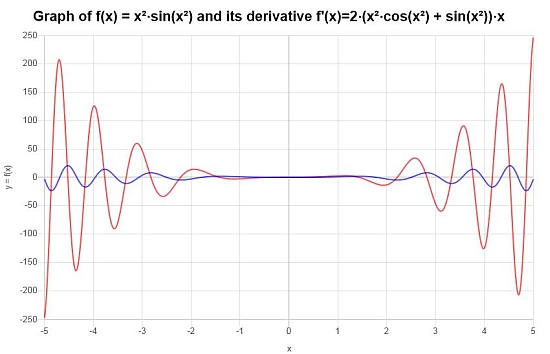
Вычислите производную \( f(x) = x^2 \sin(x^2)\) с помощью цепного правила.

Решение:

Была предоставлена следующая функция: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), для которой необходимо вычислить ее производную.

Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:

Какой окончательный вывод : Окончательный вывод состоит в том, что искомая производная определяется выражением:

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Графически имеем:

Другие производные калькуляторы

Обязательно с помощью производный калькулятор упростит работу с довольно сложными функциями. Процесс дифференциации упрощается за счет использования общих, легко запоминающихся Правила производных , включая Правило Продукта , правило квоты а также Правило цепи .

Эти правила помогут вам иметь дело с каждой дифференцируемой функцией, но алгебраический процесс вычисления и упрощение может быть не обязательно легким.