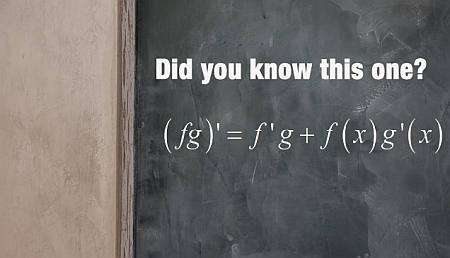Подробнее о правиле о товаре
Этот калькулятор поможет вам найти производную функции, используя правило произведения. Для того чтобы воспользоваться калькулятором, вам необходимо указать действительную функцию, для которой существует произведение.
Примером правильной функции может быть что-то вроде f(x) = x*sin(x), или что-то вроде g(x) = sin(x)*cos(x), и это лишь некоторые примеры.
Затем набираем функцию, для которой вы хотите использовать правило произведения, после чего нужно нажать кнопку "Рассчитать", и все шаги вычислений будут вам предоставлены.
Одним из первых правил производной, которое вы изучите, действительно является правило произведения, поскольку большинство функций, которые вы строите из элементарных функций, используют произведение функций.

Формула правила продукта
Изучение
производное правило
это, возможно, первое, что вы сделаете, когда будете учиться тому, как
найти производную
функции. И одно из первых правил, которое вы изучите, - это правило произведения, без сомнения.
Правило произведения, проще говоря, это правило, которое помогает вычислить производную от произведения функций. Формула правила произведения имеет вид:
\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]
Шаги по использованию правила продукта
-
Шаг 1:
Четко определите функции f(x) и g(x), которые образуют продукт, с которым вы работаете
-
Шаг 2:
При необходимости упростить, сохраняя структуру продукта
-
Шаг 3:
Используйте формулу правила произведения: \((f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \), которая предполагает подстановку значений функций f(x) и g(x), а также их производных f'(x) и g'(x)
Работая с производной по правилу произведения, вы, по сути, получаете производную от произведения, основываясь на знании отдельных функций и их производных.
Какие еще существуют правила работы с деривативами?
Помимо правила произведения, существуют и другие важные правила, такие как правило линейности, правило
Правило квоты
в котором говорится, что \(\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\), и
Правило цепи
в котором говорится, что \(\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)\).
Вы также найдете другие правила, упоминаемые повсюду, такие как правило мощности, которое указывает, что \(\frac{d}{dx} x^n = n x^{n-1}\), для постоянной \(n\).

Советы и рекомендации
Правило произведения можно рассматривать как правило умножения производных, и правило произведения играет важную роль в Calculus, поэтому его полезно хорошо выучить.
Обратите внимание, что в случае многозначных функций можно использовать правило умножения матриц, чтобы работать с правилом произведения.
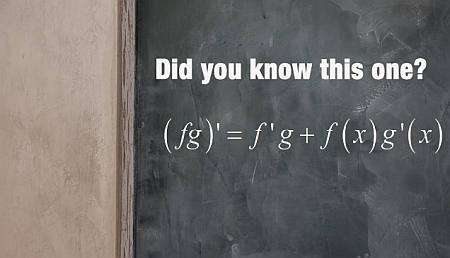
Пример: использование правила продукта
Вычислите производную от: \(f(x) = (x-1)(2x+1) \)
Отвечать:
Мы рассматриваем следующую функцию \(\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)\), которую необходимо дифференцировать.
\( \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)\)
By using the Product Rule: \(\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
By linearity, we know \(\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\) and \(\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)\)
Since the derivative of a constant is 0, we find that:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)\)
It is known that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)\)
So, we directly get: \(\frac{d}{dx}\left( 2x \right) = 2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2\left(x-1\right)\)
Note that \((2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2x-2\)
Grouping the terms with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+1-2\)
Grouping together numerical values and operating the terms that were grouped with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x+1-2\)
Reducing the integers that can be subtracted together: \(\displaystyle 1-2 = -1\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x-1\)
Вывод
: Следовательно, можно сделать вывод, что производная функции равна:
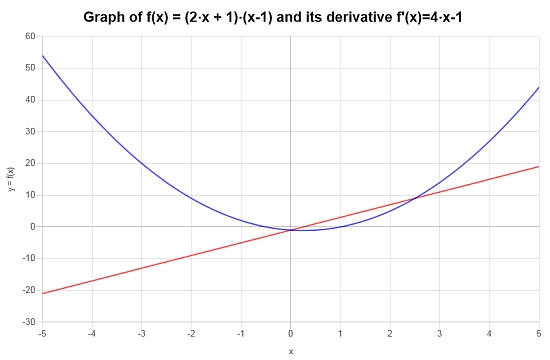
\[f'(x) = 4x-1\]
Графически ситуация представлена следующим графиком:
Примеры правил для продуктов
Найдите производную от: \(f(x) = x \sin(x)\)
Отвечать:
В данном примере заданной функцией является \(\displaystyle f(x)=x\sin\left(x\right)\). Найдем ее производную
\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)
Мы используем правило продукта: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
Путем прямого дифференцирования находим: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)
Таким образом, после упрощения мы получаем следующее:
\( \displaystyle = \,\,\)
\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)
Вывод
: Отсюда следует, что производная дается следующей формулой:
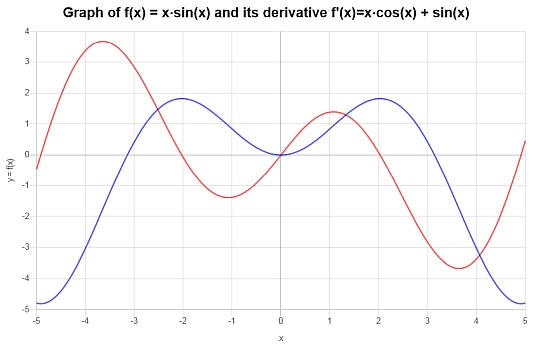
\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]
Для функции и ее производной построен следующий график:
Пример: расчет правила другого продукта
Продифференцируйте следующую функцию \( f(x) = x (x+1)^2 \).
Отвечать:
Наконец, для данного примера заданной функцией является \(\displaystyle f(x)=x\left(x+1\right)^2\). Поскольку существует произведение функций, мы можем использовать правило произведения для дифференцирования.
\( \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)\)
Мы используем правило продукта: \(\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
Мы знаем, что \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \)
Использование правила мощности для постоянной экспоненты: \(\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 \)
По линейности мы знаем \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), поэтому подключаем это:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 \)
Производная от константы равна 0, тогда:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 \)
Мы знаем, что \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 \)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)^2+2\left(x+1\right)x\)
Расширение терминов: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x\)
Обратите внимание, что \((x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1\), так как мы можем использовать распределительное свойство для каждого члена выражения слева, по отношению к членам справа
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x+1\right)x\)
Обратите внимание, что \((x+1) \cdot (x) = x^2+1x = x^2+x\), благодаря тому, что мы можем использовать распределительное свойство на каждом члене выражения слева, по отношению к членам справа
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x^2+x\right)\)
Мы получаем \((2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x\), используя распределительное свойство для каждого члена выражения слева по отношению к членам справа
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2x^2+2x\)
Группировка терминов с помощью \(x\), \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1\)
Сложение целых чисел и упрощение терминов, которые были сгруппированы с \(x\), \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x+3x^2+1\)
Таким образом, мы получаем
\( \displaystyle = \,\,\)
\(\displaystyle \left(3x+1\right)\left(x+1\right)\)
Вывод
: Исходя из того, что было вычислено выше, выясняется, что соответствующая производная имеет вид:
\[f'(x) = \left(3x+1\right)\left(x+1\right)\]
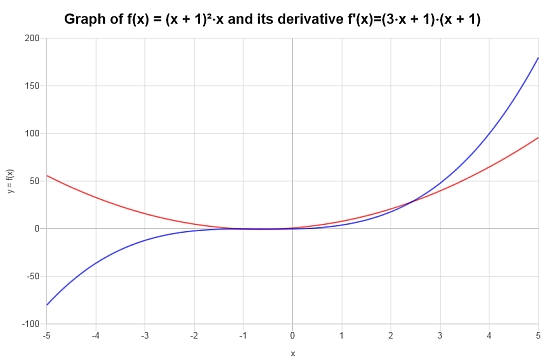
Для заданной функции на интервале \([-5, 5]\) получен следующий график:
Другие производные калькуляторы
Мало кто не согласится с тем, что дифференцирование, наряду с интегрированием, является центральным пунктом Calculus.
Вычисление производной
это важнейший навык, который вам необходимо освоить, изучая математику.
Вы можете изучить различные "вкусы" дифференциации, включая
частичная дифференциация
так же как
неявное дифференцирование
которые используются в различных контекстах применения.
Приложения включают
Касательная линия
расчет, который является таким же, как
Линейное Приближение
, а также использование производных более высокого порядка, начиная с
производные второго порядка
.