Неявное дифференцирование

Данный калькулятор поможет вам провести неявное дифференцирование для уравнения, в котором участвуют переменные x и y. Вам необходимо предоставить действительное уравнение, например, x^2 + y^2 = 1, или xy - x^2 y^2 = 0 и т.д.

Как только вы предоставите действительное уравнение с двумя переменными (\(x\) и \(y\)), все, что вам нужно сделать, это нажать кнопку "Вычислить", и будут показаны все шаги соответствующего неявного дифференцирования.

Это Калькулятор dy/dx с шагами в том смысле, что он покажет вам все соответствующие этапы расчета производной одной переменной по другой, если эти две переменные связаны в одном уравнении. Именно эта связь позволяет найти соответствующее неявная производная .

Имея уравнение, связывающее две переменные \(x\) и \(y\), мы можем выразить \(y\) как функцию \(x\) и записать \(y = y(x)\). Часто мы не можем явно выразить \(y\) как функцию \(x\). Мы предполагаем, что такая функция существует, и в этом случае имеет смысл дифференцировать \(y\) относительно \(x\).

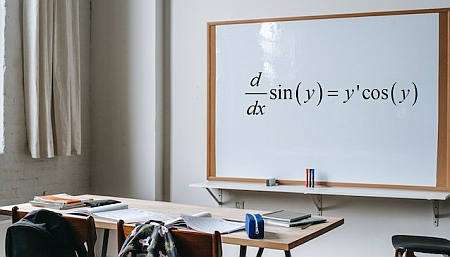
Что такое неявная дифференциация?

Неявное дифференцирование – это расчет дифференциации Метод основан на предположении, что из данного уравнения, включающего \(x\) и \(y\), можно утверждать, что \(y\) является функцией \(x\), хотя часто мы не можем написать такую функцию явно.

Сделав это предположение, мы предполагаем, что можем вычислить \(\frac{dy}{dx}\) и можем использовать все известные Правила производных ( Правило Продукта , Правило квоты и Правило цепи ), чтобы дифференцировать обе части уравнения и найти \(\frac{dy}{dx}\).

В чем заключается метод неявного дифференцирования?

Метод неявного дифференцирования — это метод, который позволяет вычислить производную для выражений, которые не представлены непосредственно в формате \(f(x)\). Например, когда нам дана функция переменной \(x\), мы просто идем дальше и дифференцируем эту функцию.

Но когда две переменные \(x\) и \(y\) связаны уравнением, например \(x^2+y^2 = 1\), вы также можете дифференцировать y по x, в соответствии с традиционным методом вам нужно будет РЕШИТЬ y через x, и ТОГДА вы сможете различать.

Используя неявное дифференцирование, вы можете дифференцировать напрямую, просто предположив, что \(y = y(x\), и используя Правило цепи .

Шаги для использования неявного дифференцирования

• Шаг 1: Определите уравнение, в котором участвуют две переменные x и y. Упростите все лишние члены
• Шаг 2: Предположим, что y является функцией от x, y = y(x), поэтому имеет смысл вычислить производную y по отношению к x
• Шаг 3: Вычислите производную обеих сторон уравнения, используя все Правила производных что вам нужно. Это приведет к равенству, в котором x, y и y' присутствуют потенциально
• Шаг 4: Решите для y' то, что вы получили в шаге 3. Обратите внимание, что y' обычно записывается как функция от x и y, что вполне нормально, поскольку y также зависит от x

Это очень общая методология, и она будет иметь тонкости от случая к случаю, но это план, который должен работать в большинстве случаев, с дополнительными потенциальными трудностями алгебраических манипуляций.

Зачем использовать калькулятор неявного дифференцирования

Неявное дифференцирование иногда может сбить с толку, если вы не очень четко представляете, что вы дифференцируете и относительно какой переменной. Калькулятор поможет вам сравнить результат, а особенность нашего калькулятора в том, что все этапы процесса показаны.

Это очень важная помощь для вас, потому что она покажет вам, какое именно производное правило и где вы его применили.

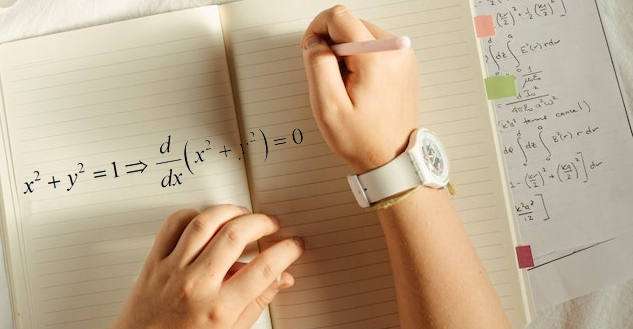
В чем смысл неявной дифференциации?

Это справедливый вопрос. Если у вас есть уравнение, включающее x и y, почему бы не решить y в терминах x и не использовать обычное вычисление производной для получения производной y относительно x. Я могу назвать вам по крайней мере две веские причины:

• Причина 1: Может случиться так, что вы не сможете решить y в явном виде в терминах x. Функция может существовать, но вы не можете просто найти ее. Вспомните y + tan(y) = x^2
• Причина 2: Даже если вы случайно решить y в терминах x но это может быть действительно сложное выражение, и вычисление производной может быть очень запутанным и трудным. Обычно неявное дифференцирование алгебраически просто, в относительных терминах

Зависит ли неявная производная от y?

Не всегда, но часто. Это всего лишь утверждение, что \(\frac{dy}{dx}\) может зависеть от x и y, но поскольку y зависит от x, это просто означает, что, как и ожидалось, \(\frac{dy}{dx}\) зависит от x.

В следующем разделе будут представлены различные примеры неявного дифференцирования.

Вторая неявная производная

Один вопрос: можно ли вычислить вторую производную, используя неявное дифференцирование? Ответ: ДА. Вы просто делаете то же самое, что и с первой производной, используя неявное дифференцирование: вы просто предполагаете, что \(y\) является функцией \(x\), поэтому вы пишете \(y = y(x)\) и можете дифференцировать столько, сколько пожелаете.

Например, предположим, что вы хотите найти \(\frac{d^2y}{dx^2}\) по уравнению \(x^2+y^2=1\). Дифференцирование обеих сторон по \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Теперь вы снова дифференцируете по x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

и теперь решаем \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Пример: пример неявного дифференцирования

Найдите \(\frac{dy}{dx}\) для уравнения: \(x^2 - y^2 = 2y\)

Отвечать: Это пример неявной дифференциации. Было предоставлено следующее уравнение: \(\displaystyle x^2-y^2=2y\), для которого нам нужно провести неявное дифференцирование, где мы предполагаем, что \(y\) является функцией \(x\) .

Уравнение не требует дальнейшего упрощения, поэтому мы можем перейти к неявному дифференцированию:

Нам нужно продифференцировать обе части уравнения по \(x\), и в обеих частях мы предполагаем, что \(y = y(x)\).

Левая сторона : Дифференцирование левой части по \(x\).

Правая сторона : Дифференцирование правой части по \(x\).

Следовательно, после дифференцирования обеих частей по \(x\) получается следующее:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Размещение всех терминов на одной стороне:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Группируем все, что содержит \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Наконец, решение \(\displaystyle \frac{dy}{dx}\) приводит к:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Пример: больше неявных вычислений дифференцирования

Каков наклон касательной к единичной окружности в точке \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)?

Отвечать: Обратите внимание, что уравнение единичной окружности — \(\displaystyle x^2 + y^2 = 1\), что неявно определяет \(y\) как функцию \(x\). Чтобы найти касательную, нам нужно вычислить \(\frac{dy}{dx}\) в указанной точке. Используя неявное дифференцирование, мы дифференцируем обе части уравнения, определяющего единичный круг: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

Интерес представляет \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), так что .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Это означает, что наклон касательной в точке \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) равен \(m = -1\), а это означает, что уравнение касательной в этой точке имеет вид

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Пример неявного дифференцирования

Рассмотрим уравнение: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Вычислить \(\frac{dy}{dx}\)

Отвечать: В данном случае у нас есть следующее уравнение: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), поэтому нам нужно выполнить неявное дифференцирование в предположении, что \(y\) зависит от\(x\) .

Дальнейшее упрощение уравнения не требуется, что позволяет перейти к неявному дифференцированию:

Теперь нам нужно вычислить производную обеих частей по переменной \(x\), считая, что \(y = y(x)\).

Левая сторона : Дифференцирование левой части по переменной \(x\)

Правая сторона : Теперь дифференцируем правую часть по \(x\).

Следовательно, результат, который получается после дифференцирования обеих частей по \(x\), следующий:

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Следовательно, теперь мы можем найти \(\displaystyle \frac{dy}{dx}\), чтобы получить:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

Другие полезные решатели задач calculus

Одно из самых интересных применений правила обращения с производными финансовыми инструментами является концепция неявного дифференцирования. Она находит применение в физике, экономике и инженерном деле, а также имеет огромное практическое значение для описания скорости изменения вдоль кривых.

Другим типом производных инструментов являются частные производные в котором, в отличие от случая неявного дифференцирования, когда мы предполагаем, что y = y(x), в этом случае y считается константой при изменении x.