Решатели Calculus

Правила производных

Инструкции: Используйте этот калькулятор производных для нахождения производной любой заданной вами функции, используя наиболее распространенные правила вычисления производных и показывая все шаги. Пожалуйста, введите функцию, к которой вы хотите применить правила вычисления производной, в поле формы ниже.

О правилах производных

Этот калькулятор позволит вам вычислить производную заданной функции, применяя необходимые основные правила дифференцирования, показывая все этапы процесса и отмечая, где применяется каждое правило.

Вам просто нужно предоставить действительную функцию, которая является дифференцируемой (что означает, что у нее есть производная). Например, допустимой функцией может быть f(x) = 1/3*x*sin(x), просто чтобы упомянуть один пример.

Затем, когда вы уже набрали свою функцию, просто нажмите "Calculate", чтобы получить все шаги дифференцирования, показанные на экране.

Простота правил производных делает процесс дифференциации таким, который признается "легким", что, возможно, является преувеличением.

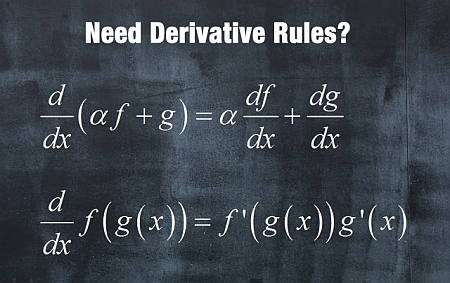
Основные правила работы с деривативами

Вы должны усвоить четыре основных правила работы с деривативами

Правило Линейности: Для функций \(f(x)\) и \(g(x)\), и константы \(a\), производная является линейной операцией: \((af(x)+g(x))' = af'(x)+g'(x)\)
Правило Продукта Для функций \(f(x)\) и \(g(x)\) производная произведения равна \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
Правило Квоты: Для функций \(f(x)\) и \(g(x)\) производная от коэффициента равна \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
Правило Цепи Для функций \(f(x)\) и \(g(x)\) производная составной функции равна \((f(g(x)))' = f'(g(x))g'(x)\)

Это правило будет работать как шарм и поможет вам найти производную любой базовой функции.

Как использовать правила производных?

Шаг 1: Определите функцию f(x), которую вы хотите дифференцировать, упростите при необходимости
Шаг 2: Попытайтесь разбить функцию на более мелкие производные, используя линейность
Шаг 3: В зависимости от структуры функции f(x), используйте любое из доступных правил (произведение, коэффициент и правило цепочки), и имейте в виду, что вам может понадобиться применить многие из правил последовательно)

Обычно в итоге вы используете комбинацию из нескольких правил дифференцирования, пока не дойдете до точки, где найдете элементарную функцию, которую вы уже знаете, как дифференцировать.

Могу ли я решить все производные

Сказать, что использование правил дифференцирования может привести вас к решению ВСЕХ производных, будет преувеличением. Вы сможете решить большинство производных, и, конечно, все основные производные, но есть функции с менее интуитивным поведением, которые можно определить, хотя они обычно не рассматриваются в базовых курсах Calculus.

Что касается основных функций, то большинство из них дифференцируются без проблем.

A правило продукта , правило котировки производной или же производная по цепному правилу вряд ли будут изолированы друг от друга, скорее всего, они будут представлены в виде последовательности из нескольких правил, которые необходимо использовать вместе.

Пример: правила производных

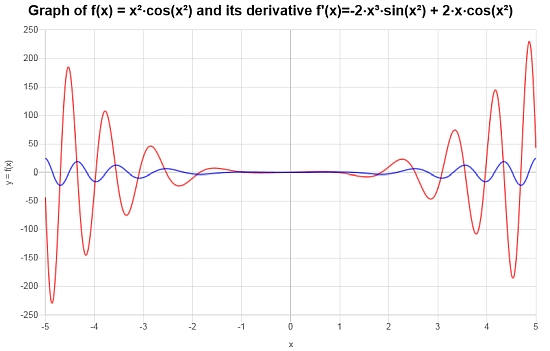
Используя основные правила вычисления производной, вычислите следующую производную: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)

Отвечать: Рассмотрим следующую заданную функцию, для которой необходимо вычислить производную \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)

Функция не нуждается в упрощении, поэтому мы можем сразу перейти к вычислению ее производной:

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

Соответствующий график функции и ее производной показан ниже:

Пример: больше правил производных

Вычислите следующую производную: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\), используя основные правила вычисления производной.

Отвечать: Теперь задача заключается в дифференцировании функции \(\displaystyle f(x)=x\cos\left(x^2+1\right)\)

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

Пример правил производных

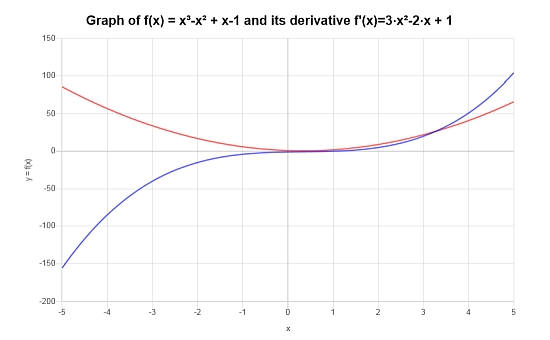
Для функции \( f(x) = (x-1)(x^2+1) \), используя правила производной, найдите ее производную.

Отвечать: Для этого последнего примера нам нужно провести дифференциацию: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\).

Начальный Этап: В этом случае нам сначала нужно расширить заданную функцию \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \), и для этого мы проводим следующие шаги упрощения:

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

После расширения функции мы можем перейти к вычислению производной:

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2-2x+1\)

Графически функция и ее производная выглядят так:

Другие производные калькуляторы

Одна из магий дифференциации заключается в том, что вы можете найти производную любой функции, используя некоторые основные и простые правила, включая Правило Продукта , Правило квоты и естественно, правило цепи . Этого небольшого арсенала обычно достаточно для вычисления любой производной, которая вам нужна

Дифференцирование и интегрирование - это основные дорожки в Calculus, без всякого спора, поскольку они являются центром стольких приложений, во всех аспектах науки. От связанных ставок до неявное дифференцирование , с частные производные в физике и экономике