Калькулятор линейной аппроксимации

Этот калькулятор линеаризации позволит вычислить линейное приближение, также известное как Касательная линия для любой данной действительной функции в данной действительной точке.

Вам необходимо указать допустимую функцию, например, f(x) = x*sin(x) или f(x) = x^2 - 2x + 1, или любую допустимую функцию, которая является дифференцируемой, и точку \(x_0\) где функция корректно определена. Эта точка может быть любым допустимым числовым выражением, например, 1/3.

Как только вы укажете действительную функцию и точку, вы нажмете "Рассчитать", и все расчеты будут показаны для вас.

Линейное приближение или приближение первого порядка ищет приближение данной функции линией в заданной точке \(x_0\). Естественно, для кривых линейная аппроксимация будет грубой, хотя основная идея заключается в том, что аппроксимация будет точной для точек, близких к \(x_0\).

Линейное приближение

Идея состоит в том, чтобы найти прямую, проходящую через точку \((x_0, f(x_0))\) и "едва касающуюся" функции \(f(x)\). Формальное математическое определение "едва касаясь" дается идеей Касательная линия для чего нам необходимо вычислить производную функции.

На самом деле формула для линейной аппроксимации в точке \(x_0\) зависит от производной \(f'(x_0)\) следующим образом

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Этот формула линейной аппроксимации по существу определяет уравнение линии которая проходит через точку \((x_0, f(x_0))\), поэтому и называется "линейной аппроксимацией", так как определяет линейную функцию, совпадающую с \(f(x)\) в точке \(x_0\) и очень близкую к \(f(x)\) для значений \(x\), близкие к \(x_0\).

Шаги для нахождения линейной аппроксимации

• Шаг 1: У вас должна быть заданная функция f(x) и точка x0. Функция должна быть дифференцируемой в точке x0
• Шаг 2: Вычислите f(x0) и f'(x0), которые являются функцией и производной функции f в точке x0
• Шаг 3: Определим линейное приближение как y = f(x_0) + f'(x_0) (x - x_0), которое представляет собой формулу линеаризации, представленную выше.

Эта линия \(y = f(x_0) + f'(x_0) (x - x_0)\) представляет приближение первого порядка, также известное как локальное линейное приближение.

Связь с касательной линией

Как вы уже, наверное, догадались, линейное приближение - это то же самое, что и Касательная линия в данной точке. Тогда вычисление линейной аппроксимации точно такое же, как и вычисление касательной линии

Другое название того же - приближение первого порядка или приближение касательной линии, которые также часто используются в исчислении.

Дифференциальная и линейная аппроксимация

Другое распространенное понятие — понятие дифференциала, которое тесно связано с понятием линейного приближения и является просто его производным. Действительно, дифференциал (или конечная разность) определяется как \(\Delta y = y - f(x_0)\). Тогда, основываясь на формуле первого приближения, формула для дифференциала имеет вид

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Естественно, это выглядит точно так же, как формула линейной аппроксимации, за исключением того, что член \(f(x_0\) передается слева.

Пример: вычисление аппроксимации первого порядка.

Рассмотрим следующее: \(f(x) = x^2 - 2x + 3\), найти его приближение первого порядка в \(x_0 = 1\).

Отвечать: Предоставленная функция — \(\displaystyle f(x)=x^2-2x+3\), и нам нужно найти линейное приближение вокруг точки x = 1. Итак, сначала нам нужна производная.

Линейное Приближение : Уравнение для линейного приближения, которое мы ищем в точке \(x_0 = 2\), задается следующей формулой

\[y = y_0 + f'(x_0)(x - x_0) \]

Обратите внимание, что по определению \(\displaystyle y_0 = f(x_0)\), которое подразумевает, что нам нужно подключить функцию в точке \(x_0 = 2\):

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Делаем то же самое, но теперь для производной в точке \(x_0 = 2\), так что тогда

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Теперь с этим мы возвращаемся к формуле линейной аппроксимации:

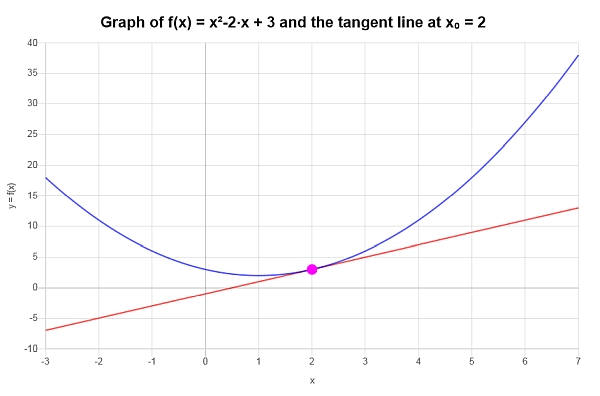
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Заключение : Мы заключаем, что линейная аппроксимация для \(\displaystyle f(x)=x^2-2x+3\) в точке \(x_0 = 2\) определяется следующим образом:

\[y = 2x-1 \]

Графически:

Пример: больше аппроксимации первого порядка

Для функции : \(f(x) = x \sin(x)\) и точки \(x_0 = 2\) найдите соответствующее приближение первого порядка.

Отвечать: В этом случае функция, которая нам нужна для работы: \(\displaystyle f(x)=x\sin\left(x\right)\).

Теперь вычислим его производную:

Линейное Приближение : Уравнение линейной аппроксимации имеет вид:

\[y = y_0 + f'(x_0)(x - x_0) \]

где \(\displaystyle y_0 = f(x_0)\), то мы вычисляем:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Для производной в \(x_0 = 2\) мы находим, что:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Теперь мы готовы подставить их обратно в формулу аппроксимации первого порядка:

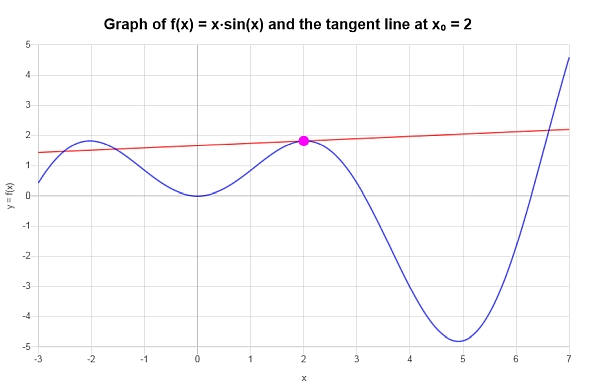
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Заключение : Делается вывод, что линейная аппроксимация \(\displaystyle f(x)=x\sin\left(x\right)\) в заданной точке \(x_0 = 2\) вычисляется как:

\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Графически мы получаем следующий график:

Пример: расчет линейного приближения

Вычислите приближение первого порядка для \( f(x) = \frac{\sin(x)}{x}\) в \(x = \frac{\pi}{4}\).

Отвечать: Предусмотрена следующая функция: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), для которой нам нужно вычислить ее производную.

Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:

Аппроксимация Первого Порядка : Уравнение для соответствующего приближения первого порядка для заданной функции \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) в заданной точке \(x_0 = \frac{\pi}{4}\) задается следующим образом:

\[y = y_0 + f'(x_0)(x - x_0) \]

Подставляем соответствующие значения:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Теперь мы можем подставить это в формулу:

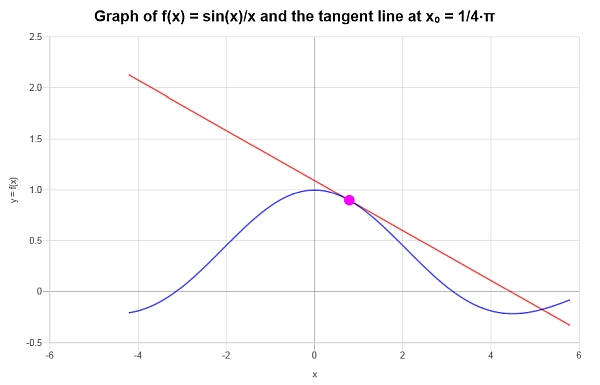
\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Заключение : Таким образом, мы можем заключить, что приближение первого порядка для данной функции \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) в данной точке \(x_0 = \frac{\pi}{4}\) определяется выражением

\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Графически получается следующее:

Другие калькуляторы производных инструментов

Помимо этого калькулятор линеаризации , вы можете найти много вещей, которые делают разные вещи на основе производных. Дифференциация является важной операцией в исчислении, физике, технике и экономике с широким спектром приложений.

Существует также способ провести линейную аппроксимацию для большего количества переменных, например, для функции \f(x, y)\), и в этом случае формула линейной аппроксимации становится \(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\), поэтому в этом случае чтобы найти линеаризацию, нам нужно использовать частные производные .

Нахождение линеаризации функции далеко не единственное, что вы можете делать с производными. Дифференциация — относительно простая операция с простыми правилами, такими как Правило Продукта , правило квоты и Правило цепи что делает расчет производных относительно простой операцией.

Хотя предполагается, что она должна быть простой, рекомендуется использовать производный калькулятор чтобы получить все показанные шаги, с четким упоминанием всех Правила производных используется.