Подробнее о линейные уравнения

Этот калькулятор поможет вам построить график линейного уравнения, которое вы предоставите. Итак, первым шагом является предоставление действительного линейного уравнения, например 2x + 3y = 4, или вы можете предоставить что-то, что не упрощается напрямую, например 2/3 x + y = 4/3 x - 1/2 y + 2. Подойдет любое действительное линейное выражение. .

После того, как вы предоставите действительное линейное уравнение, наступает самое легкое время, поскольку все, что вам нужно сделать, это нажать кнопку "Вычислить", и вам будут показаны этапы процесса построения графика линейной функции.

Линейные уравнения будут играть важную роль во многих операциях, в том числе для решить систему линейных уравнений .

Формула линейного уравнения

Существуют различные формы, в которых можно записать формулу линейного уравнения. Наиболее распространенными являются стандартная форма , который показан ниже

\[a x + by = c \]

Кроме того, существует форма пересечения наклона , который показан ниже

\[y = mx + n\]

Эти две формы могут быть преобразованы из одной в другую, за исключением пары исключений, а именно вертикальной линии, выраженной x = a. Эта линия вертикальна и пересекает ось x в точке (a, 0). Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной)

Каковы этапы построения графика линейного уравнения?

• Шаг 1: Четко определите имеющееся уравнение
• Шаг 2: Посмотрите коэффициент, который умножает y, если он равен нулю, то у вас есть вертикальная линия
• Шаг 3: Если коэффициент, умножающий y, отличен от нуля, то вы решаете для y, чтобы получить форма пересечения наклона
• Шаг 4: Используя форму "наклон-пересечение", оцените функцию при x = 0 и x = 1, и тогда у вас будет две точки, через которые проходит прямая
• Шаг 5: Проведите линию, используя две найденные точки в качестве ориентира

Один из самых четких способов провести линию - это иметь две точки, через которые проходит линия, так как часто использование наклона для ориентира может ввести в заблуждение.

Решение линейного уравнения в одной переменной

Студенты знакомы с системами линейных уравнений, и они более или менее понимают, что нужно сделать. Но затем они задаются вопросом о решении линейного уравнения с одной переменной. Допустим, у вас есть линейное уравнение в форме "наклон-пересечение":

\[y = a + bx \]

Как же решить эту проблему? Ну, она уже решена: Для каждого заданного значения x решение y равно y = a + bx. Таким образом, при условии, что \(b \ne 0\), у вас есть бесконечное множество решений линейного уравнения.

Ситуация меняется, когда у вас есть два линейных уравнения, в этом случае вам нужно решить оба уравнения одновременно .

Так ли важны линейные уравнения?

Еще бы! Пожалуй, один из самых важных во всей математике. Это объясняется простотой и в то же время широким спектром применения.

Пример: калькулятор линейных уравнений

Получите график следующего линейного уравнения: \(\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0\)

Решение:

Получите уравнение линии в форме наклон-пересечение

Нам было дано следующее уравнение..:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Упрощение констант:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Теперь, положив \(y\) в левой части, \(x\) и константу в правой части, получим

\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{7}{4}\), получается следующее

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]

и упрощая окончательно получаем следующее

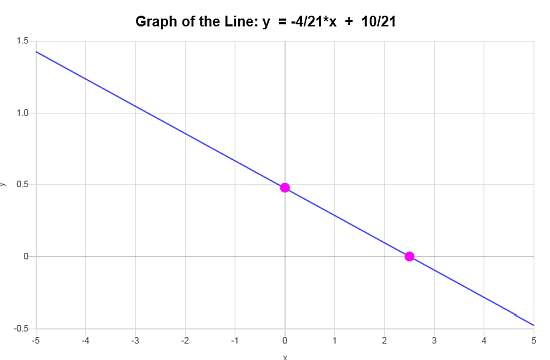
\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]

Вывод : На основании имеющихся данных мы делаем вывод, что уравнение линии в форме наклонная-пересечение имеет вид: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), с наклоном \(\displaystyle b = -\frac{4}{21}\) и y-перехватом \(\displaystyle n = \frac{10}{21}\).

Учитывая эти данные, представленный линейный график показывает

Пример: пример калькулятора линейных уравнений

Вычислите следующее: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)

Отвечать: Теперь мы получили следующее уравнение:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Первый шаг - упрощение констант:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Поместив \(y\) в левую часть, а \(x\) и постоянный член в правую часть, получим

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]

Теперь нам нужно решить \(y\), что достигается делением обеих сторон уравнения на \(\frac{5}{4}\), и получается следующее

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]

и упрощая окончательно получаем следующее

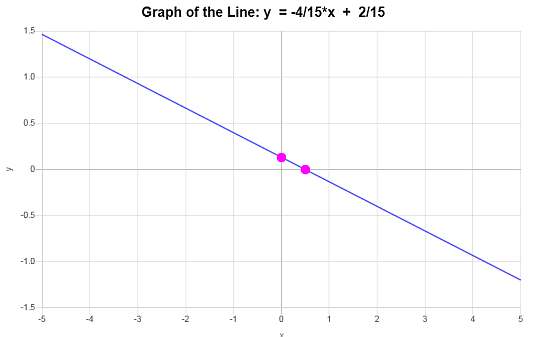
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]

Вывод : Уравнение линии в форме наклон-пересечение, согласно представленной информации, равно \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), с наклоном \(\displaystyle b = -\frac{4}{15}\) и y-пересечением \(\displaystyle n = \frac{2}{15}\).

Согласно этим данным, представленный линейный график имеет вид

Пример: еще один пример калькулятора линейных уравнений

Представляет ли это линию: \( y = 5 \). Если да, то каковы ее характеристики?

Отвечать: Да, это так. Действительно, когда у вас есть выражение типа \( y = 5 \), у вас есть линейное уравнение в форме "наклон-пересечение", с a = 0 и b = 5. Следовательно, мы имеем горизонтальную линию, которая пересекает ось y в точке (0, 5).

Больше калькуляторов по алгебре

Линии , Линейные уравнения и линейные функции всегда будет играть решающую роль в алгебре, представляя также четкую связь с некоторыми основными геометрическими свойствами.

С точки зрения применения, возможно Решение систем линейных уравнений является одним из самых распространенных применений линий и линейных уравнений.