Per saperne di più su questo creatore di P-Chart.

Questo calcolatore P-chart è uno strumento grafico molto usato per valutare se un processo è in controllo statistico, di solito analizzando il comportamento della proporzione di difetto su molti campioni.

Il grande vantaggio di usare uno strumento grafico è che si possono facilmente trovare modelli e identificare punti che sembrano deviare da un comportamento "normale", o più precisamente, ciò che ci si aspetterebbe sotto certe comuni ipotesi distributive.

Come si usa questa calcolatrice di carte P online?

L'idea è che avete una lista di campioni \(N\), e per ogni campione avete un numero di difetti e la dimensione del campione. Di solito la dimensione del campione è la stessa per tutti i campioni, ma non è sempre il caso.

Poi, per ogni campione si calcolerà la proporzione campionaria di difettosi \(\p_i\). Complessivamente, avremo \(N\) proporzione campionaria di difettosi, una per ogni campione. Infine, si trova la media della proporzione di difettosi, che si chiama \(\bar{p}\).

Dopo aver ottenuto tutto ciò, potete usare le seguenti formule per ottenere i limiti di controllo inferiori e superiori per il p-chart

\[ LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \] \[ UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \]

dove \(k\) è la dimensione del campione comune di TUTTI i campioni con cui state lavorando.

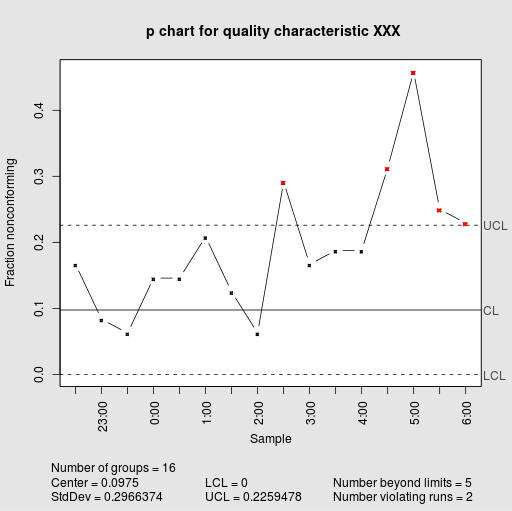
Riassumendo: come si fa un diagramma a P?

Passo 1. La prima cosa da fare è raccogliere i dati che si vogliono misurare, in questo caso, i difettosi, perché si è interessati ad analizzare la proporzione di difettosi alla fine.

Passo 2. Ora, per ogni campione si calcola la proporzione del campione di difettosi (che è il numero di difettosi diviso per la dimensione del campione).

Passo 3. Il passo successivo è quello di calcolare la media di tutte le proporzioni di difettosità del campione.

Passo 4. Poi è necessario utilizzare le formule per i limiti di controllo inferiori e superiori \(LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}}\) e \(UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \).

Passo 5. Ora si costruisce un grafico in cui si traccia la proporzione di difetti per ogni campione, sotto forma di un grafico a linee, e si devono anche tracciare i limiti inferiore e superiore, così come la linea centrale.

Passo 6. Nell'ultimo passo, si determina se una percentuale di difetti supera o meno uno dei limiti di controllo.

Quei punti che vanno oltre i limiti di controllo inferiore e superiore, se esistono, si dice che sono fuori controllo statistico, e anche il processo non è in controllo statistico. Quando nessun punto è fuori controllo statistico, allora diciamo che il processo è in controllo statistico.

Altra tabella di controllo

Potreste essere interessati a usare un Grafico R per valutare se la variabilità del processo è sotto controllo o meno. Inoltre, se avete bisogno di valutare se il centro del processo è in controllo statistico, potete usare questo Creatore di grafici X-bar .