समाधानकर्ताओं बीजगणित

बहुपद -ग्राफ

सराय: बहुपद कार्यों को रेखांकन के लिए इस कैलकुलेटर का उपयोग करें, नीचे दिए गए फॉर्म में आपके द्वारा प्रदान किए गए किसी भी बहुपद फ़ंक्शन का ग्राफ बनाने के लिए:

बहुपद -ग्राफ

इस कैलकुलेटर का उपयोग करें यदि आपको एक बहुपद फ़ंक्शन को रेखांकन करने में सहायता की आवश्यकता है।प्रक्रिया आसान है: आपको बस उस बहुपद कार्य को टाइप करना होगा जिसे आप ग्राफ करना चाहते हैं।आप '3x^3 + x - 1' जैसी कुछ लिख सकते हैं, या आप इसे फ़ंक्शन नाम के साथ प्रस्तावित कर सकते हैं, जैसे 'P (x) = 3x^3 + x - 1'।

प्रदान किए गए बहुपद के गुणांक को आवश्यक रूप से पूर्णांक होने की आवश्यकता नहीं है, वे अंश या किसी भी वैध बीजीय अभिव्यक्ति हो सकते हैं।आपके द्वारा प्रदान किया गया बहुपद सरल हो सकता है या नहीं, इससे कोई फर्क नहीं पड़ता।

फिर, एक बार बहुपद प्रदान किए जाने के बाद, आप वैकल्पिक रूप से एक्स मानों की सीमाओं को निर्धारित कर सकते हैं जो रेखांकन किया जाएगा, और फिर आप "गणना" पर क्लिक करते हैं, और शीघ्र ही, प्रक्रिया के सभी चरणों को दिखाया जाएगा।

तंग सबसे महत्वपूर्ण वस्तुओं में से एक हैं जो आपको बीजगणित के साथ -साथ कैलकुलस में भी मिलेंगे।इसके अलावा, बहुपद बहुपत्नी समीकरणों को हल करने की आवश्यकता को जन्म देता है, जिसमें जीवन के हर पहलू में, यहां तक कि गणित से परे, हर जगह बहुत सारे अनुप्रयोग होते हैं।

बहुपद कार्यों की मूल बातें

आइए हम याद करते हैं कि एक बहुपद समारोह में निम्नलिखित रूप है:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

जहां हम मानते हैं कि \(a_n \ne 0\), और हम कहते हैं कि बहुपद की t डिगthirी इस मामले में \(n\) के बराबर है, और प्रमुख गुणांक \(a_n\) है।एक बहुपद की डिग्री को परिभाषित करने का आम आदमी यह है कि यह बहुपद अभिव्यक्ति में मौजूद उच्चतम शक्ति से मेल खाता है।

उदाहरण के लिए, \(p(x) = 3x^2 + 2x - 1\) डिग्री 2 का एक बहुपद है, और इसका प्रमुख गुणांक 3. है। अब, \(p(x) = \sin(3x^2 + 2x - 1)\) उदाहरण के लिए, बहुपद नहीं है।

बहुपद रेखांकन कैसे करें?

सिद्धांत रूप में बहुपद रेखांकन किसी भी अन्य फ़ंक्शन को रेखांकन के समान दिखाते हैं।यदि आप इसे हाथ से करना चाहते हैं, तो आप x और y के लिए कई मानों को सारणीबद्ध करेंगे, और आप एक वक्र का पता लगाएंगे कि कम या ज्यादा आप अपनी मेज पर मिलने वाले बिंदुओं से गुजरेंगे।

स्वाभाविक रूप से, यह विधि थोड़ी आदिम है, क्योंकि सामान्य तौर पर हम जरूरी नहीं कि एक फ़ंक्शन का पूरा ग्राफ नहीं जान सकते, केवल उन बिंदुओं का एक गुच्छा जानकर जिन्हें हम सारणीबद्ध कर रहे हैं।

सौभाग्य से, बहुपद के लिए कार्य थोड़ा आसान है, और वास्तव में हम इसके प्रमुख गुणांक और इसकी डिग्री को जानकर इसके ग्राफ के बारे में बहुत कुछ जान सकते हैं।

बहुपद कार्यों को रेखांकन के लिए कदम

एक बहुपद का ग्राफ अंततः प्रत्येक बहुपद के विशिष्ट गुणांक पर निर्भर करता है।लेकिन हम एक बहुपद के अंतिम व्यवहार और वास्तविक जड़ों के अस्तित्व के बारे में कुछ मजबूत बयान दे सकते हैं।

आइए हम याद करते हैं कि एक बहुपद का अंतिम व्यवहार बहुपद का व्यवहार है जब एक्स बहुत बड़ा और नकारात्मक होता है, और जब एक्स बहुत बड़ा और सकारात्मक होता है।

Letsunt 1: बहुपद समारोह की पहचान करें, और यदि आप कर सकते हैं तो सरल करें, क्योंकि यह ग्राफ अभिव्यक्तियों के लिए आसान है जो सरल हैं
Therur the: क्या आप बहुपद की जड़ों को जानते हैं?यदि वे वास्तविक जड़ें हैं, तो आप उन बिंदुओं को जानते हैं जहां बहुपद एक्स-एक्सिस को पार करता है, जो आपको एक मजबूत ग्राफिकल संदर्भ देता है
Theirण 3: यदि बहुपद की डिग्री विषम है, तो अंतिम व्यवहार बड़े नकारात्मक एक्स मानों और बड़े सकारात्मक एक्स मानों के लिए विपरीत होगा।यदि प्रमुख गुणांक सकारात्मक है, तो बड़े नकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और नकारात्मक होगा, और बड़े सकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और सकारात्मक होगा।यदि प्रमुख गुणांक नकारात्मक है, तो बड़े नकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और सकारात्मक होगा, और बड़े सकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और नकारात्मक होगा
Reyrur 4: यदि बहुपद की डिग्री भी है, तो अंतिम व्यवहार बड़े नकारात्मक एक्स मानों और बड़े सकारात्मक एक्स मानों के लिए समान होगा।यदि प्रमुख गुणांक सकारात्मक है, तो बड़े नकारात्मक और सकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और सकारात्मक होगा।यदि प्रमुख गुणांक नकारात्मक है, तो बड़े नकारात्मक और सकारात्मक x मूल्यों के लिए बहुपद बहुत बड़ा और नकारात्मक होगा
च ५: ५: यदि बहुपद की डिग्री विषम है, तो बहुपद कम से कम एक बार एक्स-एक्सिस (इसलिए इसमें कम से कम एक वास्तविक जड़ है) को पार कर जाएगा, जबकि एक समान डिग्री के लिए, बहुपद जरूरी नहीं कि एक्स-एक्सिस को पार करें
च viry: 6: डिग्री एन का एक बहुपद अधिकांश एन समय पर एक्स-एक्सिस को पार करेगा।उदाहरण के लिए, 4 डिग्री 4 का एक बहुपद 4 बार एक्स-एक्सिस को पार कर सकता है

तो उदाहरण के लिए, एक क्यूबिक बहुपद, अधिक से अधिक 3 बार एक्स-अक्ष को पार कर सकता है, लेकिन यह नहीं है।

ग्राफिंग कैलकुलेटर

रेखांकन कैलकुलेटर का उपयोग करने के क्या फायदे हैं?अनेक।यह कहना नहीं है कि यह एक अच्छा कौशल नहीं है जो पेन और पेपर का उपयोग करके एक बहुपद को सटीक रूप से स्केच करने में सक्षम है।

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

Vayas 1: आप सुनिश्चित करते हैं कि आपको बहुपद के वास्तविक ग्राफ का सटीक चित्रण मिले
Vabay 2: आप अपने काम की जांच करने के लिए इसका उपयोग कर सकते हैं, यह सुनिश्चित करने के लिए कि क्या आप सही चरणों का पालन कर रहे थे
Vabay 3: ग्राफ के सबसे प्रासंगिक पहलुओं को दिखाने के लिए एक उपयुक्त विंडो चुनें

एक अच्छा ग्राफ आपको एक फ़ंक्शन के गुणों के बारे में बहुत कुछ बता सकता है, और वही एक बहुपद के लिए जाता है।रेखांकन बहुपद आपको वास्तव में यह कल्पना करने में मदद कर सकता है कि बहुपद किस प्रकार की जड़ों की है।

युक्तियाँ और चालें

एक बहुपद ग्राफ में जो आप देखते हैं, उसमें अति-पढ़ने से सावधान रहें।आप आसानी से बहुलता के साथ जड़ों के बारे में ज्यादा नहीं बता सकते हैं, इसलिए कुछ भी वास्तविक कार्य को प्रतिस्थापित नहीं करता है।

यदि आप अन्य प्रकार के कार्यों की कोशिश करना चाहते हैं, तो यह प्रयास करें तमाम औजार।

उदाहरण: बहुपद कार्यों को रेखांकन

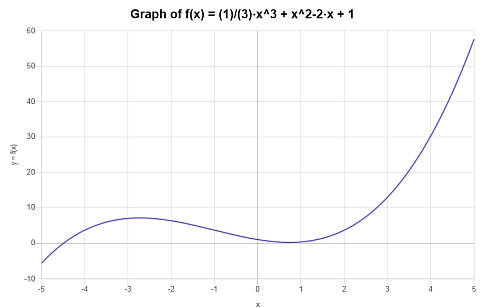
निम्नलिखित बहुपद को ग्राफ करें: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

तमाम: हमें निम्नलिखित बहुपद अभिव्यक्ति के साथ प्रदान किया जाता है, जिसकी हमें गणना करने की आवश्यकता है: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\)।

प्रदान की गई अभिव्यक्ति IRREDUCIBLE है, इसलिए सरल बनाने के लिए कुछ भी नहीं है।

निम्नलिखित भूखंड अंतराल पर दिए गए बहुपद अभिव्यक्ति के लिए प्राप्त किया जाता है \([-5, 5]\):

उदाहरण: बहुपद ग्राफ

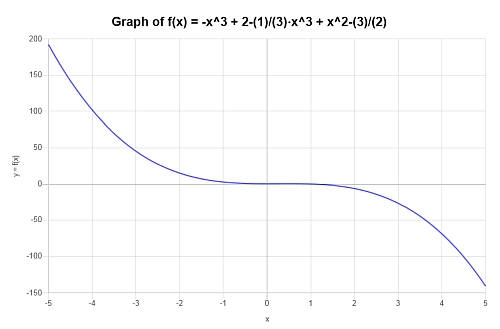
सरल और ग्राफ: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

तमाम: अब, हमें साथ काम करने की आवश्यकता है: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\)।

निम्नलिखित सरलीकरण प्राप्त किया जाता है:

\( \displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\)

Grouping the terms with \(x^3\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(-1-\frac{1}{3}\right)x^3+x^2+2-\frac{3}{2}\)

Grouping together numerical values and fractions and simplifying those terms that were grouped with \(x^3\)

\( \displaystyle = \,\,\)

\(\displaystyle -\frac{4}{3}x^3+x^2+2-\frac{3}{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle 2-\frac{ 3}{ 2}=2 \times \frac{ 2}{ 2}-\frac{ 3}{ 2}=\frac{ 2 \times 2-3}{ 2}=\frac{ 4-3}{ 2}=\frac{ 1}{ 2}\)

\( \displaystyle = \,\,\)

\(\displaystyle x^2+-\frac{4}{3}x^3+\frac{1}{2}\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle = \,\,\)

\(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\)

जो बहुपद सरलीकरण की प्रक्रिया का समापन करता है।

तो फिर, निम्नलिखित भूखंड \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) के लिए प्राप्त किया जाता है अंतराल पर \([-5, 5]\):

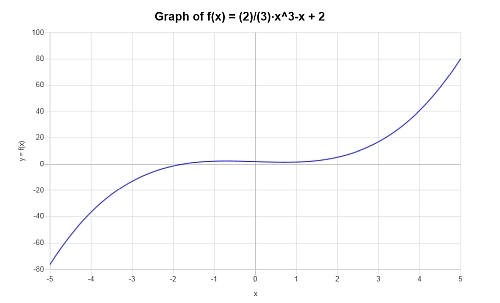
उदाहरण: अधिक बहुपद रेखांकन

निम्नलिखित बहुपद \( p(x) = \frac{2}{3} x^3 - x +2 \) का ग्राफ खोजें।

तमाम: इस उदाहरण के लिए, प्रदान किया गया बहुपद है: \(\displaystyle \frac{2}{3} x^3 - x +2 \)।

इस मामले में, प्रदान की गई अभिव्यक्ति अप्रासंगिक है, इसलिए सरल बनाने के लिए कुछ भी नहीं है।

अधिक बहुपद कैलकुलेटर

बहुपद को रेखांकन करना बेहद उपयोगी है क्योंकि यह हमें उनकी जड़ों और उनके अंतिम व्यवहार के आसपास उनके व्यवहार की मुख्य विशेषताओं को दर्शाता है।रेखांकन आमतौर पर लगभग जहां जड़ हो सकता है, वहां की पहचान करने के साथ हाथ से हाथ में जाता है, जिसका उपयोग किया जा सकता है तंग भी।

यद्यपि हम बहुपद के बारे में बहुत कुछ जान सकते हैं, लेकिन इसे रेखांकन करने से, हमें अभी भी प्रयास करने की प्रक्रिया से गुजरने की आवश्यकता है सरायस अयस्क नल के लिए शुरुआती बिंदु के रूप में अफ़स्या 2 से अधिक डिग्री के साथ (यह, जो नहीं हैं तमाम )।

व्यवस्थित रूप से अनुमान लगाना या तर्कसंगत जड़ों को ढूंढना, उपयोग के साथ जोड़ा गया तमाम या अफ़रप तो उपयोग करने के लिए तमाम की एक सफल खोज हो सकती है बहुपद जड़ें , लेकिन इस तरह का दृष्टिकोण हमेशा काम नहीं करता है, और अक्सर आपको संख्यात्मक अनुमानों को खोजने के लिए कैलकुलेटर पर भरोसा करने की आवश्यकता होती है।