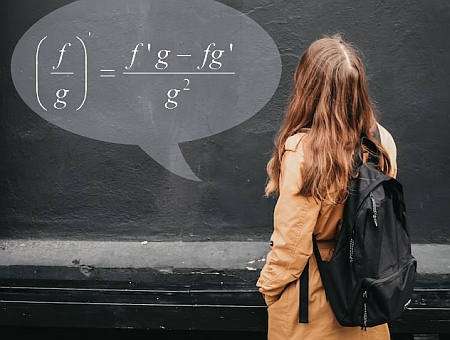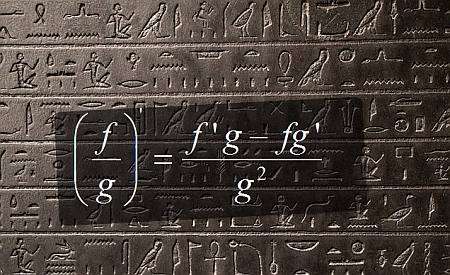قاعدة الحاصل
ستسمح لك هذه الآلة الحاسبة باستخدام قاعدة الحاصل لوظيفة تتضمن حاصلًا , مما يوضح جميع خطوات العملية.كل ما تحتاجه لتوفيره هو وظيفة قابلة للتمييز صالحة.تحتاج هذه الوظيفة إلى إشراك حاصل واحد على الأقل من أجل تطبيق قاعدة الحاصل.
مثال على وظيفة صالحة سيكون f (x) = (x^2 + 2x + 1)/(x^2-1) , أو شيء مثل f (x) = sin (x)/x , إلخ.
بمجرد توفير وظيفة صالحة تتضمن اقتباسات , يجب عليك النقر فوق الزر "حساب" للحصول على خطوات الحساب الموضحة.
جنبا إلى جنب مع
سيدا
و
قaudة السلم
, ال
قaudة alحaصl
هي واحدة من أهم الأساسي
قoaudd amشtقة
وبعد
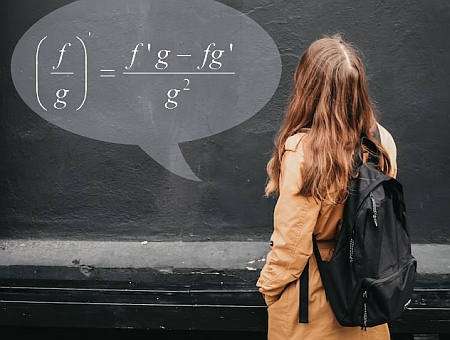
صيغة قاعدة الحاصل
بعبارات بسيطة ,
قaudة alحaصl
يساعدك على حساب مشتق الحاصل , باستخدام معرفة الوظائف الفردية ومشتقاتها.صيغة قاعدة الحاصل هي:
\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]
ما هي خطوات استخدام قاعدة الحاصل؟
-
الظهر 1:
حدد بوضوح الوظائف f (x) و g (x) التي تدخل في البسط والمقام من الحاصل
-
ال alخطoة 2:
تبسيط أي مصطلح واضح يمكن تبسيطه
-
الله 3:
احسب المشتقات المقابلة F '(x) و g' (x)
-
الظهر 4:
قم بتوصيل القيم الموجودة في الخطوة 3 في الصيغة \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)
لاحظ أن F (x) و g (x) قد لا تزال وظائف معقدة , لذلك قد تحتاج إلى استخدام قواعد أخرى مثل قاعدة السلسلة لحساب كل من F '(x) و g' (x).
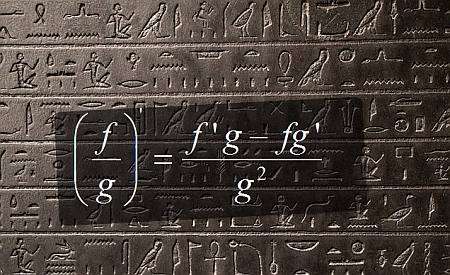
مشتق القاعدة الحاصل
عند حساب مشتق قاعدة الحاصل , فأنت تقلل من مشتق الحاصل على معرفة المشتقات الفردية , لكن تلك المشتقات الفردية قد لا تزال تتطلب العديد من الخطوات معها
chalقoadad chlmشtقة
لكى تحل.
هذا هو السبب في اعتبار التمايز عملية "واضحة" , ولكن لا يزال , تحتاج إلى تنظيم بما فيه الكفاية وتتبع جميع القطع التي تنشأ عند التحلل مع القواعد المشتقة , ثم تابع القطع الأصغر التي قد تتطلب المزيد من قواعد التمايزمُطبَّق.
لذلك قد ينتهي بك الأمر بعملية تكرارية , ولكن من المضمون أن تنتهي في مرحلة ما عن طريق التعمق في كل جزء أصغر , حتى تجد مشتقًا أوليًا , مثل أ
مادين الدعود
أو أ
mشtق ثlaثyة
وبعد
قاعدة الحاصل في التمايز
دور
قaudة alحaصl
من المهم جدًا , وهو سبب وجيه لترغب في استخدام آلة حاسبة لذلك.من الناحية الجبرية , يمكن اعتبار قاعدة الحاصل معقدة أكثر من قاعدة المنتج , وقد يكون هذا صحيحًا في العديد من الحالات , ولكنه يعتمد في النهاية على تعقيد الوظائف في البسط والمقام.

أمثلة قاعدة الحاصل
النظر في الوظيفة: \(f(x) = \frac{x^2+1}{x-2}\) , ابحث عن مشتقها.
الملم:
على سبيل المثال , نحتاج إلى تحليل الوظيفة \(\displaystyle f(x)=\frac{x^2+1}{x-2}\) , من حيث العثور على مشتقها.
\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)
By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)
By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)
Since the derivative of a constant is 0, we get that:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)
We already know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)
In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)
Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)
Removing unnecessary parentheses and multiplying the terms by \(-1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)
Aggregating those terms with \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)
Putting together the numerical values and operating the terms that were grouped with \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)
تاسنتا
: نجد أن مشتق الوظيفة المحددة هو:
\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]
إذن , فإن التصوير الرسومي للوظيفة ومشتقها هو \([-5, 5]\):
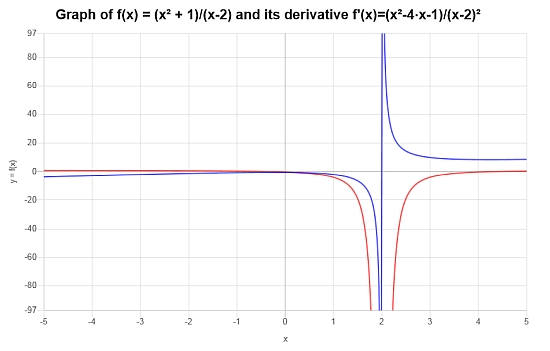
مثال: حساب قاعدة الحاصل
الآن ضع في اعتبارك \(f(x) = \frac{x}{\sin(x)}\) , ابحث عن مشتقها باستخدام قاعدة الحاصل.
الملم:
لهذا المثال الثاني , فإن الوظيفة التي يهمنا هي \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\).دعونا نميزه باستخدام قاعدة الحاصل.
\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)
Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
We already know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)
By reorganizing/simplifying/expanding the terms that are amenable to
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
تاسنتا
: الاستنتاج هو أنه , بناءً على الحساب أعلاه , يتم إعطاء المشتق بواسطة:
\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]
بيانياً , يمكننا أن نرى الوظيفة (باللون الأزرق) ومشتقها (باللون الأحمر):
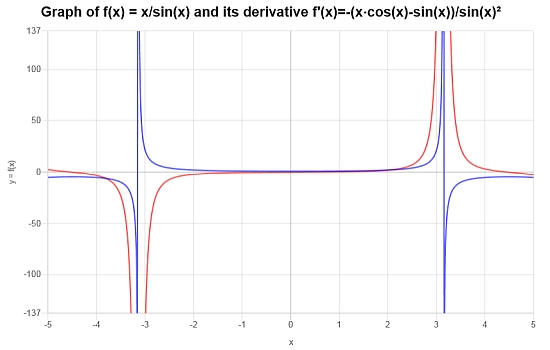
المزيد من أمثلة قاعدة الحاصل
أخيرًا , ضع في اعتبارك الوظيفة: \(f(x) = \frac{\sin(x)}{x^2}\) , ابحث عن مشتقها.
الملم:
بالنسبة لقاعدة الحاصل النهائية هذه , نعمل مع الوظيفة \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\)..
\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)
The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)
We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)
By simplifying and regrouping terms
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)
تاسنتا
: للوظيفة المحددة , مشتقها هو:
\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]
يوضح الرسم البياني أدناه الموقف لـ \(f\) و \(f'\):
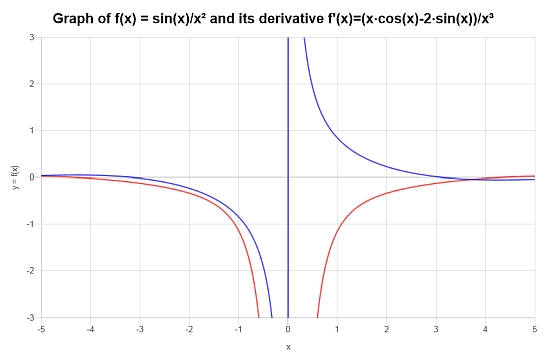
المزيد من الحاسبة المشتقة
في حساب التفاضل والتكامل سوف
العرف
في كل مكان تنظر إليه.هناك الآلاف من التطبيقات التي تنطوي عليها صنعها على أهم الأدوات للعلوم والهندسة.
ستحتاج إلى التعرف على
العداد
بالنسبة للتطبيقات المختلفة غالبًا ما تتضمن معدلات ذات صلة , أو في حساب التفاضل والتكامل متعدد المتغيرات , سترغب في اهتمامك
الهاور علا
وبعد
بشكل عام , ستجد حياتك أسهل عند التعامل مع المشتقات إذا كنت قادرًا على التعامل بشكل صحيح مع الأكثر شيوعًا
قoaudd amشtقة
, بما في ذلك
قaudة السلم
, وكذلك
سيدا
و
قaudة alحaصl
وبعد