المحللين حساب التفاضل والتكامل

حاسبة خط الظل

عاليمت: استخدم هذه الآلة الحاسبة لحساب خط الظل لوظيفة معينة , عند نقطة معينة , توضح جميع الخطوات.يرجى كتابة الوظيفة والنقطة المقابلة في مربع النموذج أدناه.

حول حاسبة خط الظل هذا

ستسمح لك هذه الآلة الحاسبة بإجراء الحسابات المطلوبة بسلاسة للحصول على خط الظل للوظيفة , عند نقطة معينة , مما يوضح جميع الخطوات.

كل ما عليك فعله هو توفير وظيفة صالحة f (x) , والنقطة التي تريد فيها خط الظل في.يمكن أن تكون الوظيفة أي وظيفة صالحة , قابلة للتفاضلت مثل f (x) = sin (x) , أو f (x) = x^2 - x + 1 , إلخ. يمكن أن تكون النقطة أي تعبير رقمي صالح , مثل 1/2مثال.

بعد ذلك , عندما يتم توفير المعلومات المطلوبة , وهي صالحة , تحتاج إلى النقر على "حساب" للحصول على جميع خطوات معادلة خط الظل الموضحة لك.

تطبيقات خط الظل في العلم في كل مكان.أيضا يسمى الفتاة , لها معنى عميق حقًا في الفيزياء والهندسة , حيث تكون فكرة المساهمة الرئيسية في التغيير (الجزء الأول) هي التي تكشف عنها الكثير من المعلومات حول العملية.

ما هو خط الظل

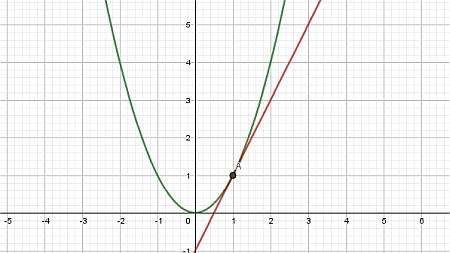
بعبارات بسيطة , فإن خط الظل هو خط يتقاطع مع المنحنى , لكنه يتقاطع عليه عند نقطة واحدة فقط (على الأقل محليًا).يتم إنشاء خط الظل هذا عن طريق إصلاح نقطة \(x_0\)ثم أخذ نقطة مختلفة \(x_1\).

ثم , من خلال بناء الخط الذي يمر عبر النقاط \((x_0, f(x_0))\)و \((x_1, f(x_1))\), نحصل على ما يسمى أ خط قaطud , كما هو موضح في الرسم البياني أدناه:

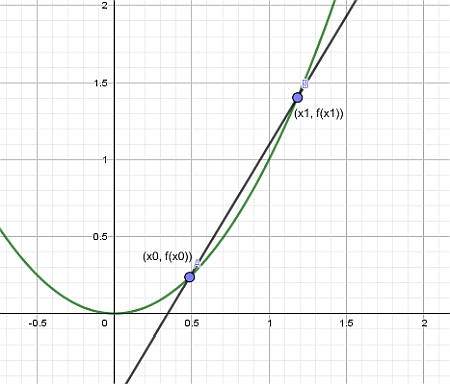
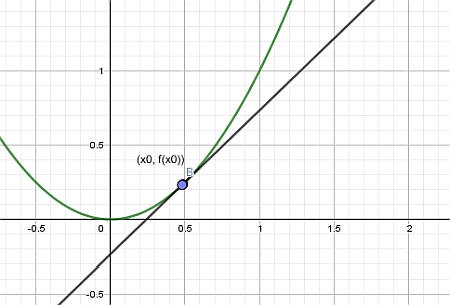
أخيرًا , سمحنا لنهج \(x_1\)إلى \(x_0\), وما نحصل عليه هو خط الظل:

خطوات لإيجاد خط الظل هندسيًا

الظهر 1: حدد الوظيفة F (x) التي تريد العمل معها , والنقطة X0.أنت بحاجة إلى كلاهما
ال alخطoة 2: ستكون النقطة (x0 , f (x0)) على منحنى الدالة f (x).ارسمها
الله 3: اختر نقطة (x1 , f (x1)) , لـ x1 التي تختلف عن x0 (يمكن أن تكون إلى اليسار أو اليمين من x).ارسمها
الظهر 4: ارسم خطًا يمر عبر النقاط (x0 , f (x0)) و (x1 , f (x1))
الظهر 5: اختر نقطة X2 التي تكون في منتصف الطريق بين X0 و X1 , ورسم خطًا يمر عبر النقاط (X0 , F (x0)) و (x2 , f (x2))
ال 6: كرر هذه العملية عدة مرات

ستساعدك هذه الطريقة الرسومية في الحصول على فكرة تقريبية عن كيفية ظهور خط الظل , ولكنه تقريبًا (ما لم تكن الوظيفة F (x) خطية).

صيغة خط الظل

يمكن أن تمنحك طريقة التقريب التي تستخدم خطوط Secant فكرة عما تبحث عنه , ولكن لحسن الحظ , هناك صيغة دقيقة لحساب خط الظل إلى وظيفة عند نقطة \(x_0\).صيغة خط الظل هي:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

بسيطة , هاه؟بعبارات بسيطة , هذه الصيغة تخبر أن خط الظل هو الله الله \((x_0, f(x_0))\)وهذا يحتوي على منحدر من\(m = f'(x_0)\)

بعد ذلك , بعبارات سهلة , يكون ميل خط الظل في نقطة معينة هو بالضبط مشتق الوظيفة في تلك المرحلة.

خطوات لتطبيق صيغة خط الظل

الظهر 1: حدد الوظيفة F (x) والنقطة x0
ال alخطoة 2: حساب قيمة الوظيفة في X0 , وهي F (x0)
الله 3: حساب مشتق F (x) في النقطة x0 , لذلك تحتاج f '(x0)
الظهر 4: قم بتطبيق صيغة خط الظل مباشرة \(y = f(x_0) + f'(x_0) (x - x_0)\)

بمجرد حصولك على ماعد الله , يمكنك تحويله إلى تنسيق أنه مفيد للغاية للموقف في متناول اليد.

ميل خط الظل

واحدة من الوجبات الرئيسية هي أن ميل خط الظل في \(x_0\)هو بالضبط \(f'(x_0)\), وهو المشتق في النقطة \(x_0\).يوفر هذا تفسيرًا واضحًا ومفيدًا للغاية للمشتق من الناحية الهندسية.

يسمح هذا الاتصال بإيجاد معادلة خط الظل إلى منحنى معين عند نقطة معينة من خلال النظر إلى مشتق الوظيفة.

متى لديك خط الظل الأفقي؟

سيحدث خط الظل الأفق عندما يكون النقطة التي تم اختيارها \(x_0\) عندما يكون المشتق المقابل في تلك المرحلة يساوي الصفر.في هذه الحالة , سيكون خط الظل (وهو الخط الذي يمس المنحنى عند نقطة واحدة محليًا) موازية للمحور ص.

لذلك , كل ما تحتاج إلى معرفته من أجل تحديد خطوط الظل الأفقية هو إيجاد نقاط يكون فيها مشتق الوظيفة صفرًا.

متى يكون لديك خط الظل العمودي؟

سيحدث خط الظل العمودي عندما يكون المشتق "لا حصر له" في مرحلة ما.هذه طريقة بسيطة للقول إن هذا هو المكان الذي لا يتم فيه تعريف المشتق في نقطة معينة , ولكنه يتقارب مع Infinite مع اقترابنا من هذه النقطة.

على سبيل المثال , يمكن للمرء أن يقول أن \(f(x) = \frac{1}{x}\) لديه خط الظل العمودي عند x = 0. على الرغم من أنه يمكن القول أنه لا يوجد خط الظل لأن المشتق غير محدد جيدًا عند x = 0.

مثال: خط الظل

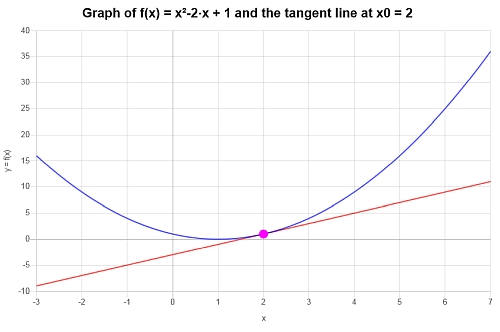
ابحث عن معادلة خط الظل لـ \(f(x) = x^2 - 2x + 1\), عند النقطة \(x_0 = 2\).

إل: الوظيفة التالية هي تلك التي نحتاج إلى العمل معها: \(\displaystyle f(x)=x^2-2x+1\).أولاً , نحتاج إلى حساب مشتقها.

جاءت الوظيفة مبسطة بالفعل , حتى نتمكن من المتابعة مباشرة لحساب مشتقها:

\( \displaystyle \frac{d}{dx}\left(x^2-2x+1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-2x+1 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\)

Since the derivative of a constant is 0, we find that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)\)

Directly we get: \(\frac{d}{dx}\left( 2x \right) = 2\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2\)

خط alظl : معادلة خط الظل للدالة \(\displaystyle f(x)=x^2-2x+1\) في النقطة \(x_0 = 2\) هي:

\[y = y_0 + f'(x_0)(x - x_0) \]

في هذه الحالة , يؤدي \(\displaystyle y_0 = f(x_0)\), لذا فإن توصيل قيمة النقطة \(x_0 = 2\)في الدالة يؤدي إلى:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

أيضا , توصيل قيمة النقطة \(x_0 = 2\) في المشتق المحسوب يؤدي إلى:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

إذن , نقوم الآن بتوصيل هذه القيم في صيغة خط الظل للحصول على:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

خatmة : لذلك , وجد أن خط الظل للدالة \(\displaystyle f(x)=x^2-2x+1\) في النقطة \(x_0 = 2\) هو:

\[y = 2x-3 \]

يتم الحصول على المؤامرة التالية للوظيفة المحددة وخط الظل الخاص بها في \(x_0 = 2\):

مثال: معادلة خط الظل

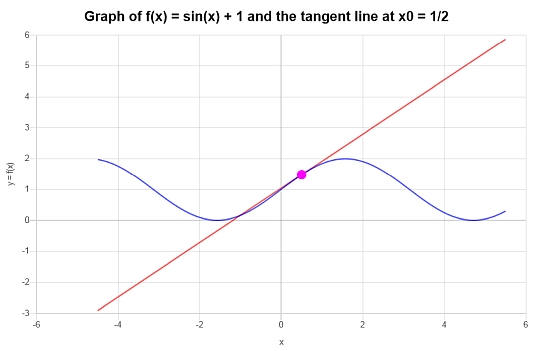
ما هو خط الظل في x = 1/2 , للوظيفة \(f(x) = \sin(x) + 1\)؟

حل:

تم توفير الوظيفة التالية: \(\displaystyle f(x)=\sin\left(x\right)+1\), والتي نحتاج إلى حساب مشتقها.

جاءت الوظيفة مبسطة بالفعل , حتى نتمكن من المتابعة مباشرة لحساب مشتقها:

\( \displaystyle \frac{d}{dx}\left(\sin\left(x\right)+1\right)\)

By linearity, we know \(\frac{d}{dx}\left( \sin(x)+1 \right) = \frac{d}{dx}\left(\sin(x)\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)+\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \cos\left(x\right)\)

خط alظl : نجد أن المعادلة المقابلة لخط الظل في النقطة \(x_0 = \frac{1}{2}\) تعطى:

\[y = y_0 + f'(x_0)(x - x_0) \]

ولكن في هذه الحالة المحددة , \(\displaystyle y_0 = f(x_0)\), مما يعني أننا نحتاج إلى توصيل قيمة النقطة \(x_0 = \frac{1}{2}\)في الوظيفة , حتى نحصل على:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

الآن , فعل الشيء نفسه في المشتق , لـ \(x_0 = \frac{1}{2}\) نجد

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

الآن نحتاج فقط إلى توصيل القيم , لذلك نجد ذلك

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

خatmة : نجد أن خط الظل المقابل الذي نبحث عنه , في النقطة المقابلة \(x_0 = \frac{1}{2}\) يتم تقديمها بواسطة

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

بيانياً:

مثال: خط الظل آخر

ما هو خط الظل في x = 0 , للدالة \(f(x) = \cos(x)\)؟هل هذه النتيجة منطقية؟

إل: لاحظ أن \(f'(x) = -\sin(x)\), إذن ثم \(f'(0) = -\sin(0) = 0\).هذا هو أن خط الظل لديه ميل من m = 0 عند x = 0 , لذلك فإن معادلة خط الظل هي ببساطة \(y = y_0 = \cos(0) = 1\).هذا أمر منطقي لأنه في هذه الحالة , خط الظل هو خط أفقي.

مزيد من الحاسبة التمايز

قد يزعم بعض الناس أن التمايز هو تمرين مباشر نسبيًا , وأن باستخدام أ حaSbة mشtقة قد لا تكون هناك حاجة , ولكن في الحقيقة , يمكن أن يكون حساب المشتقات مرهقًا إلى حد ما وقد يتطلب فترة طويلة الإسبابت العنب .

عندما يكون لديك تعبير مع أكثر من متغير واحد , من أجل العثور على المشتق , ستحتاج إلى تحديد ما إذا كانت المتغيرات مستقلة عن بعضها البعض , وفي هذه الحالة تستخدم الملمس , أو إذا كانت هناك معادلة تربط المتغيرات في هذه الحالة ستحتاج إلى استخدامها العداد .

المجالان الرئيسيان في حساب التفاضل والتكامل التفاضلي هما التكامل والتمايز , وكلاهما له تطبيقاتهما الواسعة , في كل مكان. الملمس تظهر بطول كبير في تطبيقات الهندسة والاقتصاد.

من ناحية , يتعامل التمايز مع معدلات التغيير غير المألوفة , في حين أن التكامل يتعامل مع تلخيص معدلات التغيير اللانهائية , وهكذا , ترتبط ارتباطًا وثيقًا من قبل آلنجى الإثارة .