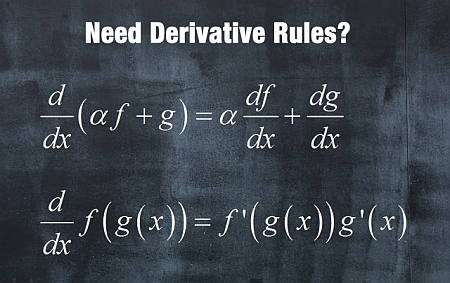حول القواعد المشتقة
ستسمح لك هذه الآلة الحاسبة بحساب مشتق الوظيفة التي تقدمها من خلال تطبيق قواعد التمايز الأساسية المطلوبة , وإظهار جميع خطوات العملية , مع الإشارة إلى مكان تطبيق كل قاعدة.
تحتاج فقط إلى توفير وظيفة صالحة يمكن اختلافها (مما يعني أن لديها مشتقًا).على سبيل المثال , يمكن أن تكون وظيفة صالحة f (x) = 1/3*x*sin (x) , فقط لذكر مثال واحد.
بعد ذلك , عندما تكون قد كتبت وظيفتك بالفعل , يمكنك فقط النقر فوق "حساب" للحصول على جميع خطوات التمايز المعروضة.
إن بساطة قواعد المشتقات تجعل عملية التمايز التي يتم الاعتراف بها على أنها "سهلة" , وهو حكم ربما يكون مبالغة.
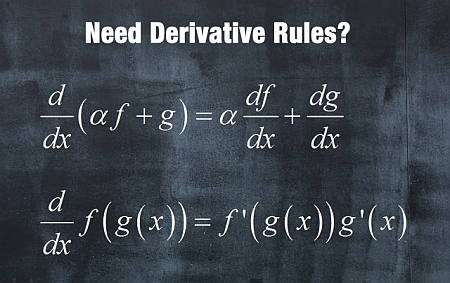
القواعد المشتقة الأساسية
هناك أربع قواعد مشتقة أساسية لتتعلمها
-
قaudة alخطiة:
للوظائف \(f(x)\) و \(g(x)\) , وثابتة \(a\) , فإن المشتق هو عملية خطية: \((af(x)+g(x))' = af'(x)+g'(x)\)
-
سيدا
للوظائف \(f(x)\) و \(g(x)\) , مشتق المنتج هو \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
-
قaudة alحaصlh:
للوظائف \(f(x)\) و \(g(x)\) , مشتق الحاصل هو \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
-
قaudة السلم
للوظائف \(f(x)\) و \(g(x)\) , مشتق الدالة المركب هو \((f(g(x)))' = f'(g(x))g'(x)\)
ستعمل هذه القواعد مثل السحر وستساعدك في العثور على مشتق أي وظيفة أساسية.
كيفية استخدام القواعد المشتقة؟
-
الظهر 1:
حدد الوظيفة f (x) التي تريد التمييز , تبسيط إذا لزم الأمر
-
ال alخطoة 2:
حاول تقسيم الوظيفة إلى أجزاء مشتقة أصغر , باستخدام الخطية
-
الله 3:
اعتمادًا على بنية الوظيفة F (x) , استخدم أيًا من القواعد المتاحة (قاعدة المنتج , الحاصل والسلسلة) , وكن على علم بأنك قد تحتاج إلى تطبيق العديد من القواعد على التوالي)
عادةً ما ينتهي بك الأمر بمجموعة من قواعد التمايز , حتى تصل إلى النقطة التي تجد فيها وظيفة أولية , تعرفها بالفعل كيفية التمييز.

هل يمكنني حل جميع المشتقات
إن القول بأن استخدام قواعد التمايز يمكن أن يؤدي بك إلى حل جميع المشتقات يمكن أن يكون مبالغة.ستكون قادرًا على حل معظم المشتقات , وبالتأكيد جميع المشتقات الأساسية , ولكن هناك وظائف لها سلوك أقل سهولة يمكن تعريفه , على الرغم من أنها لا يتم التعامل معها عادة في دورات حساب التفاضل والتكامل الأساسية.
بالنسبة للوظائف الأساسية المعنية , سيتم تمييز معظمها دون مشكلة.
أ
mشtق قaudة hlmnatج
ب
mشtق alقaudة alحaصl
أو
mشtق قaudة السلم
من غير المرجح أن تكون في عزلة , ومن المحتمل أن تأتي في سلسلة من القواعد العديدة التي يجب استخدامها معًا.

مثال: قواعد مشتقة
باستخدام القواعد المشتقة الأساسية , قم بحساب المشتق التالي: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)
الملم:
دعونا نفكر في الوظيفة المعطاة التالية التي يحتاج المشتق من أجلها \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)
لا تحتاج الوظيفة إلى تبسيط , حتى نتمكن من الذهاب مباشرة إلى حساب مشتقها:
\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)
Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)
We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)
By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)
But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)
And finally, grouping the terms together
\( \displaystyle = \,\,\)
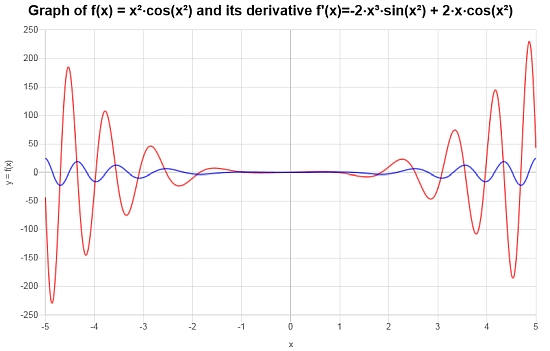
\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)
يظهر الرسم البياني المقابل للوظيفة ومشتقها أدناه:
مثال: المزيد من القواعد المشتقة
حساب المشتق التالي: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) باستخدام القواعد المشتقة الأساسية.
الملم:
الآن , المهمة المطروحة هي التمييز بين الوظيفة \(\displaystyle f(x)=x\cos\left(x^2+1\right)\)
\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)
In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)
The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)
Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)
Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)
مثال على القواعد المشتقة
للوظيفة \( f(x) = (x-1)(x^2+1) \) , استخدم القواعد المشتقة لإيجاد مشتقها.
الملم:
For this final example, we need to differentiate: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\).
خطoة أolelyة:
في هذه الحالة , نحتاج أولاً إلى توسيع الوظيفة المحددة \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \) , ومن أجل القيام بذلك , نقوم بإجراء خطوات التبسيط التالية:
\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)
Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle x^3-x^2+x-1\)
بعد توسيع الوظيفة , يمكننا المتابعة إلى حساب المشتق:
\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)
By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)
We know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)
Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)
\( \displaystyle = \,\,\)
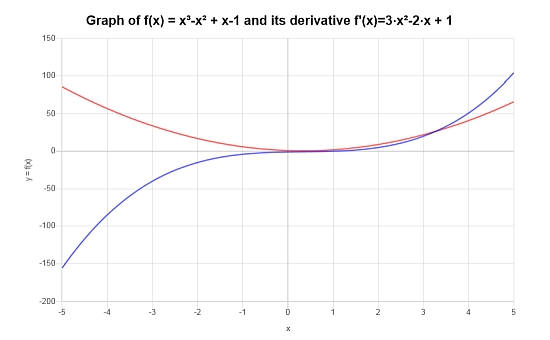
\(\displaystyle 3x^2-2x+1\)
بيانياً , هذه هي الطريقة التي تبدو بها الوظيفة ومظهرها المشتق:
المزيد من الحاسبة المشتقة
أحد السحر حول التمايز هو أنه يمكنك
الهاور على الله
من أي وظيفة باستخدام بعض القواعد الأساسية والبسيطة , بما في ذلك
سيدا
ب
قaudة alحaصl
وبطبيعة الحال ,
قaudة السلم
.عادة ما يكون هذا الترسانة الصغيرة كافية لحساب أي مشتق تحتاجه
التمايز والتكامل هما الممرات الرئيسية في حساب التفاضل والتكامل , دون أي نزاع , لأنها مركز العديد من التطبيقات , في جميع جوانب العلوم.من المعدلات ذات الصلة إلى
الاشتقاق الضمني
, مع
الملمس
في الفيزياء والاقتصاد