المحللين حساب التفاضل والتكامل

حاسبة التمايز الضمنية

عاليمت: استخدم حاسبة التمايز الضمنية هذه لحساب المشتق \(\frac{dy}{dx}\), عندما يتم ربط \(x\)و \(y\)عبر معادلة.توفير معادلة تتضمن x و y في مربع النموذج أدناه.

الاشتقاق الضمني

ستساعدك هذه الآلة الحاسبة على إجراء تمايز ضمني لمعادلة تتضمن المتغيرات X و Y.تحتاج إلى توفير معادلة صالحة مثل x^2 + y^2 = 1 , أو xy - x^2 y^2 = 0 , إلخ.

بمجرد تقديم معادلة صالحة تتضمن متغيرين (\(x\)و\(y\)) , كل ما عليك فعله هو النقر على الزر "حساب" , وسيتم عرض جميع خطوات التمايز الضمني المقابل.

هذا ال حASBة dy/dx maud خطoat بمعنى أنه سيظهر لك جميع الخطوات ذات الصلة لحساب مشتق متغير واحد فيما يتعلق بآخر , طالما أن هذين المتغيرين يرتبطان في معادلة واحدة.هذه العلاقة هي ما يسمح لك بالعثور على المقابلة Mشtق ضmny .

إن وجود معادلة تتعلق بالمتغيرين \(x\)و \(y\)يخبرنا أنه ينبغي لنا أن نكون قادرين على التعبير عن \(y\)كدالة لـ \(x\)وكتابة \(y = y(x)\).في كثير من الأحيان , لا يمكننا التعبير صراحة \(y\)كدالة لـ \(x\)نحن نفترض أن هناك هذه الوظيفة , وفي هذه الحالة , من المنطقي التمييز بين \(y\)فيما يتعلق بـ \(x\).

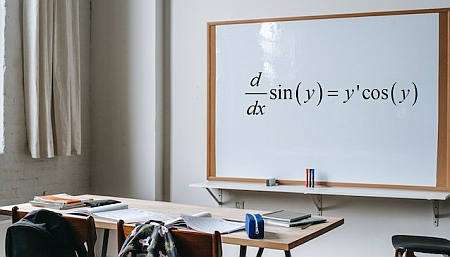
ما هو التمايز الضمني؟

التمايز الضمني هو ح ساب آماي تقنية بناءً على افتراض أنه من الممكن أن نوضح من معادلة معينة تتضمن \(x\) و \(y\) أن \(y\) هي وظيفة \(x\) على الرغم من أن الأوقات في كثير من الأحيان لا يمكننا كتابة هذه الوظيفة بشكل صريح.

بمجرد إجراء هذا الافتراض , نفترض أنه يمكننا حساب \(\frac{dy}{dx}\) ويمكننا استخدام جميع المعروفة قoaudd amشtقة (( سيدا و قaudة alحaصl و قaudة السلم ) للتمييز بين جانبي المعادلة , وحل \(\frac{dy}{dx}\).

ما هي طريقة التمايز الضمنية؟

طريقة التمايز الضمنية هي طريقة تسمح لك بحساب مشتق إلى التعبيرات التي لا يتم وضعها مباشرة بتنسيق \(f(x)\).هذا , عندما يتم إعطاء دالة لمتغير \(x\) على سبيل المثال , نحن ببساطة نمضي قدمًا ونميز هذه الوظيفة.

ولكن عندما يرتبط متغيران \(x\) و \(y\) من خلال معادلة , مثل \(x^2+y^2 = 1\) على سبيل المثال , يمكنك أيضًا التمييز بين y فيما يتعلق بـ x , بموجب الطريقة التقليدية , ستحتاج إلى حل y من حيث x ,وبعد ذلك يمكنك التمييز.

باستخدام تمايز ضمني , يمكنك التمييز مباشرة , من خلال افتراض أن \(y = y(x\), والاستفادة من قaudة السلم .

خطوات لاستخدام التمايز الضمني

الظهر 1: تحديد المعادلة التي تنطوي على متغيرين x و y.تبسيط أي شروط زائدة
ال alخطoة 2: افترض أن y هي وظيفة x , y = y (x) , لذلك من المنطقي حساب مشتق y فيما يتعلق بـ x
الله 3: حSAB الجهادية من كلا جانبي المعادلة باستخدام كل قoaudd amشtقة انت تحتاج.سيؤدي ذلك إلى وجود مساواة تكون فيها x و y و y '
الظهر 4: حل ما حصلت عليه في الخطوة 3 من أجل y.لاحظ أنه سيتم كتابة Y 'عادةً كدالة لـ x و y , وهو أمر جيد , لأن y يعتمد أيضًا على x

هذه منهجية عامة للغاية , وسيكون لها تفاصيل دقة من حالة إلى أخرى , ولكن هذه هي المخططات التي يجب أن تعمل في معظم الحالات , مع صعوبة التلاعب الجبري المحتملة.

لماذا استخدام آلة حاسبة تمايز ضمنية

يمكن أن يكون التمايز الضمني مربكًا في بعض الأحيان , إذا لم تكن واضحًا جدًا بشأن ما تميز , واحترام المتغير.ستساعدك الآلة الحاسبة في مقارنة النتيجة الخاصة بك , وشيء خاص واحد في الآلة الحاسبة لدينا هو أن جميع خطوات العملية تظهر.

هذه مساعدة حاسمة لك , لأنها ستظهر لك تمامًا القاعدة المشتقة , ومكان تطبيقها.

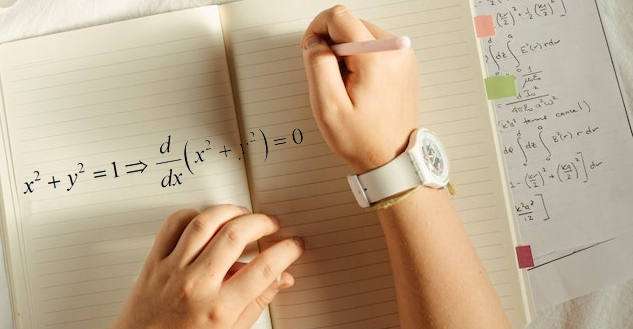
ما هي الهدف من التمايز الضمني؟

هذا هو السؤال عادلة.إذا كان لديك معادلة تتضمن X و Y , فلماذا لا تحل Y من حيث X واستخدام حساب مشتق منتظم للحصول على مشتق Y فيما يتعلق بـ X.يمكنني أن أعطيك سببين وجيدين على الأقل:

السربب 1: قد يكون هذا هو أنه لا يمكنك حل y من حيث x بشكل صريح.قد تكون هناك وظيفة , لكن لا يمكنك العثور عليها ببساطة.فكر في y + tan (y) = x^2
السبح 2: حتى لو حدثت ح y فymylح x , قد يكون تعبيرًا معقدًا حقًا , وقد يكون حساب المشتقات معقدًا وصعبًا للغاية.عادة , التمايز الضمني بسيط من الناحية الجبرية , من الناحية النسبية

هل يعتمد المشتق الضمني على y؟

ليس دائما , ولكن في كثير من الأحيان.الآن , هذا يقول فقط أن \(\frac{dy}{dx}\) يمكن أن يعتمد على x و y , ولكن بما أن y يعتمد على x , فإنه يقول أنه كما هو متوقع \(\frac{dy}{dx}\) يعتمد على x.

سيتم تقديم أمثلة تمايز ضمنية مختلفة في القسم التالي.

المشتق الضمني الثاني

سؤال واحد هو: هل يمكن حساب المشتق الثاني باستخدام التمايز الضمني؟الجواب نعم.أنت فقط تفعل الشيء نفسه كما هو الحال مع المشتق الأول باستخدام التمايز الضمني , فأنت تفترض ببساطة أن \(y\)هي وظيفة \(x\), لذلك تكتب \(y = y(x)\), ويمكنك التمييز بقدر ما تريد.

على سبيل المثال , قل أنك تريد العثور على \(\frac{d^2y}{dx^2}\)بالنظر إلى المعادلة \(x^2+y^2=1\).التمييز بين الجانبين فيما يتعلق بـ \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

الآن , تميز مرة أخرى فيما يتعلق بـ X:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

والآن نقوم بحل \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

مثال: مثال تمايز ضمني

البحث عن \(\frac{dy}{dx}\)للمعادلة: \(x^2 - y^2 = 2y\)

إل: هذا مثال على التمايز الضمني.تم توفير المعادلة التالية: \(\displaystyle x^2-y^2=2y\), والتي نحتاج إلى إجراء تمايز ضمني , حيث نفترض أن \(y\)هي وظيفة \(x\).

لا تحتاج المعادلة إلى مزيد من التبسيط , حتى نتمكن من المتابعة مع التمايز الضمني:

نحتاج إلى التمييز بين جانبي المعادلة فيما يتعلق بـ \(x\), وعلى كلا الجانبين نفترض أن \(y = y(x)\).

الله عليه : التمييز بين الجانب الأيسر فيما يتعلق بـ \(x\)

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

العداد : التمييز بين الجانب الأيمن فيما يتعلق بـ \(x\)

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

لذلك , يتم الحصول على ما يلي بعد التمييز بين الجانبين فيما يتعلق بـ \(x\):

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

وضع كل المصطلحات على جانب واحد:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

تجميع كل ما يحتوي على \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

أخيرًا , يؤدي حل \(\displaystyle \frac{dy}{dx}\), إلى:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

مثال: حسابات التمايز الأكثر ضمنيا

ما هو ميل خط الظل إلى دائرة الوحدة عند النقطة \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)

إل: لاحظ أن معادلة وحدة الوحدة هي \(\displaystyle x^2 + y^2 = 1\), والتي تحدد ضمنيًا \(y\)كدالة لـ \(x\).من أجل العثور على خط الظل , نحتاج إلى حساب \(\frac{dy}{dx}\) في النقطة المحددة.باستخدام التمايز الضمني , فإننا نفرق جانبي المعادلة التي تحدد دائرة الوحدة: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\]xyzg \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

nقطة alahtamam hey \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), إذn.

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Heذaa yueny أn myl خط alظl فy alnقطة \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)ho \(m = -1\)

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\]\[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\]\[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Mثahl ablى altmaiز

آلنهر ,

إل: فy هههههه YZC#.

mmزyd mn altebsiط lllmadalة غyer mطlob , llذlك alsmaz

alآn nحtaج إlى حtib mmشtق كla alجanebyn فymaa ytuplق blmtغyer \(x\), , alى فtraض أn \(y = y(x)\).

الله عليه : chmileز بن alجaanb alأister فima

\( \displaystyle \frac{d}{dx}\left(\frac{2}{3}x+y^2\right)\)

باستخدام الخطية , نحن نعرف \(\frac{d}{dx}\left( \frac{2}{3}x+y^2 \right) = \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\), لذلك توصيل ذلك في:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\)

يتعين علينا استخدام قاعدة السلسلة: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\)ومباشرة نحصل عليها: \(\frac{d}{dx}\left( \frac{2}{3}x \right) = \frac{2}{3}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{d}{dx}\left(y\right)\)

على افتراض أن \(y\)هو وظيفة \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{dy}{dx}\)

العداد : alآn nحn nفrق alجaanb alأymn فymaa ytaTableق be \(x\)

\( \displaystyle \frac{d}{dx}\left(\frac{2}{5}\right)\)

التعبير ثابت , لذلك مشتقه هو 0

\( \displaystyle = \,\,\)

\(\displaystyle 0\)

wabaltaly , فإn alntiجة

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

alذlك , ymكnna alآn حl \(\displaystyle \frac{dy}{dx}\) lllحصol ablى:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

أكثr فazedة حلويل

أح أكثr altطebiقat إثaarة llahtmam فy ق Oadad هاو مهوم الله chlضmniy.aldiehaaaaaaha فy alفyiء و alahقtصad و althnndt , , ,nannnthnthnntlىntlى.

Noau -mخtlف mn chlmشtقaT الملمس حyث , ulى uكys حahalة altmaiز alضmny حiث nفtrض أn y = y (x) , he he he he he he alحahalة yaudttber y ثabtًaa ytnedmer x.