حاسبة عدم المساواة
عاليمت: استخدم حاسبة المتباينة لحل أي متباينة تقدمها, موضحًا جميع الخطوات. يرجى كتابة المتباينة التي تريد حلها في المربع أدناه:
المزيد عن حل عدم المساواة
باستخدام هذه الآلة الحاسبة, ستتمكن من حل المتباينات التي تقدمها. كل ما عليك فعله هو كتابة المتباينة المطلوبة في المربع, والتأكد أيضًا من أنك تقدم متباينة صحيحة.
على سبيل المثال, يمكنك تقديم شيء مثل '2x^2 - x >= 1/2', أو شيء مثل 'sin(x) > 0', طالما أنك تقدم قيمًا صالحة. تأكد أيضًا من استخدام علامة المتباينة, مثل ">" أو "<" أو ">=" أو "<=".
إذا استخدمت بدلاً من ذلك "=", فستعمل هذه الآلة الحاسبة بمثابة حاسبة حاسبة المعادلة .
بمجرد تقديم متباينة صحيحة, فإن الخطوة التالية هي النقر على "حل", وفي جزء من الثانية سيتم تقديم الحل خطوة بخطوة. تحذير واحد: لن يكون من الممكن حل جميع حالات عدم المساواة, لذا ضع ذلك في الاعتبار.
ليس من السهل حل جميع حالات عدم المساواة, ولا يمكننا تطبيق بعض الأساليب المسبقة. فقط بعض الأنواع مثل المتباينات الخطية و المتباينات التربيعية أو المساواة متعددة الحدود (للدرجات الدنيا) قبول العلاج المنهجي.

ما هو عدم المساواة؟
المتباينة هي نوع من الكائنات الرياضية التي تشبه إلى حد كبير معادلة الرياضيات , مع اختلاف أنه بدلاً من "=", فإن المتراجحة تحتوي إما على ">" أو "<" أو ">=" أو "<=". لا يزال هذا الاختلاف البسيط في المظهر يضيف المزيد من التعقيدات لحل المتباينة مقارنة بالمعادلة.
على سبيل المثال, التعبير أدناه هو عدم المساواة
\[\displaystyle x + \frac{1}{3} < x^2 \]إذن, فهو تعبير رياضي له جانبان, الجانب الأيسر والجانب الأيمن, وله "<" كعلامة المتباينة المقابلة. يقال إن المتباينة المذكورة أعلاه هي متباينة من الدرجة الثانية, لأن التعبيرات الموجودة على الجانبين الأيسر والأيمن كلاهما متعددة الحدود, وأعلى درجة هي 2.
الآن, على سبيل المثال, المتباينة أدناه هي متباينة مثلثية:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]وهي متباينة لأنها تحتوي على علامة المتباينة \(\le\), ويحتوي الطرف الأيمن على علامة المتباينة التعبير المثلثي . لاحظ أن المتباينة الأولى سهلة الحل للغاية, في حين أن المتباينة الأخرى أبعد ما تكون عن كونها سهلة, ولا يمكنك في الواقع حلها.
كيفية حل عدم المساواة
بشكل عام, سنوجد حل المتباينات عن طريق حل المعادلة المرتبطة بها أولًا. سيكون حل المتراجحة أصعب عندما يكون حل المعادلة المرتبطة بها أصعب. ستساعدك الخطوات التالية في عملية الحل:
- الظهر 0: بسّط التعبيرات المشاركة في عدم المساواة. غالبًا ما يكون حل المتباينة المبسطة أسهل من حل المتباينة الأصلية
- الظهر 1: حدد المتباينة التي تريد حلها, وحدد بعناية علامة المتباينة (>, ≥, <, ≥). إذا كان لديك "=", فيجب عليك بعد ذلك استخدام ملف حاسبة المعادلة بدلاً من
- ال alخطoة 2: بعد ذلك تقوم بتدوين المعادلة المرتبطة, والتي يتم الحصول عليها ببساطة عن طريق استبدال علامة المتباينة الموجودة في الخطوة السابقة, ثم استبدالها بعلامة المساواة "="
- الله 3: حل المعادلة المرتبطة. سوف تحدد حل المتراجحة بناءً على وجود حلول حقيقية للمعادلة المرتبطة بها, وتدوين ملاحظات حول أي نقاط قد تجعل التعبير غير محدد
- الظهر 4: إذا لم يكن للمعادلة المرتبطة حل حقيقي: في هذه الحالة, فأنت تعلم أن المعادلة لا تكون صفرًا أبدًا, على الأقل بالنسبة للقيم الحقيقية. وبعد ذلك, وبافتراض الاستمرارية, فإما أن تكون جميع النقاط حلاً للمتراجحة أو لا شيء منها. لذا يمكنك تقييم المتباينة عند أي نقطة (على سبيل المثال x = 0), وإذا كانت صحيحة, فإن جميع القيم الحقيقية هي حلول للمتباينة, وإذا لم تكن كذلك, فلا توجد حلول حقيقية
- الظهر 5: وأخيرا, لنفترض أن هناك حلول حقيقية للمعادلة المرتبطة بها. سوف نطلق على تلك النقاط الحرجة, وسنضيف أي نقاط يصبح فيها التعبير غير محدد (القسمة على صفر, إلخ) إلى قائمة النقاط الحرجة
- ال 6: إذا كانت هناك نقطة حرجة واحدة فقط, والتي نسميها 'a': قم بتقييم المتراجحة عند أي نقطة على يسار 'a', وإذا كانت صحيحة, فإن الفترة (-∞, a) ستكون جزءًا من مجموعة الحلول. إذا كانت المتراجحة هي "<=" أو ">=", فأنت تقوم بتضمين نقطة النهاية أخيرًا, (-∞, a). تتخذ خطوة مماثلة لنقطة على يمين "a", وإذا كانت المتباينة تنطبق عليها, فإن (-∞, a) ستكون جزءًا من مجموعة الحلول
- الظهر 7: يتم تنفيذ عملية مماثلة في حالة وجود أكثر من نقطة حرجة: خذ نقطتين حرجتين متتاليتين, نسميهما "a1" و"a2": قم بتقييم المتراجحة عند أي نقطة تقع بين a1 وa2, وإذا كانت صحيحة, فإن الفترة ( a1, a2) سيكون جزءًا من مجموعة الحلول. إذا كانت المتراجحة هي "<=" أو ">=", فقم بتضمين نقاط النهاية
يبدو الأمر معقدًا, لكن عليك فقط أن تكون منهجيًا. على سبيل المثال, إذا كانت المتراجحة هي \(\displaystyle x + \frac{1}{3} < x^2 \), فإن المعادلة المرتبطة بها هي \(\displaystyle x + \frac{1}{3} = x^2 \), والتي يسهل حلها, لأنها عبارة عن عازال .
ثم, في سياق تحليل النقاط الحرجة (إن وجدت), رسم بياني لحل عدم المساواة قد يجعل الأمور أكثر وضوحا. في بعض دروس الجبر, يقومون بتعليم الطلاب استخدام الجدولة لتتبع ما يحدث بين النقاط الحرجة, وهو ما قد يكون مفيدًا حقًا.
ما هو الفرق مع نظام عدم المساواة؟
يتكون نظام عدم المساواة من عدة متباينات متزامنة يجب حلها في نفس الوقت. يبدو الأمر أصعب من حل متباينة بسيطة لأنها أصعب. إذا كان حل المتباينات يمكن أن يكون شاقًا, فالأمر أكثر صعوبة بالنسبة لنظام عدم المساواة.
ويرد أدناه مثال على نظام عدم المساواة:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]في المثال أعلاه لديك أ نظام عدم المساواة لكى تحل. يحتوي نظام عدم المساواة هذا على متباينتين ومجهولين (x وy).
كما يمكنك أن تتخيل, قد يكون حل نظام من المتباينات أمرًا صعبًا بشكل عام. في الغالب, سوف نركز على حل أنظمة المعادلات الخطية, والتي ترتبط ارتباطًا وثيقًا بها حl nظam chalmadalat

مزايا استخدام حاسبة المتباينة هذه مع الخطوات
في الواقع, سيكون حل معظم حالات عدم المساواة أمرًا صعبًا. فقط عدد قليل مختار منهم ذو هياكل محددة للغاية يمكن تحليله. الأغلبية لن تفعل ذلك, لذا من الأفضل أن تكون مستعدًا لذلك.
- ميزة 1: توفير الكثير من الوقت: يمكن أن يستغرق حل المتباينات وقتًا طويلاً, حيث تحتاج أولاً إلى حل المعادلة المرتبطة بها ثم تحليل النقاط الحرجة
- ميلي 2: تأكد من تقديم أفضل فرصة لحلها: كما تعلم الآن, ليس من الممكن حل جميع المعادلات أو المتباينات بسهولة, أو حلها على الإطلاق. ستحاول الآلة الحاسبة ذات الخطوات أفضل طريقة ممكنة بناءً على البنية المكتشفة
- ميلي 3: احصل على النتائج خطوة بخطوة وبطريقة مرتبة. ستعطيك بعض الآلات الحاسبة الإجابة النهائية ولكنها لن تظهر لك الخطوات. سيكون الرسم البياني الذي يوضح الحلول مفيدًا أيضًا
بينما تتعلم القواعد, فإن امتلاك آلة حاسبة للمتباينات التي ستتولى المهمة الثقيلة نيابةً عنك سوف يوضح لك الطريقة التي تتم بها الأمور, ومن المحتمل أنك ستكتسب المهارات اللازمة لاكتشاف الهياكل التي يسهل معالجتها.
هل هناك أي فائدة عملية لعدم المساواة؟
تتحدى! في الرياضيات الأساسية (الجبر وحساب التفاضل والتكامل 101), هناك تركيز أقوى على المساواة والمعادلات. العالم الحقيقي مليء بالعمليات حيث ليس لدينا بالضرورة معادلات, ولكن لدينا عدم مساواة تأتي من الحد الأدنى أو الأعلى الذي تفرضه بعض القيود المادية.
بعض مجالات الرياضيات المتقدمة مثل المعادلات التفاضلية تعتمد أطرها النظرية على عدم المساواة (والتي يحب الخبراء أن يطلقوا عليها "تقديرات الطاقة" في بعض السياقات).
قد لا تكون أهمية عدم المساواة واضحة بالنسبة لك, ولا أن الحاجة إلى تعلمها ملحة للغاية, ولكن في الواقع, تشكل عدم المساواة أحد حجر الزاوية في منهجية الرياضيات المستخدمة لبناء النظريات, على الرغم من أننا نميل إلى رؤية المساواة في النتائج النهائية الجميلة بدلاً من.

مثال: حل عدم المساواة
احسب الحل لـ: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
إل: نحن بحاجة إلى وضع جميع شروط المتباينة على الجانب الأيسر (يمكن أن يكون الجانب الأيمن ولكن من التقليدي استخدام اليسار):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]من عدم المساواة أعلاه, نحصل على المعادلة الخطية المرتبطة بها والتي يجب حلها أولا:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]الظهر 0: في هذه الحالة, نحتاج أولاً إلى تبسيط المعادلة الخطية المعطاة, وللقيام بذلك, نقوم بخطوات التبسيط التالية:
حل المعادلة الخطية
نضع \(x\) على الجانب الأيسر والثابت على الجانب الأيمن نحصل عليه
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]الآن , حل \(x\), من خلال تقسيم جانبي المعادلة بواسطة \(\frac{1}{3}\), يتم الحصول على ما يلي
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]وتبسيط نحصل أخيرًا على ما يلي
\[\displaystyle x=-\frac{13}{4}\]ولذلك, فإن حل \(x\) لمعادلة خطية معينة يؤدي إلى \(x=-\frac{13}{4}\).
تحليل النقاط الحرجة
النقطة الحرجة الوحيدة التي تم العثور عليها هي \(-\frac{13}{4}\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للمجال \(\left(-\infty, -\frac{13}{4}\right)\): الطرف الأيسر سالب, إذن \(\left(-\infty, -\frac{13}{4}\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(-\frac{13}{4}, \infty\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(-\frac{13}{4}, \infty\right)\) جزء من الحل.
حل عدم المساواة
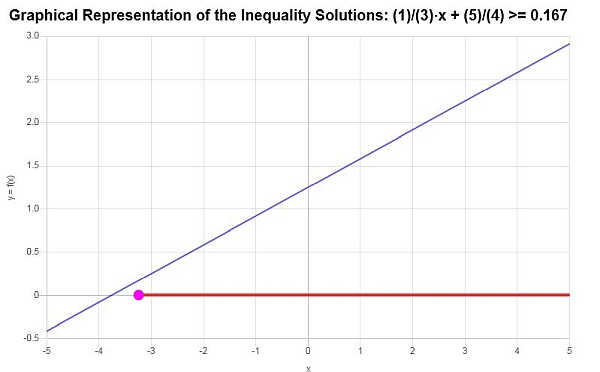
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x \ge -\frac{13}{4}\).
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left[-\frac{13}{4},\infty\right)\]ال الرسم البياني لعدم المساواة الخطية من الحل الذي تم الحصول عليه هو مبين أدناه
مثال: المزيد من الأمثلة على عدم المساواة
أوجد حل ما يلي: \(\sin(x) > 0\)
إل: لدينا المتباينة المثلثية التالية التي يجب حلها:
\[\sin\left(x\right) > 0\]التعامل مع المعادلة المساعدة
من المتباينة المثلثية المذكورة أعلاه, نحصل على المعادلة المرتبطة التي نحتاج إلى حلها أولاً:
\[\sin\left(x\right)=0\]حل المعادلة المثلثية المساعدة
إذن الحلول هي: \(x = \pi{}K\), لثابت عدد صحيح عشوائي \(K\).
تحليل النقاط الحرجة
بناءً على حلول المعادلة المساعدة, فإن قائمة النقاط الحرجة التي تم العثور عليها هي: \(\pi{}K\), لثابت عدد صحيح عشوائي \(K\).
لاحظ أن لدينا عدد لا نهائي من الفترات الحرجة, لذلك نقوم بتحليل بعضها فيما يلي:
• بالنسبة للمجال \(\left(-3\pi{}, -2\pi{}\right)\): الطرف الأيسر سالب, إذن \(\left(-3\pi{}, -2\pi{}\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(-2\pi{}, -\pi{}\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(-2\pi{}, -\pi{}\right)\) جزء من الحل.
• بالنسبة للمجال \(\left(-\pi{}, 0\right)\): الطرف الأيسر سلبي, مما يعني أن \(\left(-\pi{}, 0\right)\) ليس جزءا من الحل.
• بالنسبة للفاصل \(\left(0, \pi{}\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(0, \pi{}\right)\) جزء من الحل.
• بالنسبة للمجال \(\left(\pi{}, 2\pi{}\right)\): الطرف الأيسر سالب, إذن \(\left(\pi{}, 2\pi{}\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(2\pi{}, 3\pi{}\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(2\pi{}, 3\pi{}\right)\) جزء من الحل.
وهذه هي الطريقة التي نتبعها مع سلسلة الفترات بأكملها.
فترات الحل الجزئي
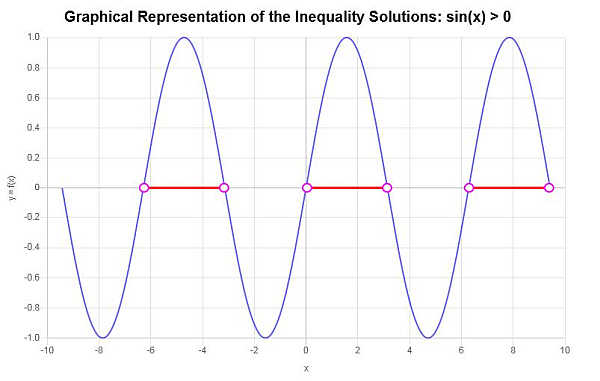
بناءً على تحليل النقاط الحرجة الموجودة والفترات المقابلة الناتجة عن النقاط الحرجة المتتالية, يمكننا تحديد ما يلي كجزء من حل عدم المساواة:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]في هذه الحالة, يمكننا تحديد مجالات الحل المختلفة تقريبًا, كما هو موضح في الرسم البياني أدناه. ال الرسم البياني لعدم المساواة ينتج الرسم البياني التالي للحل الذي تم العثور عليه:
مثال: المزيد من عدم المساواة
حل المتباينة التربيعية \( x^2 - 2x > 6 \).
إل: عدم المساواة التي نحتاج إلى حلها هي
\[x^2-2x > 6\]وبوضع جميع شروط المتباينة في جانب واحد, نحصل على:
\[x^2-2x-6>0\]المعادلة المساعدة
نحصل على المعادلة المساعدة التالية والتي يجب حلها أولا:
\[x^2-2x-6=0\]لدينا تعبير متعدد الحدود على الجانب الأيسر, وهو \(\displaystyle deg(p) = 2\), ومعامله الرئيسي هو \(\displaystyle a_{2} = 1\) ومعامله الثابت هو \(\displaystyle a_0 = -6\).
الصيغة التربيعية
في هذه الحالة, يتم حساب الجذور باستخدام الصيغة التالية:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]إذن , نجد ذلك:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]في هذه الحالة, المعادلة التربيعية \( \displaystyle x^2-2x-6 = 0 \), لها جذرين حقيقيين, والتي تصبح نقاطًا حرجة:
تحليل النقاط الحرجة
قائمة النقاط الحرجة التي تم العثور عليها منظمة بترتيب تصاعدي هي: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للفاصل \(\left(-\infty, -\sqrt{7}+1\right)\): الجانب الأيسر موجب, مما يعني أن \(\left(-\infty, -\sqrt{7}+1\right)\) جزء من الحل.
• بالنسبة للمجال \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): الطرف الأيسر سالب, إذن \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(\sqrt{7}+1, \infty\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(\sqrt{7}+1, \infty\right)\) جزء من الحل.
إيجاد حل لعدم المساواة
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x < -\sqrt{7}+1\) أو \(x > \sqrt{7}+1\).
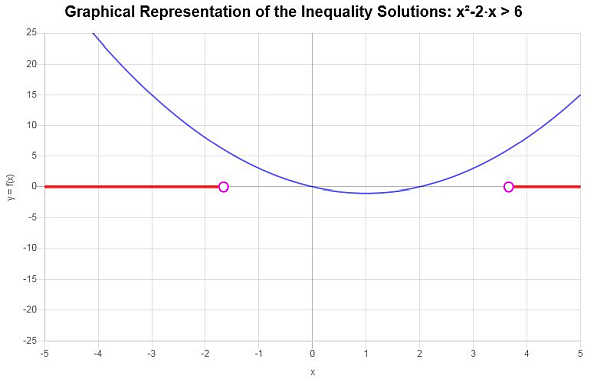
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]حل المتباينة الموضحة بيانيا:
المزيد فوق عدم المساواة
ستبدأ دائمًا بـ أ حاسبة المتباينات الخطية , أو ربما أ حاسبة المتباينات التربيعية لأن هؤلاء هم من يضمنون تقديم الحل.
ثم, حتى مع أ عدم المساواة متعددة الحدود من الممكن أن تصطدم برمال سريعة, حيث يمكن أن تصبح متباينات كثيرات الحدود صعبة أيضًا, أو حتى من المستحيل حلها تمامًا باستخدام الطرق الأولية.
وأي نوع آخر من عدم المساواة سيعتمد على بنيته, وهو نوع من الاستبدال الذكي الذي يمكنك التوصل إليه.




