المتباينات متعددة الحدود
عاليمت: استخدم حاسبة متباينة كثيرات الحدود لحل أي متباينة متعددة الحدود, موضحًا جميع خطوات العملية. الرجاء كتابة متباينة متعددة الحدود في المربع أدناه.
المزيد عن المتباينات كثيرة الحدود
يمكن أن تساعدك هذه الآلة الحاسبة في حل متباينات كثيرة الحدود, من خلال إظهار جميع خطوات عملية حساب الحل, بالإضافة إلى تزويدك برسم بياني للمتباينة, يصور الحل
يمكن أن تكون المتباينة التي تقدمها شيئًا بسيطًا مثل 'x^2 > 1', أو يمكن أن تكون أكثر تعقيدًا مثل 'x^3 + 3x^2 + 3x + 1 > 0'.
بمجرد توفير متباينة متعددة الحدود صالحة, يرجى المتابعة والنقر على زر "احسب", للحصول على الحل وجميع الخطوات الموضحة.
يرجى العلم أنه ليست كل كثيرات الحدود التي تقدمها سوف تصلح للحلول الدقيقة. كلما انخفضت درجة كثيرة الحدود, زاد احتمال العثور على حل دقيق للمتباينة.

ما هي عدم المساواة كثيرة الحدود
المتباينة كثيرة الحدود هي ببساطة نوع من المتباينة التي تكون فيها التعبيرات المعنية متعددة الحدود, ولا يعد أي من مصطلحاتها تعبيرًا غير متعدد الحدود. على سبيل المثال
\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]هي عدم المساواة كثيرة الحدود, في حين
\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]ليس, بسبب وجود المصطلح \(\sin x\), وهو ليس متعدد الحدود. حل عدم المساواة بشكل عام هي عملية صعبة بشكل عام, ولكن بالنسبة للكثيرات الحدود, لدينا خطة عمل واضحة.
كيف يمكنك حل عدم المساواة كثير الحدود
- الظهر 1: تأكد من أن جميع المصطلحات متعددة الحدود. إذا لم يكن الأمر كذلك, فقد لا يتم تطبيق الطرق المحددة المستخدمة في كثيرات الحدود
- ال alخطoة 2: ضع كل شيء على جانب واحد, واترك الصفر على الجانب الآخر
- الله 3: استبدال علامة المتباينة بـ "=", حل المعادلة المرتبطة (وهذا يتضمن إيجاد أصفار كثيرة الحدود)
- الظهر 4: اجمع كل النقاط الحرجة للمتباينة, والتي في هذه الحالة هي الأصفار الحقيقية للقيمة المساعدة معادلة كثيرة الحدود (لا تأخذ في الاعتبار الجذور المعقدة في هذه الحالة)
- الظهر 5: إذا لم تكن هناك نقاط حرجة, فهذا يعني أن التعبير لا يغير الإشارة, وبالتالي فإن الخط الحقيقي بأكمله سيكون حلاً, وإلا فلا يوجد حل. للتحقق, اختر أي نقطة ومعرفة ما إذا كانت تحقق المتراجحة, وإذا كانت تحققها, فإن الخط الحقيقي بأكمله هو الحل, وإذا لم يكن كذلك, فلا يوجد حل
- ال 6: إذا كانت هناك نقاط حرجة, فقم بإنشاء فواصل زمنية بنقاط حرجة متتالية (باستخدام -∞ كنقطة حرجة للبدء, و∞ كنقطة حرجة للنهاية)
- الظهر 7: تحقق من كل فترة من هذه الفترات, ولاحظ ما إذا كانت هناك نقطة داخلها تحقق المتراجحة. إذا كان الأمر كذلك, فإن الفاصل الزمني جزء من الحل, وإذا لم يكن كذلك, فإن الفاصل الزمني ليس جزءًا من الحل.
الفكرة الأساسية هنا هي أن النقاط الحرجة والفترات التي نشتقها منها هي فترات لا يغير التعبير علاماتها, لذا إما أن تكون الفترة بأكملها حلاً, أو عدم وجود نقطة في الفترة هي جزء من الحل.
الأصفار كثيرة الحدود والنقاط الحرجة
أحد الأسباب التي تجعل حل متباينات كثيرات الحدود أمرًا ممكنًا هو أنه من السهل نسبيًا تحليل تعبيرات كثيرات الحدود بحثًا عن نقاط حرجة, بصرف النظر عن حقيقة أن كثيرات الحدود هي تعبيرات مستمرة.
سيكون هناك عدم المساواة مثل
\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]حيث سيكون من الصعب جدًا العثور على النقاط الحرجة. المتباينات الخطية من الأسهل العثور على النقاط الحرجة, ولكن هذا كل ما في الأمر. إن أي تفاوت عام سوف ينطوي على تعقيداته الخاصة.

تطبيقات كثيرات الحدود في الحياة الحقيقية
هناك الكثير من تطبيقات كثيرات الحدود. على سبيل المثال, في الفيزياء عندما تدرس علم الحركة, هناك بعض التعبيرات متعددة الحدود المثيرة للاهتمام المستمدة من قوانين نيوتن. يمكن لهذه التعبيرات تحديد شروط موضع الجسم, مما قد يؤدي إلى عدم مساواة متعددة الحدود لتحديد الأوقات التي يكون فيها الجسم فوق ارتفاع معين, وهو ما قد يكون حاسمًا في المقذوفات, على سبيل المثال.
أيضًا, عند دراسة المعادلات التفاضلية, يمكنك العثور على مصطلحات قلابة في المعادلة التي تعتمد على قوة, ولها بنية متعددة الحدود, والتي يمكنك استخدام بعض المتباينات المتقدمة فيها, مثل متباينات جرونوال.

مثال: حل المتباينات كثيرة الحدود
حل: \(x^2 - x > \frac{1}{2}\)
إل: نحتاج أولاً إلى حل المعادلة التربيعية التالية \(\displaystyle x^2-x-\frac{1}{2}=0\):
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]إذن , نجد ذلك:
\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]تحليل النقاط الحرجة
قائمة النقاط الحرجة التي تم العثور عليها منظمة بترتيب تصاعدي هي: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للفاصل \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): الطرف الأيسر موجب, إذن \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) جزء من الحل.
• بالنسبة للمجال \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): الطرف الأيسر سلبي, مما يعني أن \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) ليس جزءا من الحل.
• بالنسبة للفاصل \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): الطرف الأيسر موجب, مما يعني أن \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) جزء من الحل.
حل عدم المساواة
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) أو \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]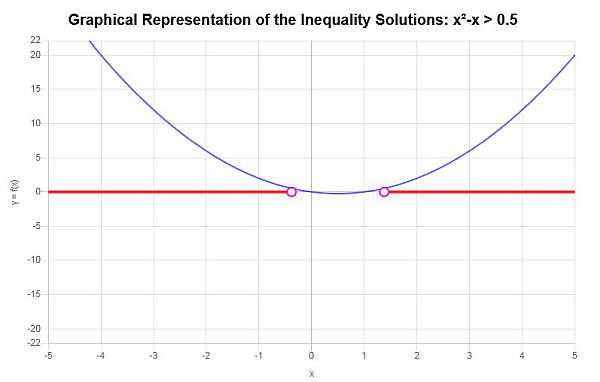
الذي يختتم الحساب.
مثال: متعدد الحدود بدرجة أعلى
حل المتباينة التالية: \(x^3 - x > 1\)
حل:
من أجل حل \(x^3-x > 1\) نضع كل شيء أولاً على جانب واحد:
\[x^3-x-1> 0\]الآن, من هذا نحصل على المعادلة المرتبطة التي يجب حلها أولاً, وهي \(x^3-x-1=0\). لاحظ أن الدرجة هي \(\displaystyle deg(p) = 3\) ومعاملها الرئيسي هو \(\displaystyle a_{3} = 1\) ومعاملها الثابت هو \(\displaystyle a_0 = -1\).
محاولة الجذور العقلانية
سنحاول إيجاد جذور كسرية بسيطة أولًا باستخدام نظرية الصفر.
المهمة التالية هي العثور على الأعداد الصحيحة التي تقسم المعامل الرئيسي \(a_{3}\) والمعامل الثابت \(a_0\), والتي سيتم استخدامها لبناء مرشحينا ليكونوا أصفارًا في المعادلة كثيرة الحدود.
▹ مقسمات \(a_{3} = 1\) هي: \(\pm 1\).
▹ مقسمات \(a_0 = -1\) هي: \(\pm 1\).
لذلك, بقسمة كل مقسم للمعامل الثابت \(a_0 = -1\) على كل مقسم للمعامل الرئيسي \(a_{3} = 1\), نجد القائمة التالية من المرشحين لتكون جذور:
\[\pm \frac{ 1}{ 1}\]الآن , يجب اختبار جميع المرشحين لمعرفة ما إذا كانوا حلًا.يتم الحصول على ما يلي من اختبار كل مرشح:
\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:& & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:& & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]ولكن نظرًا لأننا لم نعثر على أي جذور عقلانية عن طريق التفتيش , لا يمكننا الاستمرار في العوامل باستخدام الطرق الابتدائية , وبالتالي تتوقف العملية هنا.
خياري : هذه كثيرة الحدود من الدرجة \(3\), والتي يوجد لها إجمالي \(3\) الجذور, حتى لو كان بعضها معقدًا, ولكن في هذه الحالة تم العثور على حلول أقل من \(3\) باستخدام الطرق الأولية.
وباستخدام طرق المعادلات التكعيبية المتقدمة, نجد أن مجموعة الحلول الكاملة هي:
\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
تحليل النقاط الحرجة
النقطة الحرجة الوحيدة التي تم العثور عليها هي \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).
وبناءً على ذلك, نحتاج إلى تحليل الفترات التالية:
• بالنسبة للمجال \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): الطرف الأيسر سالب, إذن \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) ليس جزءًا من الحل.
• بالنسبة للفاصل \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): الجانب الأيسر موجب, مما يعني أن \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) جزء من الحل.
حل عدم المساواة
وبناء على المتباينة المقدمة, وتحليل النقاط الحرجة نجد أن حل المتراجحة هو: \(x > 1.3247180451128\).
باستخدام تدوين الفاصل الزمني, يتم كتابة الحل على النحو التالي:
\[\left(1.3247180451128,\infty\right)\]بيانياً:
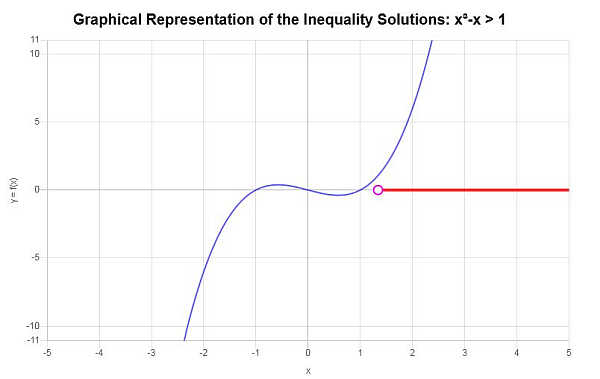
المزيد من الآلات الحاسبة لعدم المساواة
حل عدم المساواة (منعت من إيجاد حلول للمعادلات ) هي إحدى العمليات الأكثر شيوعًا في الرياضيات, في جميع المجالات.
عادة ما تكون عملية حل المتباينات شاقة, وبشكل عام لا توجد قاعدة لحلها. حل المتباينات كثيرة الحدود هي واحدة من الاستثناءات القليلة, التي يمكننا من خلالها اتباع مجموعة من الخطوات للعثور على الحلول, ولكن مع ذلك, لا يزال من الممكن أن نفشل, لأن متعددات الحدود ذات الدرجة الأعلى يصعب التعامل معها. في الواقع, فإنه من المستحيل حقا أن العثور على جذور متعددة الحدود فوق الدرجة الخامسة باستخدام القاعدة العامة (نظرية هابيل).







