衍生品计算器
指示: 使用这个导数计算器来寻找你提供的函数的导数,显示这个过程的所有步骤。请在下面的方框中输入你想计算的函数的导数。
衍生品计算器
这个导数计算器将带你完成所有的步骤和规则,用来寻找一个给定函数的导数。你必须输入一个函数,如3x + sin(x^2),或者你实际上可以在前面加上整个函数定义,如f(x) = 3x^ 2 + 2tan(x^3)。
请注意,这可以被称为第一导数计算器,与导数计算器相同。一阶导数和导数代表的是同一件事,而 "一 "的部分通常被去掉。
所提供的函数可以完全简化或不简化,这并不重要,因为如果有必要,计算器会在计算其导数之前首先简化函数。
一旦一个 有效功能 已经提供,你只需要点击 "计算",等待几秒钟,所有的计算步骤就会呈现在你面前。
微分是微积分中使用的主要工具(与积分一起),它是在更高级的数学中广泛使用的一个重要操作。一些非常常见的应用包括 切线计算 ,最大和最小值以及更多。
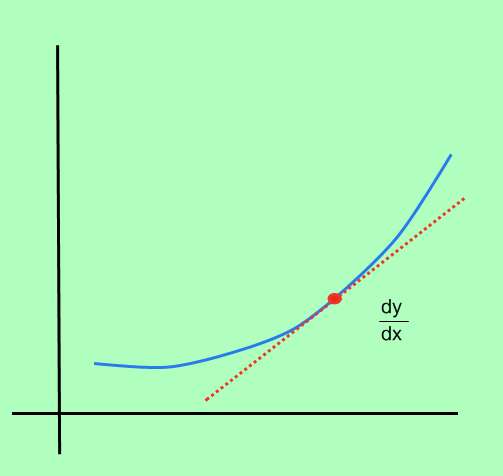
如何计算一个函数的导数?
计算一个函数的导数的过程被称为 差异化 ,它包括确定点的即时变化率,在函数域中的每一点。
什么是一个函数的即时变化率?好吧,让我们从以下的定义开始 变化率 :考虑一个函数\(f\),并假设我们有两个点,\(x_0\)和\(x_1\)。在\(x_0\)点,函数为\(f(x_0)\),在\(x_1\)点,函数的值为\(f(x_1)\)。
那么,f的变化被定义为\(\Delta y = f(x_1) - f(x_0)\)(也被称为y的变化)。另外,x的变化被定义为\(\Delta x = x_1 - x_0)\)。简单地说,\(\Delta x\)是x的变化,而\(\Delta y\)是函数值的变化,由于x的变化。
在图形上。
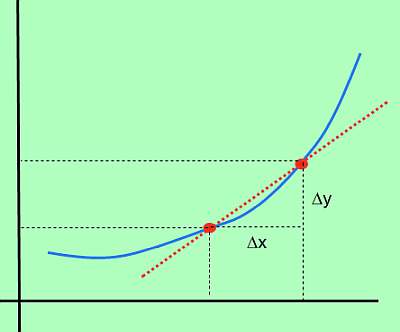
衍生公式
因此,如果\(\Delta x\)代表x的变化,而\(\Delta y\)代表函数值的变化,由于x的变化,相应的 变化率 是。
\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]那么,瞬间的变化率会是多少呢?这就相当于分析如果\(\Delta x\)变得非常小会发生什么。人们期望\(\Delta y\)也会变小,但是\(\Delta y\)和\(\Delta x\)之间的变化率会发生什么?
因此,在这种情况下,即时变化率被定义为
\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]所以,通俗地说,我们把\(x_0\)固定下来,然后计算越来越接近\(x_0\)的\(x_1\)值的变化率。利用这个即时变化率的概念,我们可以给出在\(x_0\)点的导数的下列公式。
\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]如果上述极限存在,我们说函数f在\(x_0\)是可微的。另外,我们将说一个函数在集合A处是可微的,如果该函数在该集合的每一点都是可微的。
使用导数公式的步骤
- 步骤1: 明确指出你要微分的函数f
- 第2步: 确保你尽可能地简化f,否则找到所需的极限可能会有不必要的困难
- 第3步: 决定你是用一个通用的点x0工作,还是给x0一个特定的数字点
- 第4步: 根据该函数的定义,使用公式\(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \)。也就是说,将x0和x1的值插入f中,看看这个公式在代数上是怎样的
- 第5步: 在采取限制措施之前,尽可能地简化程序。
- 第6步。 有时,设置x1=x0+h,然后计算h收敛到0时的极限,会更容易。
请注意,步骤6是一些人喜欢的默认步骤。事实上,出于简化的目的,另一个看起来更容易的导数公式是。
\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]这是你可能在课本上找到的公式,而不是另一个。
衍生品规则
用这个公式计算导数似乎是一件很麻烦的事情。事实上,如果我们决定用导数公式计算每个微分过程,这可能是一个费力的过程。
幸运的是,有一些函数(即 多项式 , 三角函数 ),我们准确地知道它们的导数是什么。
在此基础上,我们有 差异化规则 允许我们找到一个函数的导数,该函数是一个 复合功能 和/或初级函数的组合(对于这些函数,我们知道它们的导数),以初级导数为例。
计算导数的步骤是什么?
- 步骤1: 确定你要微分的函数f。在计算其导数之前,尽可能地简化。
- 第2步: 确定你是否需要使用导数公式
- 第3步: 如果你必须使用导数公式,请使用\(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \),或者你可以使用\(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \),如果它看起来更容易接近。
- 第4步: 如果你不需要使用导数公式,你可以使用主要的微分规则。直线性。 产品规则 , 商数规则 和 链条规则 ,这将有助于你将导数的计算减少到使用基本的已知导数
通常情况下,你所尝试的功能是 求导数 for不是一个简单的函数,但它是几个简单函数的基本组合。例如,函数
\[f(x) = x + \cos(x) + \sin(x)\]本身不是一个基本的函数,但它是 复合功能 的三个基本函数,\(x\),\(\sin x\)和\(\cos x\)。
衍生品的应用
人们可能会认为 "好吧,导数涉及极限,那是超级理论,所以它一定没有太多应用",但你会完全错了。导数的神奇之处在于,它们本质上是关于函数的变化率,可以代表不同类型的过程。
这就是为什么差异化允许研究变化的过程,以及如何比较变化的变量,这具有广泛的适用性。
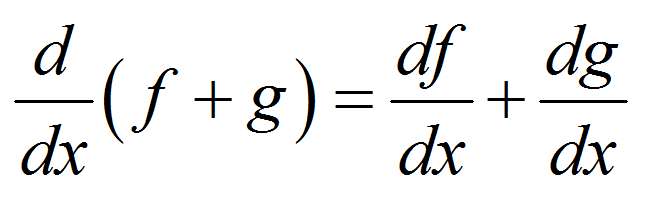
例子。计算导数
计算\(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)相对于x的导数
解决方案: 已经提供了以下函数:#\(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\),我们需要计算其导数。
最初的步骤。 在这种情况下,我们首先需要简化给定的函数\(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \),为了做到这一点,我们进行以下简化步骤:
简化函数后,我们可以进行导数的计算。
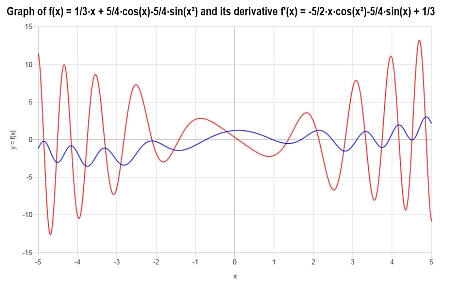
以下是\(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\)在\([-5, 5]\)区间的图:
例子。对一个函数进行微分
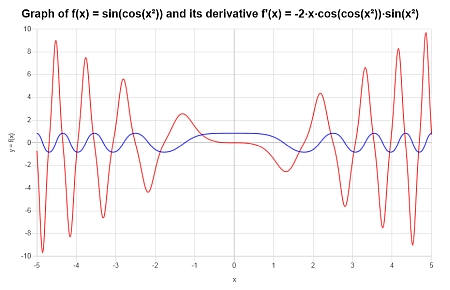
计算...的导数:\(f(x) = \sin(\cos(x^2))\),并提供\(f(x)\)和\(f'(x)\)的图形。
解决方案: 现在我们有了\(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\)。
该函数已经简化,所以我们可以直接计算其导数。通过使用这个导数卡,我们得到:
因此,我们可以得到以下函数在区间\([-5, 5]\)的图:
例子。衍生品计算器
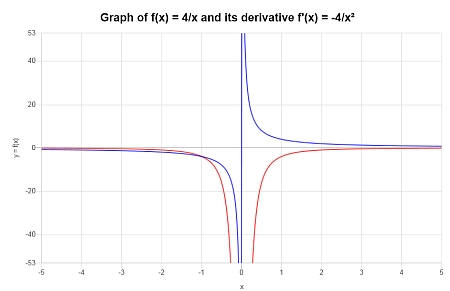
找到\( f(x) = \displaystyle \frac{4}{x}\)的导数。它是否在任何地方都定义良好?绘制图表。
解决方案: 所提供的需要导数的函数是\(\displaystyle f(x)=\frac{4}{x}\)。
不需要进一步简化,所以我们可以直接计算其导数。
在图形上。
关于导数和函数的更多信息
这个 带步骤的导数计算器 将证明对你非常有用,因为它将进行任何给定函数的导数计算,显示该过程的所有步骤,应用适当的 衍生品规则 ,并告诉你什么时候应用以及为什么。
这个计算器也可以被称为 dy dx 计算器 或 微分商计算器 因为这正是它所做的,它计算了dx接近0时dy/dx比率的极限。
函数是数学中极其重要的结构。除了微分之外,你还需要能够 简化一个函数 通常,作为其他更专门的计算的前奏。有一些特殊类型的函数,允许你进行特定的操作,比如你用 多项式运算 .
有趣的是,很多重要的元素,如找到了 "中国 "的坐标。 抛物线的顶点 可以用几何论证的方式巧妙地推导出,可以用微分的方式简单地得到。



