关于链式法则

该计算器将允许您将链式法则应用于您提供的任何复合函数。 A 复合功能 对应于在函数内部计算函数的情况。为了让链式法则计算器工作,您需要提供一个有效的,可微分的复合函数。

一个有效函数的例子是 f(x) = (sin(x))^2,在这里我们有函数 'x^2' 在另一个函数 sin(x) 上计算,形成一个复合函数。

一旦提供了一个有效的,可微分的函数,接下来你要做的就是点击"计算"按钮,这将启动计算,你将看到所有的步骤。

链式法则导数是最常用的微分法则之一。这是因为函数组合是基于基本函数构造新函数的最自然方式之一。

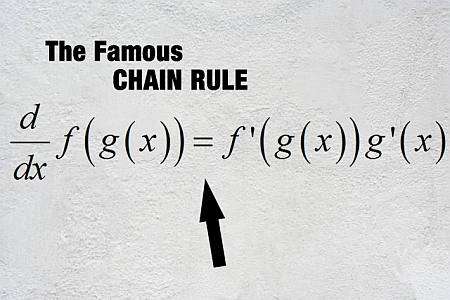
什么是链式法则

简单来说,链式法则允许区分复合函数,这是在其他函数内部求值的函数。所以,假设我们有函数 \(f(x)\) 和 \(g(x)\),并且我们知道如何计算这些函数的导数,它们是 \(f'(x)\) 和 \(g'(x)\)。

然后,有一个 链式规则公式 这允许我们计算复合函数 \(f \circ g\) 的导数,它被定义为 \((f \circ g)(x) = f(g(x))\)：

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

使用链式法则的步骤

• 步骤1： 识别外部函数 f(x) 和内部函数 g(x)
• 第2步： 确保 f(x) 和 g(x) 是有效的可微函数,并计算相应的导数 f'(x) 和 g'(x)
• 第 3 步： 使用公式(f \circ g)'(x) = f'(g(x))g'(x),表示我们在内函数求外函数的导数,乘以导数内部功能

观察上面的步骤如何使用"内部"和"外部"功能的概念。这可能不是一个标准术语,而是一个可以帮助您识别每个函数在使用链式法则时所扮演的角色的想法。

链式法则应用

链式法则确实是寻找衍生品的绝佳工具,而且通常是任何衍生品的关键 导数计算器 ,连同所有其他基本 衍生品规则 .但是链式法则在所谓的 相关利率

为了给出相关率概念的上下文,让我们从一种可能很多人会发现更容易掌握的链式法则的编写形式开始：

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

链式法则的上述形式是说,如果 \(y\) 是 \(z\) 的函数,而 \(z\) 是 \(x\) 的函数,那么最终 \(y\) 是\(x\) 的函数,您可以使用链式法则求 \(y\) 关于 \(x\) 的导数。

您可能已经怀疑,\(y\) 扮演 \(f(x)\)（"外部"函数）的角色,而 \(z\) 扮演 \(g(x)\)（"内部"函数）的角色。

链式法则的上述形式将 y 相对于 x 的变化率与 y 相对于 z 的变化率以及 z 相对于 x 的变化率联系起来,因此称为"相关率"。

这在实践中非常有用。例：圆的半径以每秒2厘米的速度增加,求圆面积的变化率是多少？因此,您可以将圆的半径表示为 t 的函数,反映它以 2 厘米/秒的速度增加的事实,或者,您可以使用链式法则。

所以你称 A 为面积,r 为半径,t 为时间。你需要计算的是\(\displaystyle \frac{dA}{dt}\),所以你直接用链式法则,因为你知道\(A = \pi r^2\),并且r'(t) = 2,那么

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

偏导数链式法则

你能用链式法则吗 部分导数 ？当然,偏微分和正微分一样,只是假设其他变量不变,所以通常的 衍生品规则 申请。

那么,多变量链式法则的理想适用,一次只有一个变量发生变化。

链式规则集成

从某种意义上说,链式法则不适用于衍生工具,而是成为变量替换和更改的宝贵集成工具。

可以将其视为某种反向链式法则。

示例：使用链式法则

计算函数的导数：\(f(x) = \sin(\cos(x)) \)

解决方案： 考虑函数 \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\)。该函数对应于两个函数的组合：sin(x) 和 cos(x),因此链式法则适用于这种情况。

结论是什么 ：我们可以得出结论,我们正在寻找的导数是：

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

这就结束了计算。

链式规则示例

使用链式规则和任何其他派生规则,计算：\(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

解决方案： 在此示例中,我们有函数 \(\displaystyle f(x)=\cos\left(x^2\right)\),它对应于一个复合函数,表明链式法则是开始的右导数规则（计算过程中将需要其他规则）

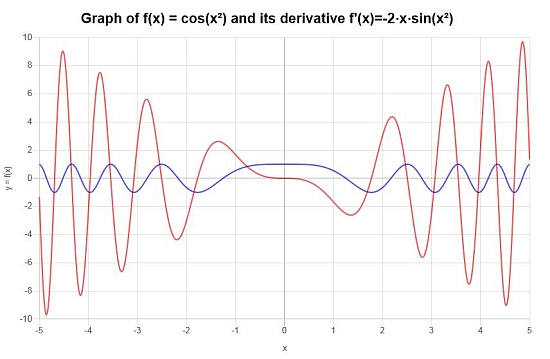
最终导数 ：结论是提供的函数的导数由下式给出：

\[f'(x) = -2x\sin\left(x^2\right)\]

我们可以在区间\([-5, 5]\)上构建如下图形描述：

示例：另一个链式规则计算

使用链式法则计算 \( f(x) = x^2 \sin(x^2)\) 的导数。

解决方案：

已经提供了以下函数。\(\displaystyle f(x)=x^2\sin\left(x^2\right)\),我们需要计算其导数。

该函数已经简化,所以我们可以直接计算其导数。

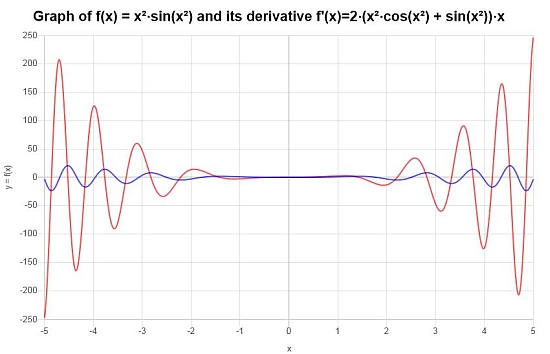
最后的结论是什么 ：最后的结论是,我们要找的导数由下式给出：

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

在图形上我们有：

其他衍生计算器

当然使用 衍生品计算器 在处理相当复杂的功能时会让事情变得更容易。区分的过程通过使用共同的,容易记住的东西而变得更大 衍生品规则 ,包括 产品规则 , 这 商数规则 和 链条规则 .

这些规则将帮助您处理每一个可微分的函数,但是计算和计算的代数过程 简化 不一定容易。