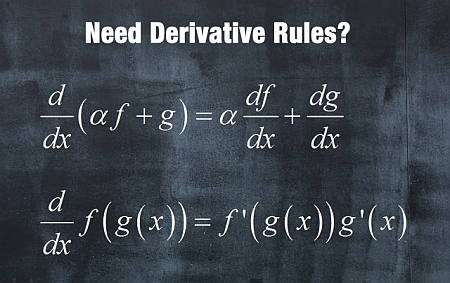求解器微积分

衍生品规则

指示： 使用这个导数计算器寻找你提供的任何函数的导数,使用最常见的导数规则,显示所有的步骤。请在下面的表格框中输入你要应用导数规则的函数。

关于衍生品规则

这个计算器将允许你通过应用所需的基本微分规则来计算你提供的函数的导数,显示这个过程的所有步骤,并注意到每个规则的应用位置。

你只需要提供一个有效的,可微的函数（这意味着它有一个导数）。例如,一个有效的函数可以是f(x)=1/3*x*sin(x),仅举一例。

然后,当你已经输入了你的函数,你只需点击 "计算 "就可以得到所有的微分步骤。

衍生品规则的简单性使得区分的过程被认为是 "容易 "的,这种判断也许是夸张的。

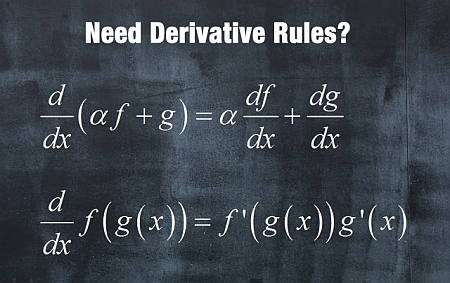
基本衍生品规则

有四个基本的衍生品规则供你学习

线性规则。 对于函数\(f(x)\)和\(g(x)\),以及一个常数\(a\),那么导数是一个线性运算。\((af(x)+g(x))' = af'(x)+g'(x)\)
产品规则 对于函数\(f(x)\)和\(g(x)\),积的导数为\((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)。
商数规则。 对于函数\(f(x)\)和\(g(x)\),商的导数是\(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)。
链条规则 对于函数\(f(x)\)和\(g(x)\),复合函数的导数为\((f(g(x)))' = f'(g(x))g'(x)\)。

这个规则将像一个魅力,将帮助你找到任何基本函数的导数。

如何使用衍生品规则？

步骤1： 确定你要微分的函数f(x),如果需要的话,请进行简化。
第2步： 尝试将函数分解成更小的导数块,使用线性的方式
第 3 步： 根据函数f(x)的结构,使用任何可用的规则（积,商和连锁规则）,并注意你可能需要连续应用许多规则)

通常情况下,你会把几个微分规则结合起来,直到你找到一个基本的函数,你已经知道如何微分。

我可以解决所有的导数吗？

说使用微分规则可以使你解决所有的导数是夸大其词的。你将能够求解大多数导数,当然也包括所有的基本导数,但有些函数的行为不那么直观,可以被定义,尽管它们通常不在基础微积分课程中涉及。

对于哪些基本功能,大部分都会被区分出来,没有问题。

A 乘积规则导数 , 商数规则导数或者链规导数不太可能是孤立的,很可能是由几个需要一起使用的规则组成的序列。

例子。衍生规则

使用基本导数规则,计算以下导数。\(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)<

解决方案：让我们考虑以下需要计算导数的给定函数\(\displaystyle f(x)=x^2\cos\left(x^2\right)\)。

该函数不需要简化,所以我们可以直接计算其导数。

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

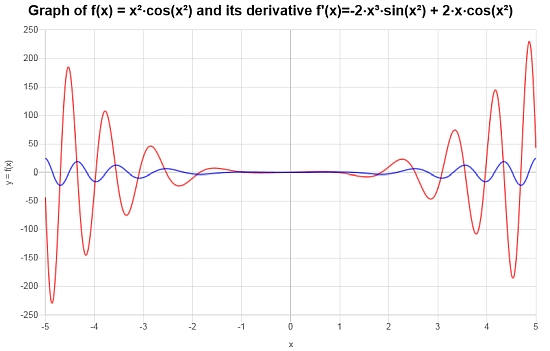
\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

该函数及其导数的相应图形如下所示。

例子。更多的导数规则

计算以下导数。\(\frac{d}{dx}\left( x \cos(x^2+1) \right)\)使用基本导数规则。

解决方案：现在,眼前的任务是对函数\(\displaystyle f(x)=x\cos\left(x^2+1\right)\)进行微分。

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

衍生规则的例子

对于函数\( f(x) = (x-1)(x^2+1) \),使用导数规则来寻找其导数。

解决方案：对于这最后一个例子,我们需要进行区分。\(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)。

最初的步骤。 在这种情况下,我们首先需要展开给定的函数\(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \),为了做到这一点,我们进行以下简化步骤。

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

扩大函数后,我们可以进行导数的计算。

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

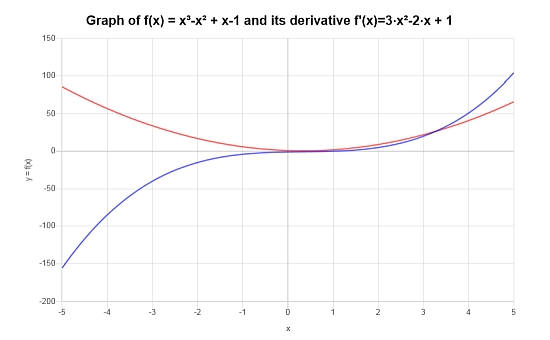
\(\displaystyle 3x^2-2x+1\)

从图形上看,这就是该函数及其导数的样子。