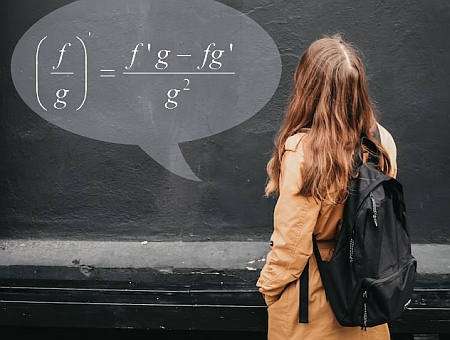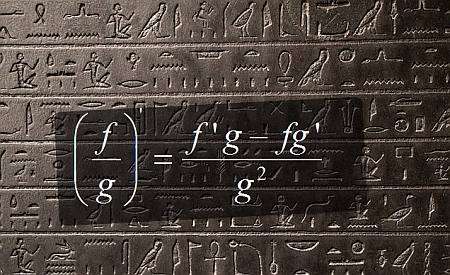商数规则
这个计算器可以让你对一个涉及商的函数使用商数法则,显示这个过程的所有步骤。你所需要提供的是一个有效的可微调函数。这个函数需要至少涉及一个商,以使商数规则适用。
一个有效函数的例子是f(x)=(x^2+2x+1)/(x^2-1),或者像f(x)=sin(x)/x,等等。
一旦提供了一个涉及商数的有效函数,你必须点击 "计算 "按钮以获得显示的计算步骤。
随之而来的是
产品规则
和
链条规则
, 这
商数规则
是一个最重要的基本
衍生品规则
.
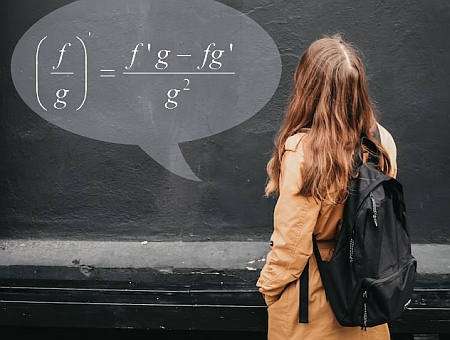
商数规则公式
简单的说,就是
商数规则
帮助你计算商的导数,使用各个函数及其导数的知识。商数规则的公式是
\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]
使用商数规则的步骤是什么?
-
步骤1:
明确指出进入商的分子和分母的函数f(x)和g(x)。
-
第2步:
简化任何可以简化的明显术语
-
第 3 步:
计算相应的导数f'(x)和g'(x)
-
第4步:
将步骤3中发现的数值插入公式\(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)中。
注意,f(x)和g(x)可能仍然是复数函数,所以你可能需要使用其他规则,如连锁规则来计算f'(x)和g'(x)。
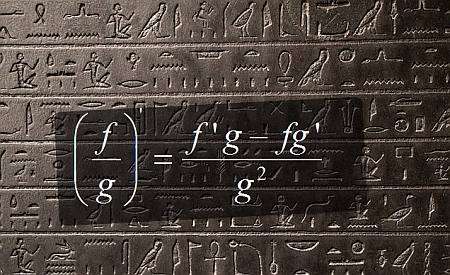
商数规则导数
在计算商数规则导数时,你是将商数的导数还原为单个导数的知识,但这些单个导数可能仍然需要许多步骤,并有
基本衍生品规则
要解决的问题。
这就是为什么微分被认为是一个 "直接 "的操作,但仍然需要充分组织和跟踪所有用导数规则分解时出现的碎片,然后继续处理那些可能需要应用更多微分规则的小碎片。
因此,你可能最终会有一个迭代的过程,但它保证会在某一点上结束,即深入到每个小部分,直到你找到一个基本的导数,如
多项式
或一个
三角形导数
.
微分中的商数规则
的作用。
微分中的商数规则
是相当重要的,这也是你为什么要用计算器来计算的一个很好的理由。在代数方面,商法则可以被认为比积法则更复杂,在很多情况下都是如此,但它最终取决于分子和分母中函数的复杂性。

商数规则实例
考虑一下函数。\(f(x) = \frac{x^2+1}{x-2}\),求其导数。
解决方案:
在这个例子中,我们需要分析函数\(\displaystyle f(x)=\frac{x^2+1}{x-2}\),寻找其导数。
\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)
By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)
By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)
Since the derivative of a constant is 0, we get that:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)
We already know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)
In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)
Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)
Removing unnecessary parentheses and multiplying the terms by \(-1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)
Aggregating those terms with \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)
Putting together the numerical values and operating the terms that were grouped with \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)
结论
:我们发现,给定函数的导数是。
\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]
因此,该函数及其导数的图形描述为\([-5, 5]\)。
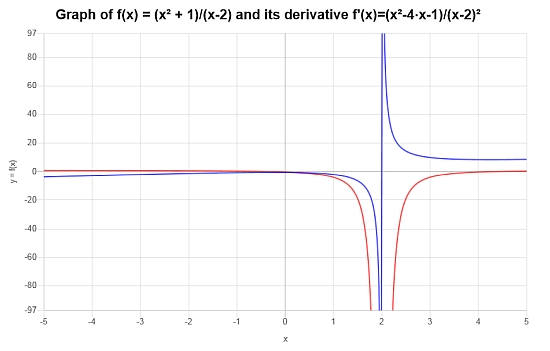
例子。商数规则的计算
现在考虑\(f(x) = \frac{x}{\sin(x)}\),用商数规则求其导数。
解决方案:
对于这第二个例子,我们感兴趣的函数是\(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\)。让我们用商数规则对其进行微分。
\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)
Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
We already know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)
By reorganizing/simplifying/expanding the terms that are amenable to
\( \displaystyle = \,\,\)
\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)
结论
:结论是,根据上述计算,导数由。
\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]
在图形上,我们可以看到函数(蓝色)和它的导数(红色)。
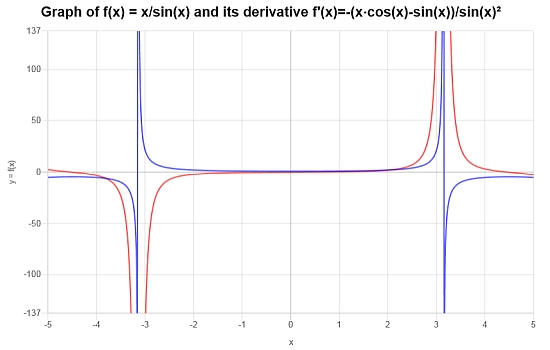
更多商数规则的例子
最后,考虑一下这个函数。\(f(x) = \frac{\sin(x)}{x^2}\),求其导数。
解决方案:
在最后这个商数规则的例子中,我们用函数\(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\)工作。.
\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)
The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)
We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)
By simplifying and regrouping terms
\( \displaystyle = \,\,\)
\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)
结论
:对于给定的函数,其导数是。
\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]
下图描述了\(f\)和\(f'\)的情况。
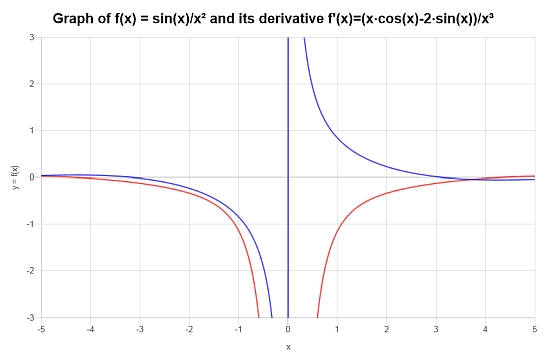
更多衍生品计算器
在微积分中,你将
寻找衍生品
在你所看到的任何地方。有成千上万的应用涉及它们,使它们成为科学和工程的最重要工具。
你将需要了解
隐性分化
对于不同的应用,往往涉及相关的速率,或者在多元微积分中,你会对以下内容感兴趣
寻找偏导数
.
总的来说,如果你能够正确地处理最常见的衍生品,你会发现你的生活更容易。
衍生品规则
,包括
链条规则
,以及
产品规则
和
商数规则
.