关于这个切线计算器

这个计算器将允许你无缝地进行计算,以获得一个函数的切线,在一个给定的点,显示所有的步骤。

你所需要做的就是提供一个有效的函数f(x),以及一个你想要切线的点。函数可以是任何有效的,可微调的函数,如f(x)=sin(x),或f(x)=x^2-x+1,等等。点可以是任何有效的数字表达式,比如说1/2。

然后,当提供了所需的信息,并且这些信息是有效的,你需要点击 "计算",以获得显示给你的切线方程的所有步骤。

切线在科学中的应用比比皆是。也叫 一阶或线性近似 在物理学和工程学中,它有一些非常深刻的意义,在那里,对变化的主要贡献（一阶部分）的想法是揭示了一个过程的许多信息。

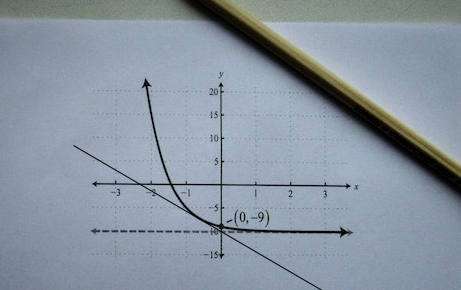
什么是切线

简单地说,切线是一条与曲线相交的线,但它只与曲线相交于一点（至少是局部）。这条切线是通过固定一个点\(x_0\),然后取一个不同的点\(x_1\)构建的。

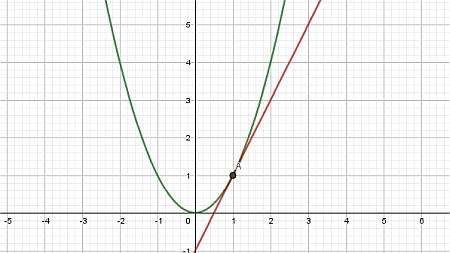
然后,通过构建通过点\((x_0, f(x_0))\)和\((x_1, f(x_1))\)的线,我们得到所谓的A 割裂线 ,如下图所示。

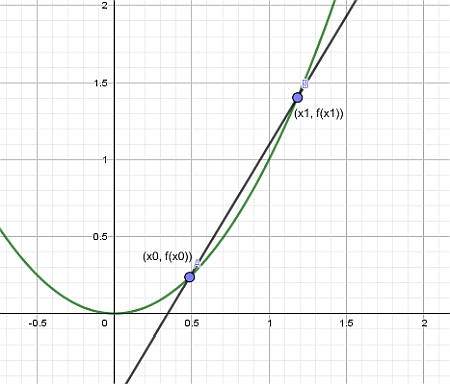
最后,我们让点\(x_1\)接近\(x_0\),我们得到的是切线：

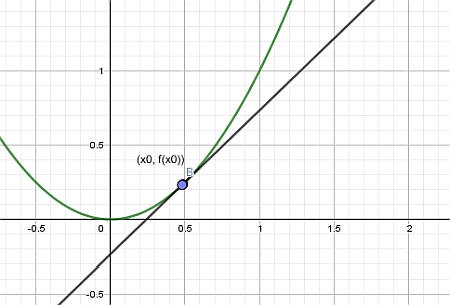
从几何学角度寻找切线的步骤

• 步骤1： 确定你要处理的函数f(x),以及点x0。你需要这两个点
• 第2步： 点（x0,f(x0)）将在函数f(x)的曲线上。绘制它
• 第3步： 选择一个点(x1,f(x1)),对于一个不同于x0的x1(可以是x的左边或右边)。绘制它
• 第4步： 画一条经过点（x0,f(x0)）和（x1,f(x1)）的直线
• 第5步： 选择一个位于x0和x1之间的点x2,画一条通过点（x0,f(x0)）和（x2,f(x2)）的直线。
• 第6步。 重复这个过程数次

这种图形方法可以帮助你大致了解切线的样子,但只是一种近似值（除非函数f（x）是线性的）。

切线公式

使用正切线的近似方法可以给你一个概念,但幸运的是,有一个精确的公式来计算一个函数在某一点\(x_0\)的正切线。正切线的公式是

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

很简单,是吧？简单地说,这个公式告诉我们,切线是一个 穿过点的直线 #\((x_0, f(x_0))\),其斜率为\(m = f'(x_0)\)。

那么,用简单的话来说,切线在某一点的斜率正是函数在该点的导数。

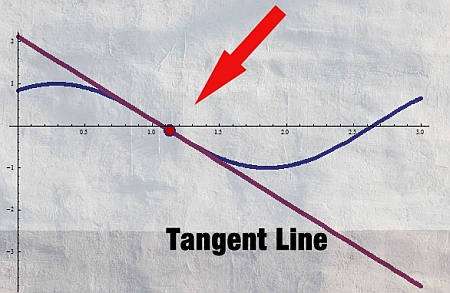
应用正切线公式的步骤

• 步骤1： 识别函数f(x)和点x0
• 第2步： 计算x0处的函数值,也就是f(x0)。
• 第3步： 计算f(x)在点x0的导数,所以你需要f'(x0)。
• 第4步： 直接应用切线的公式 \(y = f(x_0) + f'(x_0) (x - x_0)\)

一旦你有了 直线方程 你可以把它转化为对当前情况最有用的格式。

正切线的斜率

其中一个重要的启示是,切线在\(x_0\)处的斜率正好是\(f'(x_0)\),这是在\(x_0\)点的导数。这为导数提供了一个清晰和极其有用的几何术语解释。

这种联系可以通过简单地查看函数的导数来找到某条曲线在某一点的切线方程。

什么时候有一条水平切线？

当选择\(x_0\)的点时,当该点的相应导数等于零时,将出现一条水平切线。在这种情况下,切线（也就是在局部接触曲线的一点的线）将与Y轴平行。

因此,为了识别水平切线,你所需要知道的就是找到函数导数为零的点。

什么时候有垂直切线？

当导数在某一点是 "无限 "时,就会出现垂直切线。这是一种简单的说法,即在某一点上导数没有被定义,但当我们接近该点时,它就会收敛到无限大。

例如,可以说\(f(x) = \frac{1}{x}\)在x=0处有一条垂直的切线。不过,也可以说没有切线,因为导数在x=0处没有很好的定义。

例子。切线

求\(f(x) = x^2 - 2x + 1\)的切线方程,在点\(x_0 = 2\)。

解决方案： 下面这个函数是我们需要使用的：#\(\displaystyle f(x)=x^2-2x+1\)。首先,我们需要计算其导数。

该函数已经简化,所以我们可以直接计算其导数。

切线 :函数\(\displaystyle f(x)=x^2-2x+1\)在点\(x_0 = 2\)的切线方程为：

\[y = y_0 + f'(x_0)(x - x_0) \]

在这种情况下,\(\displaystyle y_0 = f(x_0)\),所以再把点\(x_0 = 2\)的值插入函数中,就可以得出：

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

另外,将点\(x_0 = 2\)的值插入计算出的导数中,可以得出：

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

那么,我们现在将这些数值插入切线公式中,就可以得到。

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

总结 :因此,可以发现,函数\(\displaystyle f(x)=x^2-2x+1\)在点\(x_0 = 2\)的切线是：

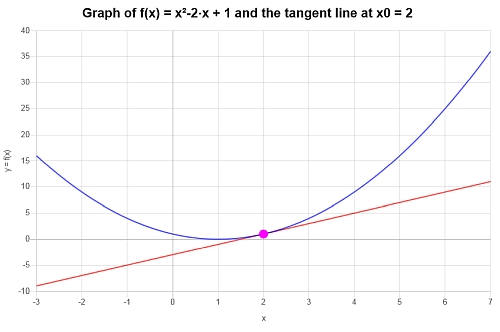
\[y = 2x-3 \]

对于给定的函数和它在\(x_0 = 2\)的切线,可以得到以下图：

例子。切线方程

对于函数\(f(x) = \sin(x) + 1\),在x=1/2处的切线是什么？

解决方案：

已经提供了以下函数：#\(\displaystyle f(x)=\sin\left(x\right)+1\),我们需要计算其导数。

该函数已经简化,所以我们可以直接计算其导数。

切线 :我们发现,在点\(x_0 = \frac{1}{2}\)处的切线的相应方程是由：

\[y = y_0 + f'(x_0)(x - x_0) \]

但在这个特定的情况下,\(\displaystyle y_0 = f(x_0)\),这意味着我们需要在函数中插入点\(x_0 = \frac{1}{2}\)的值,所以我们得到：

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

现在,对\(x_0 = \frac{1}{2}\)做同样的导数,我们发现

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

现在我们只需要把这些值插进去,所以我们发现

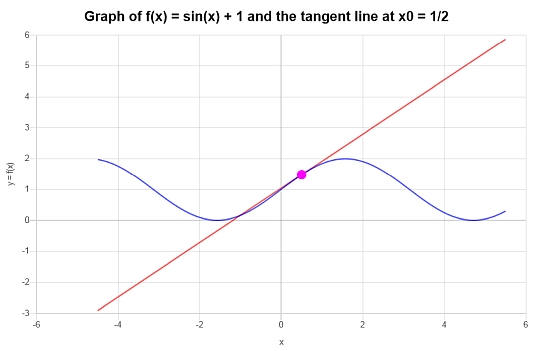
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

总结 :我们发现,我们要找的相应的切线,在相应的点\(x_0 = \frac{1}{2}\)处,由以下公式给出

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

在图形上。

例子。另一条切线

对于函数\(f(x) = \cos(x)\),在x=0处的切线是什么？这个结果有意义吗？

解决方案： 观察一下,\(f'(x) = -\sin(x)\),所以然后\(f'(0) = -\sin(0) = 0\)。这就是,切线在x=0处的斜率为m=0,那么切线的方程就是简单的\(y = y_0 = \cos(0) = 1\)。这很有意义,因为在这种情况下,切线是一条水平线。

更多差异化计算器

有些人可能会说,区分是一个相对简单的工作,用一个 衍生品计算器 可能不需要,但事实上,导数的计算仍然相当繁琐,可能需要很长的时间。 代数计算 .

当你有一个不止一个变量的表达式时,为了找到导数,你将需要确定这些变量是否相互独立,在这种情况下,你可以使用 部分导数 ,或者如果有一个方程将变量联系起来,在这种情况下,你将需要使用 隐性分化 .

微分学的主要两个领域是积分和微分,它们都有其广泛的应用,无处不在。 部分导数 在工程和经济领域的应用中出现了大量的内容。

一方面,微分处理的是无限小的变化率,而积分处理的是无限小的变化率的总和,令人钦佩的是,它们被紧密地联系在一起。 微积分的基本定理 .