线性近似计算法

这个 线性化计算器 将允许计算线性近似值,也被称为 切线 对于任何给定的有效函数,在一个给定的有效点。

你需要提供一个有效的函数,例如f(x)=x*sin(x),或f(x)=x^2-2x+1,或任何有效的可微调的函数,以及一个函数定义良好的点\(x_0\)。这个点可以是任何有效的数字表达式,比如说1/3。

一旦你提供了一个有效的函数和点,你点击 "计算",所有的计算结果就会为你显示出来。

线性近似或一阶近似是在给定的点\(x_0\)处寻找给定函数的线的近似。当然,对于曲线来说,线性近似将是粗糙的,不过主要的想法是,对于接近\(x_0\)的点来说,近似将是准确的。

线性近似

我们的想法是找到一条通过点\((x_0, f(x_0))\)的直线,它 "勉强接触 "函数\(f(x)\)。勉强接触 "的正式数学定义是由以下概念给出的 切线 ,为此我们需要 计算导数 的函数。

事实上,在点\(x_0\)的线性近似公式取决于导数\(f'(x_0)\),如下所示

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

这个 线性近似公式 基本上定义了 直线方程 通过点\((x_0, f(x_0))\),这就是为什么被称为 "线性近似",因为它定义了一个与\(f(x)\)在点\(x_0\)重合的线性函数,而且对于接近\(x_0\)的\(x\)值来说,它非常接近\(f(x)\)。

寻找线性近似值的步骤

• 步骤1： 你需要有一个给定的函数f(x)和一个点x0。该函数在x0处必须是可微的
• 第2步： 计算f(x0)和f'(x0),它们是函数f在点x0的函数和导数。
• 第3步： 将线性近似定义为y = f(x_0) + f'(x_0) (x - x_0),这就是上面提出的线性化公式

这条线,\(y = f(x_0) + f'(x_0) (x - x_0)\)代表一阶近似,也被称为局部线性近似。

与切线的联系

正如你现在可能已经怀疑的那样,线性近似与 切线 在给定的点。然后,计算线性近似值与计算切线完全相同

另一个名称是一阶近似,或切线近似,这也是微积分中常用的名称。

微分和线性近似

另一个常见的概念是微分,它与线性逼近的概念紧密相连,它只是它的一个推导。事实上,微分（或有限差分）被定义为\(\Delta y = y - f(x_0)\)。那么,根据一阶近似公式,微分的公式是

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

这自然与线性近似公式完全一样,只是术语\(f(x_0\)被传到了左边。

例子。计算一阶近似值。

考虑以下情况：#\(f(x) = x^2 - 2x + 3\),找到它在\(x_0 = 1\)的一阶近似值。

解决方案： 已经提供的函数是\(\displaystyle f(x)=x^2-2x+3\),我们需要找到围绕点x=1的线性近似值。因此,我们首先需要导数。

线性近似 :我们在\(x_0 = 2\)点寻找的线性近似方程由以下公式给出

\[y = y_0 + f'(x_0)(x - x_0) \]

注意,根据定义\(\displaystyle y_0 = f(x_0)\),这意味着我们需要在\(x_0 = 2\)点插入函数：

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

我们做同样的事情,但现在对于在\(x_0 = 2\)点的导数,所以,然后

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

现在有了这个,我们再来看看线性近似公式。

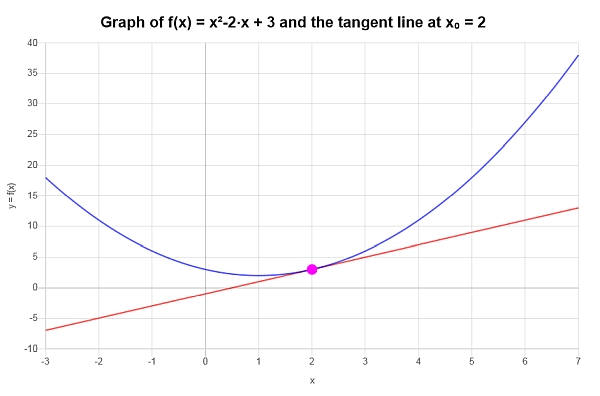
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

总结 :我们得出结论,\(\displaystyle f(x)=x^2-2x+3\)在\(x_0 = 2\)处的线性近似值是由：

\[y = 2x-1 \]

在图形上。

例子。更多的一阶近似

对于函数：#\(f(x) = x \sin(x)\)和点\(x_0 = 2\),找到相应的一阶近似值。

解决方案： 在这种情况下,我们需要工作的函数是：#\(\displaystyle f(x)=x\sin\left(x\right)\)。

我们现在计算其导数。

线性近似 :线性近似的方程是。

\[y = y_0 + f'(x_0)(x - x_0) \]

其中\(\displaystyle y_0 = f(x_0)\),所以接着我们计算：

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

对于\(x_0 = 2\)处的导数,我们发现：

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

现在我们准备把这些放回一阶近似公式中。

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

总结 :结论是,\(\displaystyle f(x)=x\sin\left(x\right)\)在给定点\(x_0 = 2\)的线性近似计算为：

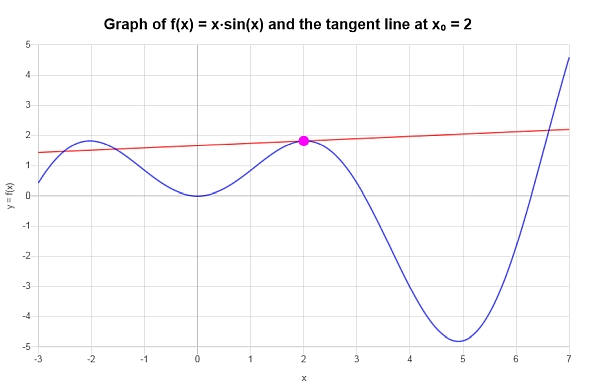
\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

从图形上看,我们可以得到以下图示。

例子。线性近似计算

计算\( f(x) = \frac{\sin(x)}{x}\)在\(x = \frac{\pi}{4}\)的一阶近似值。

解决方案： 已经提供了以下函数：#\(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\),我们需要计算其导数。

该函数已经简化,所以我们可以直接计算其导数。

一阶近似 :给定函数\(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\)在给定点\(x_0 = \frac{\pi}{4}\)的相应一阶近似方程由以下内容给出：

\[y = y_0 + f'(x_0)(x - x_0) \]

插入相应的数值。

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

因此,现在我们可以把这个放在公式中。

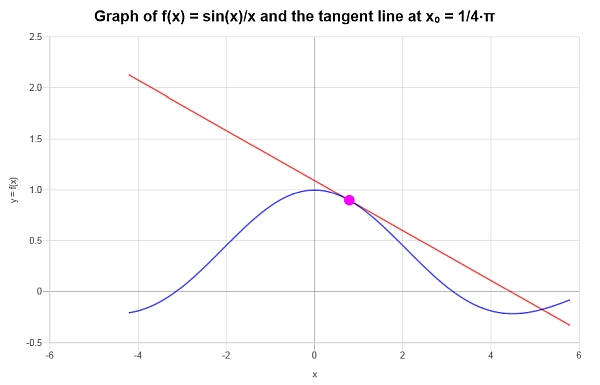
\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

总结 :因此,我们可以得出结论,给定的函数\(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\)在给定点\(x_0 = \frac{\pi}{4}\)的一阶近似值为

\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

以下是以图形方式得到的。

更多衍生品计算器

除此以外 线性化计算器 你可以找到很多基于导数做不同事情的软件。微分是微积分,物理学,工程和经济学中的一个重要操作,有广泛的应用。

还有一种方法是对更多的变量进行线性逼近,这是例如,对于一个函数\f(x, y)\),在这种情况下,线性逼近公式变成了\(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\),那么在这种情况下,为了找到线性化,我们需要使用 部分导数 .

寻找一个函数的线性化并不是到目前为止你能用导数做的唯一事情。微分是一个相对容易的操作,有简单的规则,如 产品规则 , 商数规则 和 链条规则 这使得衍生品的计算成为一个相对简单的操作。

虽然它应该是简单的,但它是一个好主意,可以使用 衍生品计算器 以获得所有显示的步骤,并明确提到所有的 衍生品规则 用过的。