隐式微分计算器

指示： 当 \(x\) 和 \(y\) 通过方程相连时,使用此隐式微分计算器计算导数 \(\frac{dy}{dx}\)。请在下面的表格框中提供一个涉及 x 和 y 的方程。

隐性分化

这个计算器将帮助你对涉及变量x和y的方程进行隐式微分。你需要提供一个有效的方程,如x^2 + y^2 = 1,或xy - x^2 y^2 = 0,等等。

一旦你提供了一个涉及两个变量（\(x\) 和 \(y\)）的有效方程,你只需点击 "计算 "按钮,相应的隐式微分的所有步骤就会显示出来。

这是一个带步骤的 dy/dx 计算器从这个意义上说,只要这两个变量在一个等式中相关联,它就会向您展示计算一个变量相对于另一个变量的导数的所有相关步骤。通过这种关系,您可以找到相应的 隐导数 .

有了将两个变量 \(x\) 和 \(y\) 联系起来的方程,我们就可以将 \(y\) 表述为 \(x\) 的函数,并写出 \(y = y(x)\)。通常,我们无法明确地将 \(y\) 表述为 \(x\) 的函数,而是假设存在这样的函数,在这种情况下,对 \(y\) 进行相对于 \(x\) 的微分是有意义的。

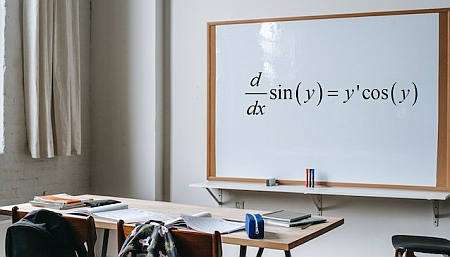
什么是隐性差异化？

隐式微分是一种微分计算该技术基于这样的假设,即可以从涉及 \(x\) 和 \(y\) 的给定方程中得出 \(y\) 是 \(x\) 的函数,尽管很多时候我们无法明确写出这样的函数。

一旦作出这一假设,我们就可以计算 \(\frac{dy}{dx}\),并使用所有已知的衍生品规则 ( 产品规则 , 商数规则和链条规则 ) 对方程两边进行微分,求出 \(\frac{dy}{dx}\)。

什么是隐式微分法？

隐式微分法是一种可以计算未直接以 \(f(x)\) 格式表示的表达式的导数的方法。例如,当给定一个变量 \(x\) 的函数时,我们只需对该函数进行微分即可。

但是,当两个变量 \(x\) 和 \(y\) 通过等式（例如 \(x^2+y^2 = 1\)）相关联时,您也可以将 y 相对于 x 进行微分,根据传统方法,您需要将 y 以 x 求解,然后才能进行微分。

使用隐式微分,只需假设 \(y = y(x\),并利用链条规则 .

使用隐性微分法的步骤

步骤1： 确定涉及两个变量x和y的方程,简化任何多余的条款
第2步： 假设y是x的一个函数,y=y(x),所以计算y相对于x的导数是有意义的
第3步： 计算导数的两边使用所有的衍生品规则你需要。这将导致在x,y和y'都存在的情况下,有可能出现一个平等。
第4步： 求解你在步骤3中得到的y'。注意,y'通常被写成x和y的函数,这很好,因为y也取决于x

这是一个非常普遍的方法,在不同的情况下会有细微的差别,但这是在大多数情况下应该可行的蓝图,并增加了潜在的代数操作难度。

为什么使用隐式微分计算器

隐式微分有时会让人困惑,如果你不太清楚你在微分什么,以及对什么变量进行微分。计算器可以帮助你比较你的结果,我们的计算器有一个特别之处,就是显示了这个过程的所有步骤。

这对你来说是一个至关重要的帮助,因为它将向你准确地展示什么是导数规则,以及你在哪里应用它。

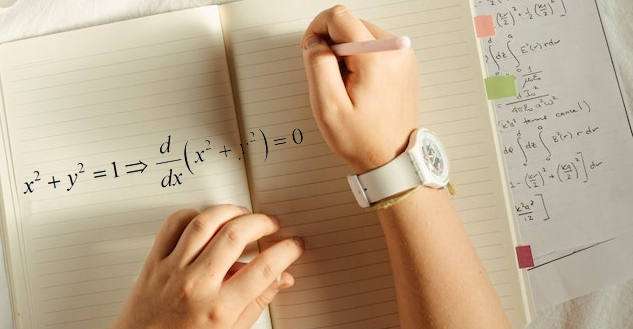
隐性分化的意义何在？

这是个公平的问题。如果你有一个涉及x和y的方程,为什么不用x来解y,而用常规的导数计算来得到y相对于x的导数。

原因1: 可能的情况是,你不可能明确地用x来解决y的问题。可能有一个函数,但你不能简单地找到它。想想看,y + tan(y) = x^2
原因2: 即使你碰巧求解y的x ,它可能是一个非常复杂的表达式,导数的计算可能非常曲折和困难。通常情况下,隐式微分在代数上是简单的,相对而言

隐性导数是否取决于y？

并不总是,但经常是。现在,这只是说 \(\frac{dy}{dx}\) 可以取决于 x 和 y,但因为 y 取决于 x,所以这只是说 \(\frac{dy}{dx}\) 一如所料取决于 x。

下一节将介绍不同的隐式微分例子。

二次隐含导数

一个问题是：能否使用隐式微分计算二阶导数？答案是肯定的。你只需像使用隐式微分法计算一阶导数一样,简单地假设 \(y\) 是 \(x\) 的函数,因此写出 \(y = y(x)\),然后就可以随心所欲地进行微分了。

例如,给定方程 \(x^2+y^2=1\),你想求出 \(\frac{d^2y}{dx^2}\)。以 \(x\) 为基准对两边进行微分：

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

现在,再次对 x 进行微分：

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

现在我们求出 \(y''\)：

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

例子。隐性差分实例

找出方程的 \(\frac{dy}{dx}\)：\(x^2 - y^2 = 2y\)

解决方案：这是一个隐式微分的例子。下面是一个方程：#我们需要进行隐式微分,假设 \(y\) 是 \(x\) 的函数。

该方程不需要进一步简化,所以我们可以继续进行隐式微分。

我们需要将方程两边与 \(x\) 进行微分,并假设两边都是 \(y = y(x)\)。

左侧 :左侧与 \(x\) 的差分

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

右侧 :将右边与 \(x\) 相乘

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

因此,以 \(x\) 为基准对两边进行微分,就得到了下面的结果：

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

把所有的条款放在一边。

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

将包含 \(\displaystyle \frac{dy}{dx}\) 的所有内容分组：

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

最后,求出 \(\displaystyle \frac{dy}{dx}\),得出

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

例子。更多隐性微分计算

点 \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) 与单位圆的切线的斜率是多少？

解决方案：请注意,单位圆的方程为 \(\displaystyle x^2 + y^2 = 1\),它隐含地定义了 \(y\) 作为 \(x\) 的函数。为了找到切线,我们需要计算指定点的 \(\frac{dy}{dx}\)。利用隐式微分,我们对定义单位圆的方程两边进行微分：\[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

兴趣点是 \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\),那么 .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

这意味着点 \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) 的切线斜率为 \(m = -1\),这意味着该点的切线方程为

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]