更多关于二次不等式

本二次不等式计算器将为您提供显示所有步骤的不等式解法。例如,您提供的不等式可以是 "x^2 - 1/2 > 0",一般来说,一元二次不等式不会太难解。

一旦您提供了一个有效的不等式,其中涉及 二次表达式 您可以点击 "计算 "来显示计算的所有步骤,包括不等式解的图形。

二次不等式 与 线性不等式 ),就能保证找到精确的解,而这一过程涉及解一元二次方程。

这种不平等的定义是什么？

我们没有明确说明这一点,但从它的名字就可以看出：二次不等式是一种特定类型的不等式,其中涉及的所有项都是最多 2 度的多项式。 在这种情况下,一个例子是

\[\displaystyle x^2 < x - 1\]

由于不等式两边都是最多 2 阶的多项式,所以是二次型：

\[\displaystyle x^2 < x^3 - 1\]

那么这个不等式就不再是二次不等式了,因为右边有一个项 \(x^3\)。对于这些不等式,我们有一个清晰的求解路线图。

求解二次不等式的步骤

• 步骤1： 请确保您遇到的是一元二次不等式,因为本例中使用的方法仅对此类不等式有效
• 第2步： 与大多数不等式一样,将所有内容传递到不等式的左边,然后求解相关方程
• 第3步： 如果相关的一元二次方程没有实数根,我们就知道要么整个实线是解,要么没有解。因此,你可以测试任意一点,看它是否解了不等式,如果解了,解就是整条实线（-∞,∞）,否则,解就是空的。
• 第4步： 如果相关的一元二次方程只有一个实数解,则意味着相关的二次曲线图形与 x 轴相切。因此,根据不等号的不同,可能只有接触点是解,也可能除了接触点以外的所有点都是解,还可能是整条实线（-∞,∞）,为此需要检验接触点和接触点以外的点（接触点的左右两边）。
• 第4步： 如果相关的一元二次方程有两个不同的实数解,则需要检查这些根定义的区间,以确定实线的哪些部分是解的一部分

分析完这些片段后,如果需要,可以使用 "union "运算符将它们连接起来,该运算符用于将区间拼接在一起。

如何画二次不等式？

不等式作图 提供了一种直观了解解法的好方法。就程序而言,你需要知道自己是在处理单变量不等式,还是在处理多变量不等式。

如果有这样的不等式

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

如果只有一个变量,那么解就会是实线的一个子集。另一方面,如果你有类似于

\[\displaystyle y < x^2 - \frac{1}{2} x \]

那么只有 x 和 y 两个变量,不等式的解就是 x-y 平面的一个子集。

二次表达式的重要性

方程和不等式中涉及的二次表达式在数学中起着重要作用。也许,二次表达式是继线性表达式之后使用最广泛的结构类型。

在学习微积分和代数时,你会发现二次函数在最大化,最小化,积分等问题中的应用数不胜数。深入研究一下,你会发现二次表达式的应用遍及各种科学显示领域

例题二次不等式

求解这个二次不等式：\(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

解决方案：

我们需要先求解下面的辅助二次方程 \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\)。

应用二次公式

一元二次方程为

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

在这种情况下,我们有

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

将这些数值代入根的计算公式,我们就得出了结果：

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

因此,我们发现。

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

关键点

发现的临界点列表按升序排列为\(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

然后,我们需要分析以下临界区间：

- 对于区间 \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\)：左侧为正值,因此 \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) 不属于解的一部分。

- 对于区间 \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\)：左侧为负数,这意味着 \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) 是解的一部分。

- 对于区间 \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\)：左侧为正值,这意味着 \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) 不属于解的一部分。

解决方案

根据所提供的不等式并分析临界点,我们发现不等式的解是\(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\)。

使用区间符号,可将解法写成

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]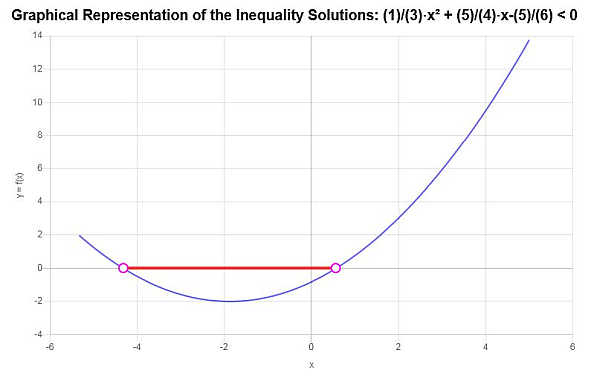

例题：更多二次不等式

解决：\(x^2 < 4\)

解决方案：

给出的不等式是

\[x^2 < 4\]

得出二次方程 \(\displaystyle x^2-4=0\)。

二次方程

对于形式为 \(a x^2 + bx + c = 0\) 的一元二次方程,根的计算方法如下 二次方程 :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

在这种情况下,我们需要求解的方程是 \(\displaystyle x^2-4 = 0\),这意味着相应的系数是：

\[a = 1\] \[b = 0\] \[c = -4\]

首先,我们将计算判别式以评估根的性质。判别式的计算方法是：。

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

因为在这种情况下,我们得到的判别式是 \(\Delta = \displaystyle 16 > 0\),是正值,所以我们知道方程有两个不同的实数根。

现在,将这些数值插入到根的公式中,我们可以得到。

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

因此,我们发现。

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

在这种情况下,一元二次方程 \( \displaystyle x^2-4 = 0 \),有两个实数根,所以：

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

这样,原多项式就被因子化为 \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \),从而完成了因子化。

分析关键点

发现的临界点列表按升序排列为\(-2\), \(2\).

在此基础上,我们需要对以下区间进行分析：

- 对于区间 \(\left(-\infty, -2\right)\)：左侧为正值,因此 \(\left(-\infty, -2\right)\) 不属于解的一部分。

- 对于区间 \(\left(-2, 2\right)\)：左侧为负数,因此 \(\left(-2, 2\right)\) 是解的一部分。

- 对于区间 \(\left(2, \infty\right)\)：左侧为正值,这意味着 \(\left(2, \infty\right)\) 不属于解的一部分。

不等式的解决方案

根据所提供的不等式并分析临界点,我们发现不等式的解是\(-2< x \le 2\)。

使用区间符号,可将解法写成

\[\left[-2,2\right)\]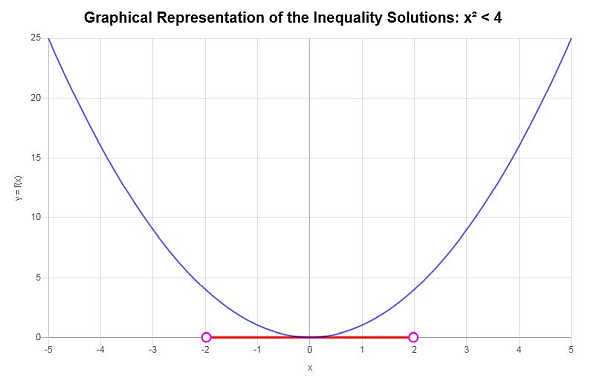

其他有用的不等式计算器

最简单的不等式类型是 线性不等式 .在这之后,就可以轻松地进行一元二次不等式计算了。

然后,你有 多项式不等式 一般来说,度数大于 2 的问题应该是简单明了的,但就解决这些问题所需的工作量而言,它们仍可能是一项艰巨的任务。

拥有 不等式计算器 在一般不等式中,它能真正派上用场,因为它能解决不同类型的不等式,而这些不等式都适合精确解的搜索。