二次方程。如何解决一元二次方程的问题？

二次方程是一个形式的方程。

\[a x^2 + b x + c = 0\]

与\( a \neq 0\)。这是决定一个的主要公式 二次方程 .

好消息是,上述方程并不难解,考虑到二次方程在代数,微积分和几乎所有地方都出现,这是一件好事。

二次方程的解决方法

现在,问题是如何解决这个二次方程。幸运的是,答案简单且众所周知：它有如下形式的解

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

这些被称为 二次方程的根 (也被称为方程的解）。为了分析解的性质,判别式被定义为：。

\[D = b^2 - 4ac\]

二次方程的解决方案的类型

根据判别式的值,定义了解决方案的性质。事实上,当\(D > 0\)时,则有两个不同的实数解,当\(D = 0\)时,有一个重复的实数解,而当\(D < 0\)时,有两个不同的虚数解。这 二次方程求解器 帮助你自动进行这些计算。

这个二次方程求解器的一个好处是,它将显示计算y截距的步骤,顶点的坐标,并绘制出二次函数的图样。

.

二次方公式步骤

为了成功解决一元二次方程,你必须遵循几个步骤。

第1步：确定系数。 检查给定的\(ax^2+bx+c\)形式的方程,并确定系数\(a\),\(b\)和\(c\)。系数\(a\)是与二次项\(x^2\)相乘的系数。系数\(b\)是与线性项\(x\)相乘的系数,而系数\(c\)是常数。

例子：假设你有以下表达式：\(x^2+3x+1\)。系数是什么？在这种情况下,\(a = 1\)（乘以二次项\(x^2\)的系数）,\(b = 3\)（乘以线性项\(x\)的系数）,和\(c = 1\)（常数）。

例子：假设你有以下表达式,如何？\(\frac{5}{4} + \frac{3}{4} x + \frac{1}{2} x^2\).现在的系数是多少？在这种情况下,\(a = \frac{1}{2}\)（乘以二次项\(x^2\)的系数）,\(b = \frac{3}{4}\)（乘以线性项\(x\)的系数）,和\(c = \frac{5}{4}\)（常数）。

例子：下面的表达方式会发生什么：\(-3 + \frac{1}{2} x\)。在这种情况下,我们有\(a = 0\),因为这个表达式不包含二次项\(x^2\),所以在这种情况下,这不是一个二次项表达。

第2步：将你找到的系数插入公式中。 该公式为二次方程,即

\[x = \displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

所以你需要替换系数\(a\),\(b\)和\(c\)的值。

例如：如果你有一个方程式：#\(-3x^2 + 2x-1 = 0\),你发现\(a = -3\),\(b = 2\)和\(c = -1\)。因此,将这些数值插入公式中,我们得到：

\[x = \displaystyle\frac{-2 \pm \sqrt{2^2 - 4(-3)(-1)}}{2(-3)}\]

第3步：简化方程中的数值,一旦你插入了\(a\),\(b\)和\(c\)的数值,就可以简化。 .在前面的例子中,我们会有

\[x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}\]

第四步：查看平方根的内部。 如果该值为正,那么 二次方程 有两个实数根。如果数值为0,那么就有一个实数根,如果平方根里面的数值为负数,那么就有两个复数根。在前面的例子中,我们的平方根里面有一个-8,所以我们有两个复数解,如下图所示。

\[x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}= \frac{-2 \pm i \sqrt{8}}{-6}\]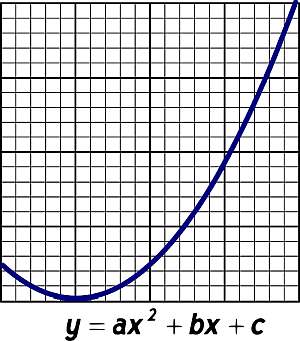

二次方公式的用途是什么

这 二次方程 是数学中最普遍的公式之一。它出现在你解决各种几何问题的时候,比如当你在给定一个固定周长的情况下使面积最大化,或者在许多文字问题中出现。

很多人想知道这个一元二次方程公式和 "一元 "方法之间是否有什么关系。 完善广场 .答案很简单：你通过以下方式得出二次方程 求解一元二次方程 通过完成平方。这与我们所知道的二次方程的想法完全相同。

请注意,一元二次方程的解有一个非常有趣的几何特性：当你计算找到的解的平均值时,你会得到抛物线顶点的X坐标,这有助于你找到 顶点形式 抛物线的标准形式,也被称为标准形式,在许多应用中使用,例如与锥形截面的形式。

二次方程的例子

计算以下一元二次方程的根：\(3x^2 - 2x + 4 = 0\)

解决方案：

需要解出以下方程。

\[ 3 x^2 -2 x + 4 = 0\]

这对应的是一个二次方程。下面的公式是用来寻找解决方案的。

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

使用上述公式,我们可以得到：。

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-2) \pm \sqrt{ (-2)^2 - 4(3)(4)}}{2(3)}\]\[= \frac{ 2 \pm \sqrt{ -44}}{ 6}\]

因此,解决方案是。

\[x_1 = 0.333 - 1.106 i \] \[x_2 = 0.333 + 1.106 i \]

因此,有两个虚解\(x_1 = 0.333 - 1.106 i \)和\(x_2 = 0.333 + 1.106 i \)。

另外,Y截点出现在\(y = 4\),这意味着Y截点的坐标是\((0, 4)\)。

最后,顶点的坐标是。

\[x_V = \frac{-b}{2a} = \frac{-(-2)}{2\cdot 3} = 0.3333\] \[y_V = f(x_V) = 3 (0.3333)^2 -2 (0.3333) + 4 = 3.6667\]