关于解不等式的更多信息

有了这款计算器,您就可以解决您提供的不等式问题。您只需在框中输入所需的不等式,并确保您提供的是有效的不等式。

例如,您可以提供类似 "2x^2 - x >= 1/2" 或类似 "sin(x) > 0 "的内容,只要提供有效的内容即可。还要确保使用不等号,如">","<", ">="或"<="。

如果使用"=",则该计算器将充当 方程计算器 .

一旦你提供了一个有效的不等式,下一步就是点击 "求解",几分之一秒钟后,你就会看到逐步求解的过程。需要注意的是：并不是所有的不等式都能被求解,请牢记这一点。

并不是所有的不等式都很容易求解,我们也不能采用一些先入为主的方法。只有某些类型的不等式,如 线性不等式 , 二次不等式 或 多项式等式 (学位较低者）接受系统的治疗。

什么是不平等？

不等式是一种数学对象,与 数学方程 不同的是,不等式不包含"=",而是包含">","<", ">="或"<="。与方程相比,不等式在外观上的这一细微差别仍然增加了解不等式的复杂性。

例如,下面的表达式是一个不等式

\[\displaystyle x + \frac{1}{3} < x^2 \]

因此,它是一个有两边的数学表达式,即左边和右边,并以"<"作为相应的不等号。上面的不等式被称为二次不等式,因为左右两边的表达式都是多项式,而且最高度数是 2。

例如,下面的不等式是一个三角不等式：

\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]

这是一个不等式,因为它有不等号 \(\le\),右边包含一个 三角表达式 .请注意,第一个不等式的解法非常简单,而另一个不等式的解法却远非如此简单,实际上你根本无法解出它。

如何解不等式

一般来说,我们会先求解相关的方程,从而找到不等式的解。当相关方程更难解时,不等式的解就更难。下面的步骤将有助于你的求解过程：

看似复杂,其实只要有条不紊地进行即可。例如,如果你的不等式是 \(\displaystyle x + \frac{1}{3} < x^2 \),那么相关的方程就是 \(\displaystyle x + \frac{1}{3} = x^2 \),这很容易求解,因为它是一个 二次方程 .

那么,在分析临界点（如果有的话）时, 不等式解的作图 可能会让事情更清楚。在一些代数课程中,他们会教学生使用表格来记录临界点之间发生的事情,这可能会非常有用。

与不等式系统有什么区别？

不等式系统由几个需要同时求解的不等式组成。它听起来比解一个简单的不等式更难,因为它更难。如果说解不等式是一件费力的事,那么解不等式系就更费力了。

下面是一个不等式系统的例子：

\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]

在上面的示例中,您有一个 不等式系统 来求解。这个不等式系统有两个不等式和两个未知数（x 和 y）。

正如你可能想象的那样,解不等式系一般来说是很困难的。我们将主要关注线性方程组的解法,这与 解线性方程组

使用这个带步骤的不等式计算器的优势

实际上,求解大多数不等式都很困难。只有少数结构非常特殊的不等式才适合分析。大多数不适合,所以你最好对此有所准备。

• 优势1。 节省大量时间求解不等式可能需要很长时间,因为您首先需要求解相关方程,然后分析临界点
• 优势2。 确保你能尽最大努力去解决它：您现在可能已经知道,并非所有方程或不等式都能轻松求解,或者根本无法求解。带步骤的计算器会根据检测到的结构尝试最佳方法。
• 优势3。 以简洁的方式逐步获取结果。有些计算器会给出最终答案,但不会显示步骤。描述解法的图表也很有用

在你学习的过程中,如果有一个不等式计算器能帮你完成繁重的工作,那么它就会向你展示如何完成工作,而且你很可能会掌握所需的技能来检测那些更容易处理的结构。

不等式有什么实际用途吗？

没错！基础数学（代数和微积分 101）更强调等式和方程。现实世界中有很多过程,我们不一定有等式,但我们确实有不等式,这些不等式来自于一些物理约束条件施加的下限或上限。

某些高等数学领域,如微分方程,其理论框架是建立在不等式基础上的（在某些情况下,专家们喜欢称之为 "能量估计"）。

不等式的重要性可能并不明显,学习不等式的必要性也并不迫切,但事实上,不等式的确是构建理论的数学方法的基石之一,尽管在漂亮的最终结果中,我们往往看到的是等式。

例题解不等式

计算解决方案：\(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)

解决方案： 我们需要把不等式的所有项都放在左侧（也可以放在右侧,但常规做法是放在左侧）：

\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]

根据上述不等式,我们可以得到需要首先求解的相关线性方程：

\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]

第0步。 在这种情况下,我们首先需要对给定的线性方程进行化简,为此,我们要执行以下化简步骤：

解线性方程

将 \(x\) 放在左侧,常数放在右侧,我们得到

\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]

现在,用方程两边除以 \(\frac{1}{3}\),求解 \(x\),得到如下结果

\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]

并简化我们最终得到以下

\[\displaystyle x=-\frac{13}{4}\]

因此,对给定的线性方程求解 \(x\) 就会得到 \(x=-\frac{13}{4}\)。

关键点分析

发现的唯一临界点是 \(-\frac{13}{4}\)。

在此基础上,我们需要对以下区间进行分析：

- 对于区间 \(\left(-\infty, -\frac{13}{4}\right)\)：左侧为负数,因此 \(\left(-\infty, -\frac{13}{4}\right)\) 不在解的范围内。

- 对于区间 \(\left(-\frac{13}{4}, \infty\right)\)：左侧为正,这意味着 \(\left(-\frac{13}{4}, \infty\right)\) 是解的一部分。

不等式的解决方案

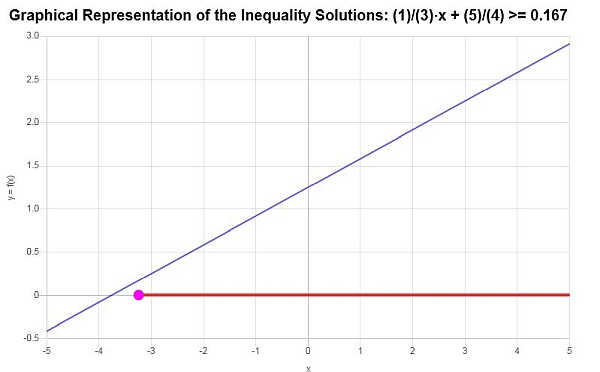
根据所提供的不等式并分析临界点,我们发现不等式的解是\(x \ge -\frac{13}{4}\)。

使用区间符号,可将解法写成

\[\left[-\frac{13}{4},\infty\right)\]

这 线性不等式图 得到的解决方案如下所示

实例：更多不平等示例

求下列题目的解：\(\sin(x) > 0\)

解决方案： 下面是需要求解的三角不等式：

\[\sin\left(x\right) > 0\]

处理辅助方程

根据上述三角不等式,我们可以得到需要先求解的相关方程：

\[\sin\left(x\right)=0\]

求解辅助三角方程

那么解就是对于任意整数常数 \(K\),解为 \(x = \pi{}K\)。

关键点分析

根据辅助方程的解,找到的临界点列表为对于任意整数常数 \(K\),临界点为 \(\pi{}K\)。

请注意,我们有无数个临界区间,因此我们将在下文中对其中一些区间进行分析：

- 对于区间 \(\left(-3\pi{}, -2\pi{}\right)\)：左侧为负数,因此 \(\left(-3\pi{}, -2\pi{}\right)\) 不在解的范围内。

- 对于区间 \(\left(-2\pi{}, -\pi{}\right)\)：左侧为正,这意味着 \(\left(-2\pi{}, -\pi{}\right)\) 是解的一部分。

- 对于区间 \(\left(-\pi{}, 0\right)\)：左侧为负数,这意味着 \(\left(-\pi{}, 0\right)\) 不属于解的一部分。

- 对于区间 \(\left(0, \pi{}\right)\)：左侧为正,这意味着 \(\left(0, \pi{}\right)\) 是解的一部分。

- 对于区间 \(\left(\pi{}, 2\pi{}\right)\)：左侧为负数,因此 \(\left(\pi{}, 2\pi{}\right)\) 不是解的一部分。

- 对于区间 \(\left(2\pi{}, 3\pi{}\right)\)：左侧为正,这意味着 \(\left(2\pi{}, 3\pi{}\right)\) 是解的一部分。

这就是我们对整个区间序列的处理方式。

零件溶液间隔

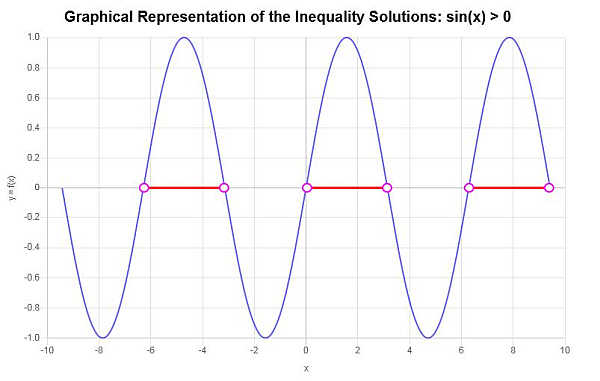
根据对找到的临界点和连续临界点产生的相应区间的分析,我们可以确定以下内容是不等式解的一部分：

\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]

在这种情况下,我们可以大致确定不同的解决方案区域,如下图所示。图 不等式图 得出的解法图示如下：

举例说明：更多不等式

求解二次不等式 \( x^2 - 2x > 6 \)。

解决方案： 我们需要求解的不等式是

\[x^2-2x > 6\]

将不等式的所有项放在一边,我们得到

\[x^2-2x-6>0\]

辅助方程

我们需要先求解下面的辅助方程：

\[x^2-2x-6=0\]

我们左边有一个多项式表达式,它是 \(\displaystyle deg(p) = 2\),它的前导系数是 \(\displaystyle a_{2} = 1\),它的常数系数是 \(\displaystyle a_0 = -6\)。

二次方程

在这种情况下,根的计算公式如下：

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]

因此,我们发现。

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]

在这种情况下,一元二次方程 \( \displaystyle x^2-2x-6 = 0 \) 有两个实数根,这两个实数根成为临界点：

关键点分析

发现的临界点列表按升序排列为\(-\sqrt{7}+1\), \(\sqrt{7}+1\).

在此基础上,我们需要对以下区间进行分析：

- 对于区间 \(\left(-\infty, -\sqrt{7}+1\right)\)：左侧为正,这意味着 \(\left(-\infty, -\sqrt{7}+1\right)\) 是解的一部分。

- 对于区间 \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\)：左侧为负数,因此 \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) 不在解的范围内。

- 对于区间 \(\left(\sqrt{7}+1, \infty\right)\)：左侧为正,这意味着 \(\left(\sqrt{7}+1, \infty\right)\) 是解的一部分。

求不等式的解

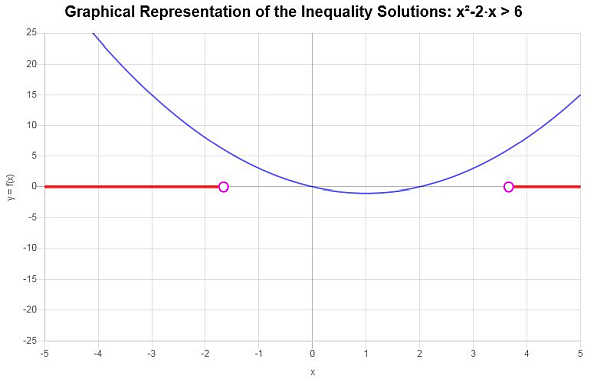
根据所提供的不等式并分析临界点,我们发现不等式的解是\(x < -\sqrt{7}+1\) 或 \(x > \sqrt{7}+1\)。

使用区间符号,可将解法写成

\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]

不等式的解以图形表示：

更多上述不等式

您总是从 线性不等式计算器 或者 二次不等式计算器 因为只有这些人才能保证提供解决方案。

那么,即使有 多项式不等式 因为多项式不等式也会变得棘手,甚至无法用基本方法精确求解。

任何其他类型的不等式都取决于它的结构和你能想出的一些巧妙的替换。