Подробнее о формуле наклона

Этот Формула наклона калькулятор позволит вам вычислить наклон для двух заданных точек вида (x, y) по известной формуле, показывая все шаги.

Вам нужно указать две точки вида (x, y). Например, вы можете указать точки типа (1/2, 1/3), или что-то не упрощенное типа (1/3+1/4, sqrt(8)).

После того, как вы предоставите две достоверные точки вида (x, y), следующим шагом будет нажатие на кнопку с надписью "Рассчитать", и вам будут предоставлены все шаги вычисления формулы наклона.

Понятие уклона является важнейшим в алгебре и геометрии, и уклон очень важен для построения линейная функция .

Какова формула наклона?

Предположим, что на плоскости имеются две точки \((x_1, y_1)\) и \((x_2, y_2)\). Тогда Формула наклона это

\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]

Некоторые люди скажут: "Это отношение между разностью у и разностью х", с оговоркой, что при выполнении разностей нужно сохранять порядок. Если сверху вы делаете \(y_2 - y_1\), то снизу вы делаете \(x_2 - x_1\), а не \(x_1 - x_2\).

Также некоторые люди называют эту формулу наклона "подъем против бега"

Каковы шаги для использования формулы наклона

• Шаг 1: Определите две заданные точки. Перед использованием формулы желательно максимально упростить выражения
• Шаг 2: Определите, какая точка является первой, а какая второй. Выбор не имеет значения для результата, при условии, что вы остаетесь последовательны в своем выборе
• Шаг 3: Используйте формулу \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\), подставляя значения первой точки \(x_1\) и \(y_1\), и второй точки \(x_2\) и \(y_2\)
• Шаг 4: После вставки значений упростите, насколько это возможно, чтобы свести наклон к его простейшей форме

Вычисление наклона по формуле обычно очень простой процесс, просто следите за тем, чтобы порядок точек был последовательным.

Как использовать наклон?

Наклон - это мера наклона линии. Действительно, когда у вас есть линейная функция вида

\[y = m x + n\]

тогда наклон линии равен m. Вышеуказанное известно как форма пересечения наклона линии.

Каковы шаги для использования наклона для линии?

• Шаг 1: Определите наклон m. Упростите его как можно больше
• Шаг 2: Вам нужно знать y-пересечение, то есть точку на оси y, когда линия пересекает ее, и назовем ее n
• Шаг 3: Тогда уравнение линии будет \(y = m x + n\)

Существуют и другие формы выражения линии, кроме Наклонный перехват . У вас есть стандартная форма линии , и Точечно-наклонная форма .

Как использовать формулу "наклон-пересечение

Это центр линейные функции (или, лучше сказать, линейный аффинный) и линейные графики. Действительно, когда у вас есть наклон m и y-перехват n, вы можете непосредственно вычислить уравнение линии как y = mx + n.

Геометрически это довольно просто интерпретировать, так как y-пересечение абсолютно понятно как точка пересечения линии с осью y, а наклон - это мера наклона. Для сравнения, наклон m = 1 соответствует наклону 45 ^О .

И наоборот, если у вас есть линейная функция через Алгебраическое упрощение вы всегда можете свести к форме с перехватом y = mx + n, и тогда вы найдете наклон m и перехват n.

Пример: использование формулы наклона

Вычислите наклон для следующих точек: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) и \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)

Отвечать: Нам нужно вычислить наклон прямой, проходящей через точки \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) и \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).

Для вычисления наклона, заданного двумя точками, требуется следующая формула:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Теперь, подставляя значения точек \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) и \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\), получаем:

Отсюда делаем вывод, что наклон прямой, проходящей через точки \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) и \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\), равен \(m = \displaystyle \frac{1}{4}\).

Пример: другие примеры формулы наклона

С помощью формулы наклона найдите наклон прямой, проходящей через точки: \((2, 4)\) и \((5, 12)\)

Отвечать: В данном случае у нас есть точки \(\displaystyle (x_1, y_1) = \left(2,4\right)\) и \(\displaystyle (x_2, y_2) = \left(5,12\right)\), через которые, как мы знаем, проходит прямая.

Формула наклона такова:

\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]

Теперь, подставляя значения точек \(\displaystyle (x_1, y_1) = \left(2,4\right)\) и \(\displaystyle (x_2, y_2) = \left(5,12\right)\), получаем:

Отсюда делаем вывод, что наклон прямой, проходящей через точки \(\displaystyle (x_1, y_1) = \left(2,4\right)\) и \(\displaystyle (x_2, y_2) = \left(5,12\right)\), равен \(m = \displaystyle \frac{8}{3}\).

Пример: форма интерцепта склона

Найдите форму интерцепта наклона для следующей прямой: \(2x + 4y = 3 + \frac{1}{2}x\).

Отвечать: Мы имеем следующее уравнение:

\[\displaystyle 2x+4y=3+\frac{1}{2}x\]

Помещая \(y\) в левую часть и \(x\) и константу в правую часть, мы получаем

\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]

Теперь член, умножающий \(y\), равен \( 4 - 0 = 4\), а так как \( \frac{1}{2} - 2 = -\frac{3}{2}\), то получается следующее

\[\displaystyle 4y=-\frac{3}{2}x+3\]

Теперь, находя \(y\) путем деления обеих частей уравнения на \(4\), получается следующее

\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]

и упрощая окончательно получаем следующее

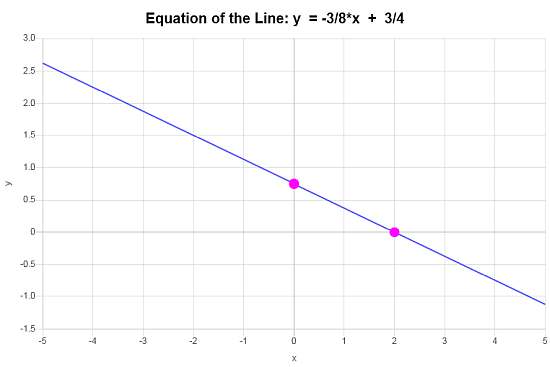
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]

Вывод : На основании предоставленных данных мы заключаем, что уравнение линии в форме наклона-отрезка имеет вид \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), с наклоном \(\displaystyle b = -\frac{3}{8}\) и точкой пересечения по оси y \(\displaystyle n = \frac{3}{4}\).

Графически линия выглядит следующим образом:

Другие калькуляторы линейных функций

Вместе с квадратичные функции линейные функции являются одними из самых важных объектов в математике. Вы можете вычислить наклон линии, найти угол наклона линии, найти угол наклона линии перпендикулярная линия , и преобразовывать линию в различные формы, в зависимости от потребностей.

Примечательно, что для линейных функций легче найти обратные линейные функции так как большинство линейных функций относятся 1 к 1 (за исключением горизонтальных линий).