Подробнее о триггерных производных

Используйте этот калькулятор, чтобы найти тригонометрические производные, которые в данном случае мы предполагаем, чтобы быть любой допустимой дифференцируемой функцией, которая включает одну или несколько элементарных тригонометрических функций.

Одним из примеров действительной функции для этого калькулятора является f(x) = sin(x)/x или f(x) = x*sin(x^3), просто для примера.

Затем, когда вы уже набрали соответствующую функцию, вы можете нажать кнопку "Рассчитать", чтобы получить все шаги расчета показанной вам производной.

Тригонометрические функции играют решающую роль в исчислении, а также в расчет производных в общем. В конечном счете, более сложные функции могут свести свои производные к вычислению производной для более простых тригонометрических функций.

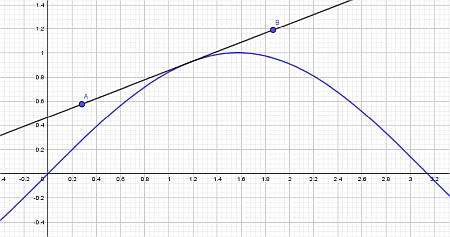
Основные производные триггера

Идея использования производных правил состоит в том, чтобы разбить сложную функцию и дифференцировать ее, используя производные известных функций. В частности, важную роль в этом будут играть простые тригонометрические функции, такие как синус, косинус, тангенс и котангенс.

Каковы основные производные триггера?

• Триггерная Производная 1: \(\frac{d}{dx} \sin (x) = \cos(x)\)
• Триггерная Производная 2: \(\frac{d}{dx} \cos (x) = -\sin(x)\)
• Триггерная Производная 3: \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
• Триггерная Производная 4: \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
• Триггерная Производная 5: \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
• Триггерная Производная 6: \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

Это основные производные, которые вам нужно очень хорошо знать и, возможно, запомнить, чтобы использовать Правила производных для вычисления более сложных производных

Являются ли триггерные производные в градусах?

Нет, производная тригонометрических функций находится в радианы , поэтому найденные тригонометрические производные отражают тот факт, что аргумент x измеряется в радианах.

Так, например, предположим, что мы хотели вычислить производную sin в градусы , поэтому мы определяем \(f(y) = \sin(y)\), где \(y\) измеряется в градусах.

Теперь пусть \(x = \frac{\pi y}{180}\) будет эквивалентным углом в радианах, а также решая для \(y\), мы находим, что \(y = \frac{180 x}{\pi}\), поэтому, используя цепное правило:

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

Итак, исходя из этого, производная синуса в градусах на самом деле равна косинусу в градусах, но умноженному на коэффициент \(\frac{180}{\pi}\).

Как найти производные в тригонометрии?

Производные триггера находятся по определению, используя основные тождества триггера. Например, с помощью синус формулы суммы мы можем вывести производную \(\sin(x)\), используя определение предела:

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

Советы и рекомендации

Главный вывод для вас — всегда напоминать, что 6 триггерных производных , и помните их наизусть, так как вы будете использовать их постоянно вместе с основными дифференцирующие правила .

Точно так же вы можете использовать тождества триггеров и определение обратной функции, чтобы найти наиболее распространенные производные обратных триггеров.

Пример: триггерный расчет производной

Рассмотрим следующую функцию: \(f(x) = \sin^2(x)+ \frac{1}{x}\). Найдите его производную

Отвечать: Производные триггера включают триггерную функцию, которую необходимо дифференцировать. Рассмотрим функцию \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\), которая содержит синусоидальную функцию, поэтому она квалифицируется как тригонометрическая производная.

Полученные Результаты : Для этого примера найдено, что производная:

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

Очень полезно изобразить функцию и ее производную на графике. См. ниже:

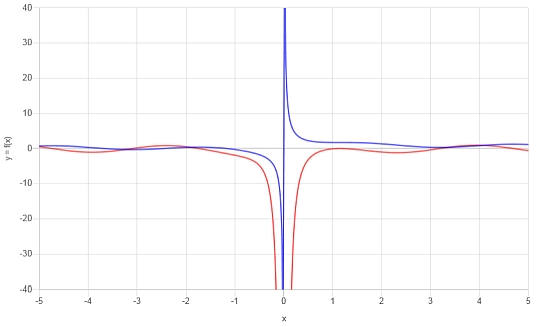
Пример производной триггерной функции

Рассмотрим следующую триггерную функцию: \(f(x) = \sin(x) + x \cos(x)\), найдите ее производную.

Отвечать: Теперь нам нужно работать с производной следующей триггерной функции \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\).

Окончательное Заключение : Мы заключаем, что производная определяется выражением:

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

Получается следующий сюжет:

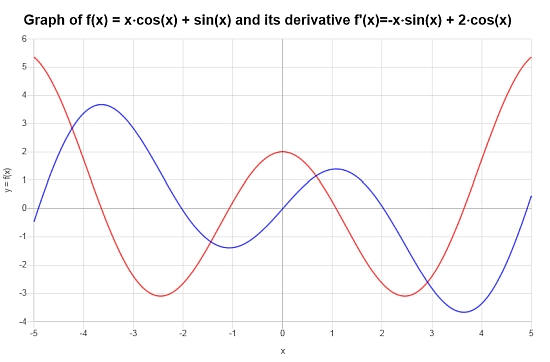
Пример: триггерные производные и неявное дифференцирование

Найдите \(\frac{dy}{dx}\) вместо \( \sin(x)+\cos(y) = 1 \).

Отвечать: Нам нужно использовать неявное дифференцирование , поэтому мы дифференцируем обе стороны и используем Правило цепи :

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

чем завершается расчет.

Другие полезные калькуляторы производных

нахождение производной простых и элементарных функций является краеугольным камнем процесса нахождения производных более сложных функций с помощью хорошо известного правила дифференциации .

В этом контексте основные Тригонометрические функции можно считать элементарными функциями, для которых производная может быть вычислена с использованием пределов, через само ее определение. Среди наиболее полезных элементарных функций у нас есть полиномы и рациональные функции.