Калькулятор периода и частоты
Инструкции: Используйте этот калькулятор периода и частоты, чтобы найти период и частоту заданной тригонометрической функции, а также амплитуду, сдвиг фазы и вертикальный сдвиг, когда это необходимо. Пожалуйста, введите периодическую функцию (Например: \(f(x) = 3\sin(\pi x)+4\))
Калькулятор периода и частоты
При работе с периодическими функциями необходимо вычислить несколько важнейших параметров, которыми являются период (\(P\)) и частота (\(f\)).
Период \(P\) периодической функции соответствует числу, удовлетворяющему следующему свойству:
\[f(x+P) = f(x)\]для всех значений \(x\). Обратите внимание, что не все функции имеют период. Те, которые имеют, называются периодические функции .
Период некоторых общих функций
Тригонометрические функции являются примерами периодических функций. Например, если мы рассмотрим функцию \(f(x) = \sin x\), ее период равен \(2\pi\), как показано на графике ниже:

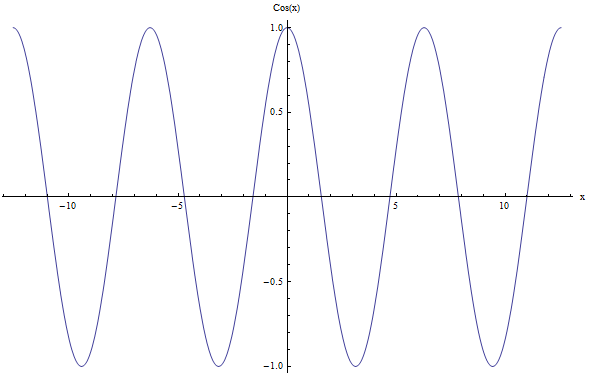
Для \(\cos x\) мы также имеем период \(2\pi\). Посмотрите на график ниже:
Период других тригонометрических функций
Вспомните, что косекант функции \(\csc x\) является обратной к \(\sin x\), это \(\csc x = \frac{1}{\sin x}\), поэтому период \(\csc x\) также равен \(2\pi\).
Аналогично, секущая функция \(\sec x\) является обратной к \(\cos x\), это \(\sec x = \frac{1}{\cos x}\), поэтому период \(\sec x\) также равен \(2\pi\).
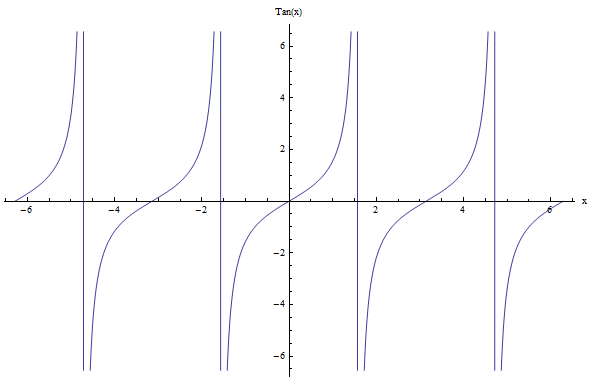
Как насчет тангенса? Функция тангенса \(\tan x\) немного отличается, потому что ее период равен \(\pi\). Действительно, ее график выглядит иначе, чем график синуса и косинуса, но тангенс также периодичен. Одно из отличий заключается в том, что \(\tan x\) имеет разрывы. Проверьте это:
Как и раньше, котангенс функции \(\cot x\) является обратной к \(\tan x\), с \(\cot x = \frac{1}{\tan x}\), поэтому период \(\cot x\) также равен \(\pi\).
Расчет частоты
Другим важным элементом, который необходимо учитывать для периодической функции, является частота (\(f\)), которая рассчитывается по периоду \(P\) как:
\[f = \frac{1}{P}\]Таким образом, частота является обратной величиной периода. И наоборот, период является обратной величиной частоты.
Например, какова частота \(\sin x\)? Следуя приведенной выше формуле, поскольку мы знаем, что для синуса период равен \(P = 2\pi\):
\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]Этот калькулятор также вычислит амплитуду, сдвиг фазы и вертикальный сдвиг, если функция определена правильно. Эти параметры в значительной степени определяют поведение тригонометрической функции.
Если вам нужно построить график тригонометрической функции, используйте следующее построитель тригонометрических графиков .






