Подробнее о полиномиальных неравенствах

Этот калькулятор может помочь вам в решении полиномиальных неравенств, показывая все этапы процесса вычисления решения, а также предоставляя вам график неравенства, изображающий решение

Предоставленное вами неравенство может быть простым, например "x^2 > 1", или более сложным, например "x^3 + 3x^2 + 3x + 1 > 0".

Как только будет предоставлено действительное полиномиальное неравенство, нажмите кнопку "Рассчитать", чтобы получить решение и все показанные шаги.

Имейте в виду, что не все предоставленные вами полиномы поддаются точным решениям. Чем ниже степень многочлена, тем больше вероятность, что будет найдено точное решение неравенства.

Что такое полиномиальное неравенство

Полиномиальное неравенство — это просто тип неравенства, в котором задействованные выражения являются полиномиальными, и ни один из его членов не является неполиномиальным выражением. Например

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

является полиномиальным неравенством, тогда как

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

нет из-за присутствия члена \(\sin x\), который не является полиномом. Решение неравенств вообще-то это сложный процесс в целом, но для полиномиальных у нас есть четкий план действий.

Как решить полиномиальное неравенство?

• Шаг 1: Убедитесь, что все члены являются полиномами. В противном случае конкретные методы, используемые для полиномов, могут быть неприменимы
• Шаг 2: Положите все на одну сторону, оставив ноль на другой стороне
• Шаг 3: Заменив знак неравенства на "=", решите соответствующее уравнение (это предполагает нахождение нулей многочлена)
• Шаг 4: Соберите все критические точки неравенства, которые в данном случае являются вещественными нулями вспомогательной Полиномиальное уравнение (в данном случае вы не учитываете комплексные корни)
• Шаг 5: Если критических точек не существует, это означает, что выражение не меняет знак, поэтому вся вещественная линия будет решением, или нет решения. Для проверки выберите любую точку и посмотрите, удовлетворяет ли она неравенству, и если да, то вся вещественная линия является решением, если нет, то решения нет
• Шаг 6: Если есть критические точки, постройте интервалы с последовательными критическими точками (используя -∞ в качестве начальной критической точки и ∞ в качестве конечной критической точки)
• Шаг 7: Проверьте каждый из этих интервалов и посмотрите, соответствует ли точка внутри неравенству. Если да, то интервал является частью решения, если нет, то интервал не является частью решения.

Ключевая идея здесь заключается в том, что критические точки и интервалы, которые мы получаем из них, являются интервалами, для которых выражение не меняет знак, поэтому либо весь интервал является решением, либо не точка в интервале является частью решения.

Полиномиальные нули и критические точки

Одна из причин, по которой решение полиномиальных неравенств возможно, заключается в том, что полиномиальные выражения относительно просто анализировать на предмет критических точек, не считая того факта, что полиномиалы являются непрерывными выражениями.

Будут неравенства типа

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

в котором будет намного сложнее найти критические точки. линейные неравенства найти критические точки еще проще, но это все. Любое общее неравенство будет представлять свои сложности.

Применение полиномов в реальной жизни

Существует множество применений полиномов. Например, в физике, когда вы изучаете кинематику, есть несколько интересных полиномиальных выражений, полученных из законов Ньютона. Эти выражения могут определять условия положения тела, что может привести к полиномиальному неравенству для определения того, в какие моменты тело находится выше определенной высоты, что может оказаться решающим, например, в баллистике.

Кроме того, при изучении дифференциальных уравнений вы можете найти в уравнении демперирующие члены, которые зависят от степени и имеют полиномиальную структуру, для чего вы можете использовать некоторые сложные неравенства, такие как неравенства Гронуолла.

Пример. решение полиномиальных неравенств

Решите: \(x^2 - x > \frac{1}{2}\)

Отвечать: Сначала нам нужно решить следующее заданное квадратное уравнение \(\displaystyle x^2-x-\frac{1}{2}=0\):

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

итак, мы выяснили, что:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Анализ критических точек

Список обнаруженных критических точек организован в порядке возрастания: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Исходя из этого, нам необходимо проанализировать следующие интервалы:

• Для интервала \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): левая часть положительна, поэтому \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) является частью решения.

• Для интервала \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): левая часть отрицательна, что означает, что \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) не является частью решения.

• Для интервала \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): левая часть положительна, что означает, что \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) является частью решения.

Решение неравенства

На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) или \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Используя интервальную запись, решение записывается как:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]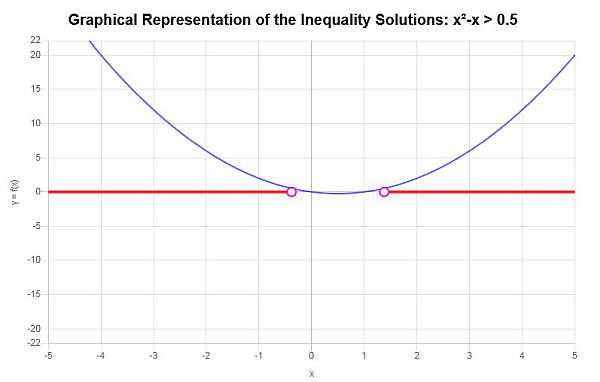

чем завершается расчет.

Пример: полином высшей степени

Решите следующее неравенство: \(x^3 - x > 1\)

Решение:

Чтобы решить \(x^3-x > 1\), мы сначала откладываем все в одну сторону:

\[x^3-x-1> 0\]

Теперь из этого мы получаем связанное уравнение, которое необходимо решить в первую очередь, а именно \(x^3-x-1=0\). Обратите внимание, что степень — \(\displaystyle deg(p) = 3\), ее старший коэффициент — \(\displaystyle a_{3} = 1\), а постоянный коэффициент — \(\displaystyle a_0 = -1\).

Попытка найти рациональные корни

Сначала мы попытаемся найти простые рациональные корни с помощью теоремы о рациональном нуле.

Следующая задача — найти целые числа, которые делят старший коэффициент \(a_{3}\) и постоянный коэффициент \(a_0\), которые будут использоваться для построения наших кандидатов как нулей полиномиального уравнения.

▹ Разделители \(a_{3} = 1\): \(\pm 1\).

▹ Разделители \(a_0 = -1\): \(\pm 1\).

Следовательно, разделив каждый делитель постоянного коэффициента \(a_0 = -1\) на каждый делитель старшего коэффициента \(a_{3} = 1\), мы находим следующий список кандидатов в корни:

\[\pm \frac{ 1}{ 1}\]

Теперь необходимо протестировать всех кандидатов, чтобы понять, являются ли они решением. В результате тестирования каждого кандидата получено следующее:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Но так как мы не нашли рациональных корней путем проверки, мы не можем продолжить факторизацию элементарными методами, поэтому процесс останавливается на этом.

НЕОБЯЗАТЕЛЬНЫЙ : Это полином степени \(3\), для которого имеется в общей сложности корни \(3\), даже если некоторые из них могут быть комплексными, но в этом случае элементарными методами было найдено менее \(3\) решений.

Используя расширенные методы кубических уравнений, можно обнаружить, что полный набор решений:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Анализ критических точек

Единственная обнаруженная критическая точка — это \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Исходя из этого, нам необходимо проанализировать следующие интервалы:

• Для интервала \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): левая часть отрицательна, поэтому \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) не является частью решения.

• Для интервала \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): левая часть положительна, что означает, что \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) является частью решения.

Решение неравенства

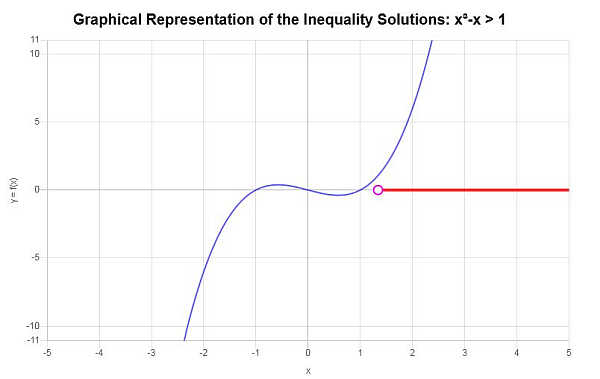
На основе предоставленного неравенства и анализа критических точек мы находим, что решение неравенства: \(x > 1.3247180451128\).

Используя интервальную запись, решение записывается как:

\[\left(1.3247180451128,\infty\right)\]

Графически:

Больше калькуляторов неравенства

Решение неравенств (запрещено поиск решений уравнений ) — одна из самых распространенных операций в математике.

Процесс решения неравенств обычно трудоемок, и вообще не существует правила их решения. Решение полиномиальных неравенств — одно из немногих исключений, в котором мы можем выполнить ряд шагов для поиска решений, но, тем не менее, мы все равно можем потерпеть неудачу, потому что с полиномами более высокой степени трудно иметь дело. Действительно, действительно невозможно найти корни многочлена выше степени 5 по общему правилу (теореме Абеля).