Дифференциальный калькулятор
Инструкции: Используйте этот дифференциальный калькулятор, чтобы найти дифференциал функции, которую вы предоставляете, в заданной точке, которую вы предоставляете, показывая все шаги. Пожалуйста, введите функцию и точку в поле формы ниже.
Дифференциальный калькулятор
Этот калькулятор позволит вам вычислить дифференциал предоставляемой вами функции в указанную вами точку, показывая все этапы процесса.
Предоставляемая вами функция может быть любой допустимой дифференцируемой функцией, такой как f(x) = x^2 + 2x или f(x) = x^2*sin(x), просто упомянем два примера.
Затем, когда вы указали функцию и точку для дифференциального расчета, просто нажмите "Рассчитать", чтобы просмотреть все этапы показанного процесса.
Идея Дифференциал находится вплотную с линией касательной и Линейное Приближение , так как дифференциал точно измеряет изменение y вдоль Касательная линия в заданной точке.
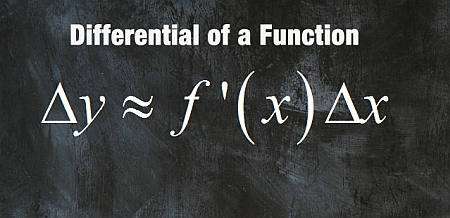
Что такое дифференциал?
В дифференциальном исчислении идея состоит в том, что производные дают вам информацию о мгновенной скорости изменения функции в данной точке.
Понятие дифференциала использует скорость изменения определяется производной в данной точке \(x_0\), чтобы аппроксимировать поведение функции ее Касательная линия .
Формула дифференциала основана на идее, что
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]где \(\Delta y = y - f(x_0)\) и \(\Delta x = x - x_0\). Для дифференциала \(dy\) определим
\[\displaystyle dy = f'(x_0) dx \]Это (расплывчатое) определение основано на идее, что линейная аппроксимация и функция приближаются к одному и тому же поведению, когда \(x\) достаточно близко к \(x_0\).
Шаги для вычисления дифференциала
- Шаг 1: Определите функцию f(x) и точку x0, в которой вы хотите вычислить дифференциал
- Шаг 2: Вычислите производную f'(x) и оцените ее в x0, чтобы получить f'(x0). Упростите его, если это необходимо
- Шаг 3: Используйте формулу \(\displaystyle dy = f'(x_0) dx \)
Иногда вы встретите дифференциал, записанный как \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), как форму указания на то, что вы будете использовать дифференциал для оценки изменений y, измеренных \(\Delta y\).
Дифференциальный калькулятор dy
Используя Дифференциальный калькулятор может сэкономить ваше время в процессе расчета производной. Идея дифференциала всегда была странной в том смысле, что она кажется нечетко определенной.
Хотя существует способ формального определения дифференциалов и их операций (предмет, называемый дифференциальными формами), большинство математиков не видят причин для существования дифференциалов, поскольку они не предоставляют никакой новой информации, которую производная или приближение первого порядка не предоставлять.
Полная дифференциальная интерпретация
Наиболее распространенное применение и интерпретация дифференциала - это использование в его "конечном" выражении:
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]где вы хотите оценить изменение y, измеренное \(\Delta y\), по изменению x, измеренному \(\Delta x\), и производной в точке.
Иногда это \(\Delta y\) называют полная вариация или же полный дифференциал .
Советы и рекомендации
Не забывайте, что дифференциал можно рассматривать как теоретическое определение \(\displaystyle dy = f'(x_0) dx \), которое указывает на бесконечно малую вариацию у, вызванную бесконечно малой вариацией х.
Его также можно использовать в его полной дифференциальной форме, в которой у вас есть
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]который сообщает вам приблизительное изменение y при изменении x (от \(x_0\) до \(x\)).
Центр всего алгебраического калькулятора начинается с мощности основных чисел дробей.
Пример: дифференциальный калькулятор
Рассмотрим функцию: \(f(x) = x^2\). Найдите его дифференциал в точке \(x_0 = 1\).
Отвечать: В случае этого первого примера мы работаем с функцией \(\displaystyle f(x)=x^2\), для которой нам нужно вычислить ее дифференциал в точке \(x_0 = 1\).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
Дифференциал : Формула для дифференциала функции \(\displaystyle f(x)=x^2\) в точке \(x_0 = 1\):
\[dy = f'(x_0)(x - x_0) \]Мы определяем \(\displaystyle y_0 = f(x_0)\), поэтому подстановка значения точки \(x_0 = 1\) в функцию приводит к:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Также подстановка значения точки \(x_0 = 1\) в вычисленную производную приводит к:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]Итак, теперь мы подставляем это значение в дифференциальную формулу, чтобы получить:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Вывод : Следовательно, мы находим, что дифференциал для функции \(\displaystyle f(x)=x^2\) в точке \(x_0 = 1\) равен:
\[dy = 2x-2 \]Пример: дифференциальный расчет
Для заданной функции: \(f(x) = x^3 + 3x^2 - 2\) найти дифференциал в точке \(x_0 = 2\).
Отвечать: Теперь нам нужно найти дифференциал для функции \(\displaystyle f(x)=x^3+3x^2-2\),
Дифференциальный Расчет : Мы используем следующую формулу для дифференциала, который нам нужно построить для данной функции \(\displaystyle f(x)=x^3+3x^2-2\), в данной точке \(x_0 = \frac{1}{2}\):
\[dy = f'(x_0)(x - x_0) \]Заметьте, что \(\displaystyle y_0 = f(x_0)\), что означает, что вычисляя функцию в \(x_0 = \frac{1}{2}\), мы находим:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Тогда получим производную в точке \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Следовательно, мы получаем следующее
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Вывод : Окончательный вывод состоит в том, что искомый дифференциал определяется выражением:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Дифференциальный пример
Нам дана функция: \(f(x) = \frac{\sin(x)}{x}\). Найдите его дифференциал в точке \(x_0 = \frac{\pi}{2}\).
Решение:
Предусмотрена следующая функция: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), для которой нужно вычислить ее дифференциал в точке \(x_0 = \frac{\pi}{2}\).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
Расчет : Теперь пришло время найти дифференциал, связанный с \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), для заданной точки \(x_0 = \frac{\pi}{2}\). Используемая формула:
\[dy = f'(x_0)(x - x_0) \]Подставляем значение точки \(x_0 = \frac{\pi}{2}\) в вычисленную производную, что приводит к:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Поэтому, используя дифференциальную формулу:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Вывод : Соответствующий дифференциал:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Другие калькуляторы дифференцирования
Поиск производных без сомнения, является ключевым элементом исчисления. Производные предоставляют информацию, необходимую для понимания скорость изменения функций. поскольку они имеют тесную связь.
К счастью, поиск деривативов — это систематический процесс (не обязательно простой), если вы будете следовать определенным правилам. правила дифференциации . Чаще всего используются правила Правило Продукта , Правило квоты и Правило цепи .
Линейный или приближения первого порядка концептуально попытаться аппроксимировать функцию линией, по крайней мере локально, и может многое рассказать о поведении функции, близкой к определенной точке.






