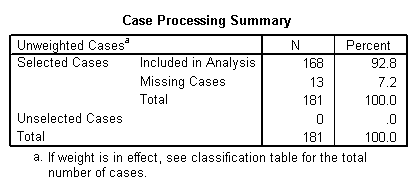
Problema: È stato fornito il seguente output che riassume i risultati di una logistica regressione intrapresa su campioni accoppiati di società quotate pubblicamente nel Regno Unito fallite e non fallite. Le variabili indipendenti impiegate sono le seguenti:

PBTCL_1 è l'utile prima delle imposte diviso per le passività correnti.

CLTA_1 rappresenta le passività correnti sul totale delle attività.

NCI_1 è l'intervallo di assenza di credito che è una misura di quanto tempo (in giorni) un'azienda può continuare a fare trading senza generare entrate.

CATL_1 è dalle attività correnti alle passività totali.

Tutti questi sono calcolati utilizzando i dati presi dagli ultimi account pubblicati prima del fallimento.

La variabile dipendente è dicotomica: alle società fallite viene assegnato 1 e alle società non fallite 0.

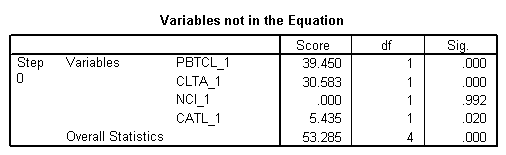
Blocco 0: blocco iniziale

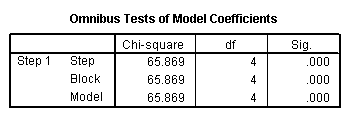
Blocco 1: Metodo = Invio

È necessario effettuare una valutazione finanziaria e statistica di queste informazioni.

Soluzione: Si osservi che il modello logistico è complessivamente significativo, p = .000. Inoltre, si è scoperto che Nagelkerke R Square = .432, che indica una bontà di adattamento relativamente accettabile per questo modello.

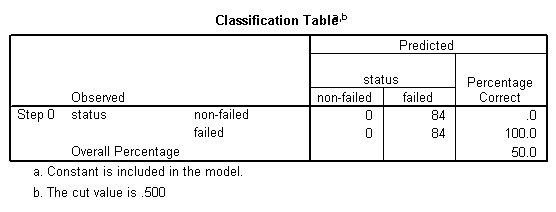
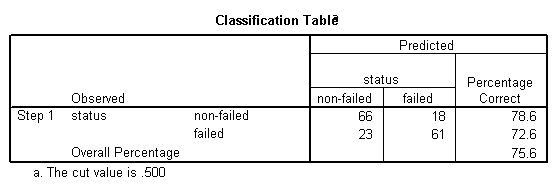
Si osserva che tra le imprese non fallite, il 78,6% è stato classificato, mentre tra le imprese fallite il 72,6% è stato classificato correttamente, che rappresenta un totale del 75,6% delle imprese complessivamente classificate correttamente, il che indica un tasso di classificazione relativamente buono.

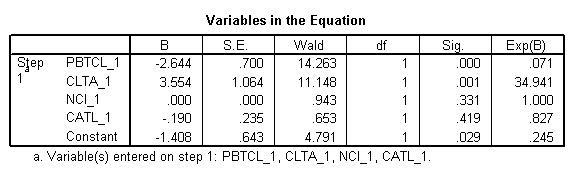
Il modello logistico è

\[\ln \left( \frac{{\hat{p}}}{1-\hat{p}} \right)=-1.408-2.644*PBTCL\_1+3.554*CLTA\_1+0.000*NCI\_1-0.190*CATL\_1\]

dove \(\hat{p}\) corrisponde alla probabilità che un'impresa fallisca. Da un punto di vista finanziario, abbiamo le seguenti conclusioni:

· Per un aumento di 1 punto dell'utile ante imposte diviso per le passività correnti, le probabilità di fallimento diminuiscono del 92,9%. Questa variazione è significativa, p = 0,000 <0,05

· Per un aumento di 1 punto delle passività correnti sul totale delle attività, le probabilità di fallimento aumentano del 3294,10% Questa variazione è significativa, p = 0,001 <0,05

· Per un aumento di un giorno nell'intervallo senza crediti, le probabilità di fallire non cambiano. Questo coefficiente non è significativo, p = 0,331> 0,05

· Per un aumento di 1 punto delle attività correnti rispetto alle passività totali, le probabilità di fallimento diminuiscono del 17,3% (questa diminuzione è significativa, p = 0,029 <0,05)