حلول حساب التفاضل والتكامل

مشتقات ثلاثية

عاليما: استخدم آلة حاسبة مشتقة ثلاثية لحساب مشتق أي وظيفة توفرها تتضمن وظائف مثلثية , مما يوضح جميع الخطوات.يرجى كتابة الوظيفة التي تريد التمييز في مربع النموذج أدناه.

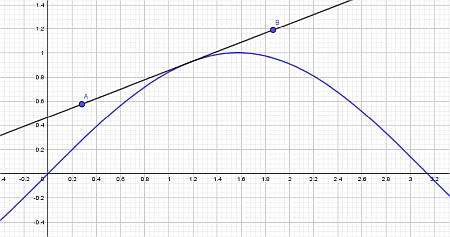
مشتقات المثلثات الأساسية

تتمثل فكرة استخدام القواعد المشتقة في تحطيم وظيفة معقدة وتمييزها باستخدام مشتقات الوظائف المعروفة.على وجه التحديد , ستلعب وظائف المثلثات البسيطة مثل الجيب وجيب التمام والظلم والكوتانغنت دورًا مهمًا في ذلك.

ما هي مشتقات المثلثات الأساسية؟

mشtق ثlaثyة 1: \(\frac{d}{dx} \sin (x) = \cos(x)\)
mشtق ثlaثyة 2: \(\frac{d}{dx} \cos (x) = -\sin(x)\)
mشtق ثlaثyة 3: \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
mشtق ثlaثy 4: \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
mشtق ثlaثyة 5: \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
MشTق Trig 6: \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

هذه هي المشتقات الأساسية التي تحتاج إلى معرفتها للغاية , وربما تحفظها من أجل الاستخدام قoaudd amشtقة لحساب مشتقات أكثر تعقيدًا

هل مشتقات ثلاثية في الدرجات؟

لا , مشتق وظائف المثلثات في راجيان , وبالتالي فإن مشتقات المثلثات وجدت تعكس حقيقة أن الحجة X تقاس في الراديان.

لذلك , على سبيل المثال , افترض أننا أردنا حساب مشتق الخطيئة في درهيت , لذلك نحدد \(f(y) = \sin(y)\) , حيث يتم قياس \(y\) بالدرجات.

الآن , دع \(x = \frac{\pi y}{180}\) زاوية مكافئة في Radians وأيضًا حل لـ \(y\) نجد أن \(y = \frac{180 x}{\pi}\) , إذن باستخدام قاعدة السلسلة:

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

بناءً على ذلك , فإن مشتق الجيب في الدرجات هو في الواقع جيب التمام في الدرجات , ولكن الأوقات عامل \(\frac{180}{\pi}\).

كيف تجد مشتقات في علم المثلثات؟

تم العثور على مشتقات TRIG بحكم التعريف , باستخدام هويات TRIG الأساسية.على سبيل المثال , باستخدام جyeb صyغة mجmou يمكننا استخلاص مشتق \(\sin(x)\) , باستخدام تعريف الحد:

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

النصائح والحيل

الوجبات الرئيسية بالنسبة لك هي أن تذكر دائمًا ما 6 mشtقat ثlaثyة وتعرف عليهم عن ظهر قلب , كما ستستخدمها بشكل مستمر , إلى جانب الأساسي tmileز alقoaud وبعد

وبالمثل , يمكنك استخدام هويات TRIG وتعريف الوظيفة العكسية للعثور على مشتقات ثلاثية العكس الأكثر شيوعًا.

مثال: حساب مشتق الثلاث

النظر في الوظيفة التالية: \(f(x) = \sin^2(x)+ \frac{1}{x}\).تجد مشتقها

الملم: المشتقات الثلاثية تنطوي على وظيفة ثلاثية تحتاج إلى التمييز.النظر في الوظيفة \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\) , والتي تحتوي على وظيفة جيبية , لذلك فهي مؤهلة كمشتق ثلاثية.

\( \displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2+\frac{1}{x}\right)\)

By using the linearity property, we know \(\frac{d}{dx}\left( \sin(x)^2+\frac{1}{x} \right) = \frac{d}{dx}\left(\sin(x)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\sin\left(x\right)^2\right)+\frac{d}{dx}\left(\frac{1}{x}\right)\)

Using the Power Rule for a polynomial term with negative exponent: \(\frac{d}{dx}\left( \frac{1}{x} \right) = -\frac{1}{x^2}\) and in this case we can use the Power Rule for a constant exponent: \(\frac{d}{dx}\left( \sin\left(x\right)^2 \right) = 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\frac{1}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cdot \cos\left(x\right)-\frac{1}{x^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle 2\sin\left(x\right)\cos\left(x\right)+\frac{-1}{x^2}\)

Directly expanding and simplifying

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\)

نتاك : على سبيل المثال , وجد أن المشتق هو:

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

من المفيد جدًا تصوير الوظيفة ومشتقها على الرسم البياني.انظر أدناه:

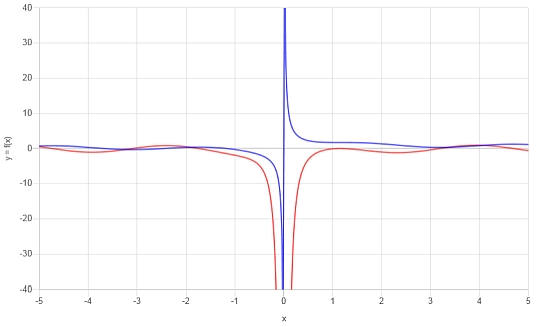
مثال على مشتق وظيفة ثلاثية

ضع في اعتبارك وظيفة TRIG التالية: \(f(x) = \sin(x) + x \cos(x)\) , ابحث عن مشتقها.

الملم: الآن , نحتاج إلى العمل مع مشتق وظيفة Trig التالية \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\).

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x\right)+\sin\left(x\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x\cos(x)+\sin(x) \right) = \frac{d}{dx}\left(x\cos(x)\right)+\frac{d}{dx}\left(\sin(x)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\cos\left(x\right)\right)+\frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\) and we can use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)+\cos\left(x\right)\)

By applying direct differentiation: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x\right)+x \left(-\sin\left(x\right)\right)+\cos\left(x\right)\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot \left(-\sin\left(x\right)\right)+\cos\left(x\right)+\cos\left(x\right)\)

We group together the terms that are multiplying \(\cos\left(x\right)\) and then simplifying \(1+1 = 2\)

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot \left(-\sin\left(x\right)\right)+2\cos\left(x\right)\)

By reorganizing the terms:

\( \displaystyle = \,\,\)

\(\displaystyle -x\sin\left(x\right)+2\cos\left(x\right)\)

الإرهاق : نستنتج أن المشتق من قبل:

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

تم الحصول على المؤامرة التالية:

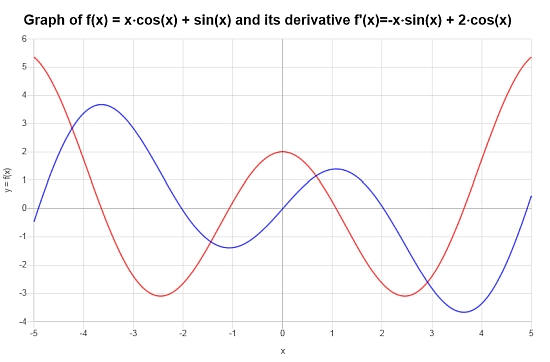
مثال: مشتقات المثلثات والتمايز الضمني

العثور على \(\frac{dy}{dx}\) لـ \( \sin(x)+\cos(y) = 1 \).

الملم: نحن بحاجة إلى استخدام العداد , لذلك نحن نميز كلا الجانبين ونستخدم قaudة السلم :

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

الذي يختتم الحساب.

الحاسبة المشتقة الأخرى المفيدة

الهاور على الله من الوظائف البسيطة والابتدائية هي حجر الزاوية في عملية العثور على مشتقات الوظائف الأكثر تعقيدًا , من خلال استخدام المعروفة جيدًا قoaud altmaiز وبعد

في هذا السياق , أساسي الداول الملمس يمكن اعتبار وظائف أولية يمكن حساب المشتق من أجلها باستخدام حدود , عبر تعريفه.من بين أكثر الوظائف الابتدائية المفيدة لدينا كثyer الدادود والوظائف العقلانية.