حلول حساب التفاضل والتكامل

حاسبة قاعدة السلسلة

عاليما: استخدم حاسبة قاعدة السلسلة هذه لحساب مشتق من أي الويسى أنت تقدم , إظهار جميع الخطوات.يرجى كتابة الوظيفة التي تريد تطبيق قاعدة السلسلة في مربع النموذج أدناه.

حول قاعدة السلسلة

ستسمح لك هذه الآلة الحاسبة بتطبيق قاعدة السلسلة على أي وظيفة مركبة تقدمها.أ الويسى يتوافق مع الحالة عند تقييم وظيفة داخل وظيفة ما.من أجل عمل حاسبة قاعدة السلسلة , تحتاج إلى توفير وظيفة مركبة صالحة وقابلة للتمييز.

أحد الأمثلة على وظيفة صالحة سيكون f (x) = (sin (x))^2 , حيث لدينا هنا وظيفة 'x^2' التي يتم تقييمها في وظيفة أخرى , وهي SIN (x) , تشكيل أالوظيفة المركبة.

بمجرد توفير وظيفة صالحة وقابلة للتمييز , فإن الشيء التالي الذي عليك فعله هو النقر على الزر الذي يقرأ "حساب" , والذي سيقوم بعد ذلك بتعيين الحسابات في الحركة وسيتم عرض جميع الخطوات.

مشتق قاعدة السلسلة هو واحد من قاعدة التمايز الأكثر استخدامًا.وذلك لأن تكوين الوظيفة هو أحد أكثر الطرق الطبيعية لبناء وظائف جديدة على أساس الوظائف الابتدائية.

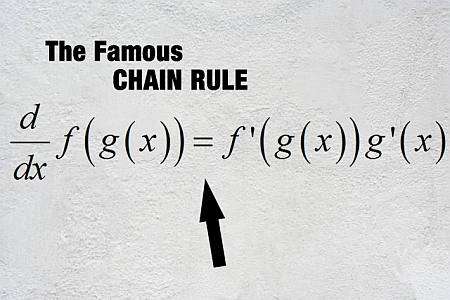
ما هي قاعدة السلسلة

بالكلمات البسيطة , تسمح قاعدة السلسلة بتمييز الوظائف المركبة , فهذه هي الوظائف التي يتم تقييمها داخل وظائف أخرى.لذلك , لنفترض أن لدينا الوظيفة \(f(x)\) و \(g(x)\) , ونحن نعرف كيفية حساب مشتق هذه الوظائف , والتي هي \(f'(x)\) و \(g'(x)\).

ثم , هناك أ صyغة قaudة السلم يتيح لنا ذلك حساب مشتق الدالة المركب \(f \circ g\) , والذي يتم تعريفه على أنه \((f \circ g)(x) = f(g(x))\):

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

خطوات لاستخدام قاعدة السلسلة

الظهر 1: حدد الوظيفة الخارجية f (x) والوظيفة الداخلية g (x)
ال alخطoة 2: تأكد من أن f (x) و g (x) هي وظائف صالحة , قابلة للتمييز , وحساب المشتقات المقابلة f '(x) و g' (x)
الله 3: استخدم الصيغة (f \ circ g) '(x) = f' (g (x)) g '(x) , مما يشير إلى أننا نقيم مشتق الوظيفة الخارجية في الوظيفة الداخلية , وضرب ذلك بواسطة المشتقمن الوظيفة الداخلية

لاحظ كيف تستخدم الخطوات أعلاه فكرة الوظيفة "الداخلية" و "الخارجية".ربما لا يكون هذا مصطلحًا قياسيًا , بل فكرة يمكن أن تساعدك في تحديد الدور الذي تلعبه كل وظيفة عند استخدام قاعدة السلسلة.

تطبيقات قاعدة السلسلة

قاعدة السلسلة هي في الواقع أداة ممتازة للعثور على المشتقات , وعادة ما سيكون مفتاح أي حaSbة mشtقة , جنبا إلى جنب مع كل الأساسيات الأخرى قoaudd amشtقة .لكن قاعدة السلسلة لها تفسير خاص في ما يسمى مدى ميرتبطة

لإعطاء سياق لفكرة الأسعار ذات الصلة , لنبدأ بشيء من كتابة قاعدة السلسلة التي ربما يجد الكثير من الناس فهم: أسهل:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

يقول الشكل أعلاه لقاعدة السلسلة أنه إذا كنت \(y\) وظيفة \(z\)وظيفة \(x\) , ويمكنك العثور على مشتق \(y\) فيما يتعلق \(x\) باستخدام قاعدة السلسلة.

كما كنت قد تشتبه , يلعب \(y\) دور \(f(x)\) (الوظيفة "الخارجية") و \(z\) يلعب دور \(g(x)\) (الدالة "الداخلية").

يربط الشكل أعلاه لقاعدة السلسلة معدل تغيير Y فيما يتعلق بـ X , مع معدلات تغيير Y فيما يتعلق بـ z و z فيما يتعلق بـ X , وبالتالي مصطلح "المعدلات ذات الصلة".

هذا مفيد للغاية في الممارسة العملية.مثال: يزداد نصف قطر الدائرة بمعدل 2 سم/ثانية , ما هو معدل تغيير مساحة الدائرة؟لذلك , يمكنك إما الذهاب والتعبير عن نصف قطر الدائرة كدالة لـ T , مما يعكس حقيقة أنه يزداد بمعدل 2 سم/ثانية , أو يمكنك استخدام قاعدة السلسلة.

لذلك يمكنك تسمية المنطقة , ص نصف قطرها , والوقت.ما تحتاج إلى حسابه هو \(\displaystyle \frac{dA}{dt}\) , لذلك يمكنك استخدام قاعدة السلسلة مباشرة , لأنك تعرف \(A = \pi r^2\) , و r '(t) = 2 , إذن

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

قاعدة سلسلة المشتقات الجزئية

هل يمكنك استخدام قاعدة السلسلة مع الملمس ؟بطبيعة الحال , فإن التمايز الجزئي يشبه تمامًا التمايز المنتظم , إلا أنه من المفترض أن تكون المتغيرات الأخرى ثابتة , لذا فإن المعتاد قoaudd amشtقة يتقدم.

إذن , ينطبق المثل الأعلى لقاعدة السلسلة متعددة المتغيرات , فقط أن متغير واحد يختلف في وقت واحد.

تكامل قاعدة السلسلة

قاعدة السلسلة بمعنى ما لا ينطبق كأداة مشتقة , ولكن بدلاً من ذلك تصبح أداة تكامل لا تقدر بثمن للبدائل وتغيير المتغيرات.

يمكن تصوره كنوع من قاعدة السلسلة العكسية من نوع ما.

مثال: استخدام قاعدة السلسلة

احسب مشتق الوظيفة: \(f(x) = \sin(\cos(x)) \)

الملم: النظر في الوظيفة \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\).تتوافق هذه الوظيفة مع تكوين وظيفتين: SIN (X) و COS (X) , ولأسباب ستطبق قاعدة السلسلة في هذه الحالة.

\( \displaystyle \frac{d}{dx}\left(\sin\left(\cos\left(x\right)\right)\right)\)

So we start using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(\cos\left(x\right)\right) \right) = \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

Next, directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right) \cos\left(\cos\left(x\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right)\cos\left(\cos\left(x\right)\right)\)

Finally, the following is found

\( \displaystyle = \,\,\)

\(\displaystyle \left(-1\right)\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\)

ما هاو الطراحة : يمكننا أن نستنتج أن المشتق الذي نبحث عنه هو:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

وهذا يختتم الحساب.

مثال قاعدة السلسلة

باستخدام قاعدة السلسلة , وأي قواعد مشتقة أخرى , احسب: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

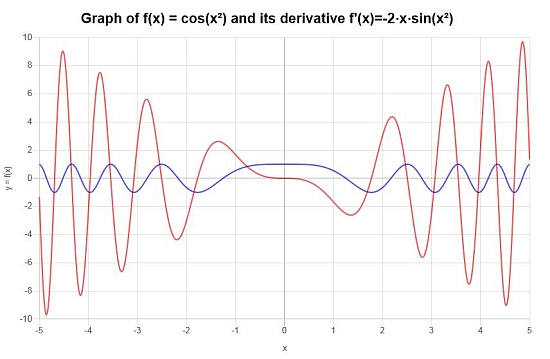
الملم: في هذا المثال , لدينا الوظيفة \(\displaystyle f(x)=\cos\left(x^2\right)\) , والتي تتوافق مع وظيفة مركبة , والتي تشير إلى أن قاعدة السلسلة هي القاعدة المشتقة الصحيحة للبدء (ستكون هناك حاجة إلى قواعد أخرى على طول الحسابات)

\( \displaystyle \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

أولاً , نستخدم قاعدة السلسلة: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

يمكننا استخدام قاعدة الطاقة للمصطلحات متعدد الحدود في هذه الحالة: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \left(-\sin\left(x^2\right)\right)\)

ثم نجد

\( \displaystyle = \,\,\)

\(\displaystyle 2x\cdot \left(-\sin\left(x^2\right)\right)\)

الآن , ببساطة إعادة تنظيم المصطلحات

\( \displaystyle = \,\,\)

\(\displaystyle -2x\sin\left(x^2\right)\)

الله : chittntaz ho أn mmشtق hloظiفة chomقadmة ytm ttقdimh bboasطة:

\[f'(x) = -2x\sin\left(x^2\right)\]

ymكnna bnaء altصoyer alrastomy altaly ablى alفaصl chyza \([-5, 5]\):

Mثal: حstab قaudة سالسال

حstab mشtق \( f(x) = x^2 \sin(x^2)\) bastخadam قaudة السلم.

المحلول:

twفyer chaloظyفة hltalyة: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\) , walty nحtaج إlى حSAB mشtقha.

جaءt hloظiفة mebsطةbalفupl , حtى ntmكn mn jnmtaBafة mebazerة llحatsab mشtقha:

\( \displaystyle \frac{d}{dx}\left(x^2\sin\left(x^2\right)\right)\)

يمكننا استخدام قاعدة المنتج: \(\frac{d}{dx}\left( x^2\sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

باستخدام قاعدة السلسلة: \(\frac{d}{dx}\left( \sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \cos\left(x^2\right)\) واستخدام قاعدة القوة للمصطلحات متعددة الحدود: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \sin\left(x^2\right)+x^2 \cdot 2x\cdot \cos\left(x^2\right)\)

إذن نحصل على ذلك

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

تجميع الأعداد الصحيحة وتجميع المصطلحات مع \(x\) في المصطلح \(x^2\cdot 2x\cos\left(x^2\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

إذن نحصل

\( \displaystyle = \,\,\)

\(\displaystyle 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\)

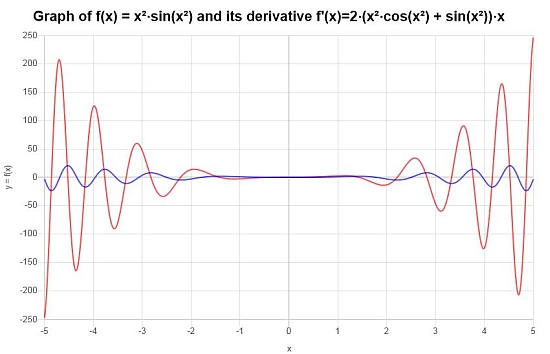
ما هاو الدة : chittntaج hlnehaئy ho أn klmشtق alذy nbحث uneh iubطى: