المحللين حساب التفاضل والتكامل

حاسبة التقريب الخطي

عاليمت: استخدم هذه الآلة الحاسبة لحساب التقريب الخطي لوظيفة معينة في نقطة معينة تقدمها , مما يوضح جميع الخطوات.يرجى كتابة الوظيفة والنقطة في مربع النموذج أدناه.

حاسبة التقريب الخطي

هذا حASBة alخطiة سيسمح بحساب التقريب الخطي , المعروف أيضًا باسم خط alظl لأي وظيفة صالحة معينة , عند نقطة صالحة معينة.

تحتاج إلى توفير وظيفة صالحة مثل F (x) = x*sin (x) , أو f (x) = x^2 - 2x + 1 , أو أي وظيفة صالحة يمكن تفكيكها , ونقطة \(x_0\)حيث يتم تعريف الوظيفة بشكل جيد.يمكن أن تكون هذه النقطة أي تعبير رقمي صالح , مثل 1/3 , على سبيل المثال.

بمجرد تقديم وظيفة ونقطة صالحة , يمكنك النقر فوق "حساب" وسيتم عرض جميع الحسابات لك.

ابحث عن التقريب الخطي أو الأول عن تقريب الوظيفة المحددة بواسطة خط , عند نقطة معينة \(x_0\).بطبيعة الحال بالنسبة للمنحنيات , سيكون التقريب الخطي خشنًا , على الرغم من أن الفكرة الرئيسية هي أن التقريب سيكون دقيقًا للنقاط القريبة من \(x_0\).

تقريب خطي

الفكرة هي العثور على خط يمر عبر نقطة \((x_0, f(x_0))\)و "بالكاد يلمس" الوظيفة \(f(x)\).يتم تقديم التعريف الرياضي الرسمي لـ "اللمس بالكاد" من خلال فكرة خط alظl , والتي نحتاج إليها حSAB الجهادية من الوظيفة.

في الواقع , تعتمد صيغة التقريب الخطي عند النقطة \(x_0\)على المشتق \(f'(x_0)\), على النحو التالي

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

هذا صyغة hltقrafyb alخطy يحدد بشكل أساسي ماعد الله يمر هذا النقطة \((x_0, f(x_0))\), ولهذا السبب يسمى "التقريب الخطي" , لأنه يحدد وظيفة خطية تتزامن مع \(f(x)\)في النقطة \(x_0\), وهي قريبة جدًا من \(f(x)\)للقيم\(x\)التي تقترب من\(x_0\).

خطوات لإيجاد التقريب الخطي

الظهر 1: تحتاج إلى الحصول على وظيفة معينة f (x) والنقطة x0.يجب أن تكون الوظيفة قابلة للتمييز في x0
ال alخطoة 2: حساب F (x0) و f '(x0) , والتي هي وظيفة ومشتق الوظيفة f في النقطة x0
الله 3: حدد التقريب الخطي كـ y = f (x_0) + f '(x_0) (x - x_0) , وهي صيغة الخطية المقدمة أعلاه

يمثل هذا الخط , \(y = f(x_0) + f'(x_0) (x - x_0)\) التقريب الأول , المعروف أيضًا باسم التقريب الخطي المحلي.

رابط مع خط الظل

كما كنت قد اشتبهت الآن , فإن التقريب الخطي هو نفسه خط alظl عند نقطة معينة.ثم , فإن حساب التقريب الخطي هو بالضبط نفس حساب خط الظل

اسم آخر لنفسه هو تقريب من الدرجة الأولى , أو تقريب خط الظل , والتي هي أسماء شائعة الاستخدام في حساب التفاضل والتكامل أيضًا.

التقريب التفاضلي والخطي

مفهوم شائع آخر هو مفهوم الفرق , والذي يرتبط ارتباطًا وثيقًا بمفهوم التقريب الخطي , وهو مجرد اشتقاق منه.في الواقع , يتم تعريف التفاضل (أو الاختلاف المحدود) على أنه \(\Delta y = y - f(x_0)\).إذن , استنادًا إلى صيغة التقريب من الدرجة الأولى , تكون صيغة التفاضلية

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

يبدو هذا بشكل طبيعي تمامًا مثل صيغة التقريب الخطي , باستثناء أن مصطلح \(f(x_0\) يتم تمريره إلى اليسار.

مثال: حساب التقريب من الدرجة الأولى.

ضع في اعتبارك ما يلي: \(f(x) = x^2 - 2x + 3\), ابحث عن تقديره الأول في \(x_0 = 1\).

إل: الوظيفة التي تم توفيرها هي \(\displaystyle f(x)=x^2-2x+3\), ونحن بحاجة إلى العثور على التقريب الخطي حول النقطة x = 1. إذن , نحتاج أولاً إلى المشتق.

\( \displaystyle \frac{d}{dx}\left(x^2-2x+3\right)\)

By linearity: \(\frac{d}{dx}\left( x^2-2x+3 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)\)

Directly: \(\frac{d}{dx}\left( 2x \right) = 2\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2\)

طريف : معادلة التقريب الخطي الذي نبحث عنه في النقطة \(x_0 = 2\) يتم تقديمه بواسطة الصيغة التالية

\[y = y_0 + f'(x_0)(x - x_0) \]

لاحظ أنه بحكم التعريف \(\displaystyle y_0 = f(x_0)\), مما يعني أننا نحتاج إلى توصيل الوظيفة في النقطة \(x_0 = 2\):

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

نحن نفعل نفس الشيء , ولكن الآن للمشتق عند النقطة \(x_0 = 2\), إذن

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

الآن مع هذا , نعود إلى صيغة التقريب الخطي:

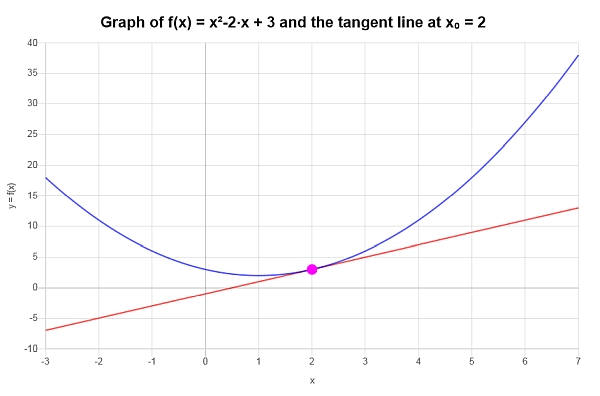
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

خatmة : نستنتج أن التقريب الخطي لـ \(\displaystyle f(x)=x^2-2x+3\) في \(x_0 = 2\) يتم تقديمه بواسطة:

\[y = 2x-1 \]

بيانياً:

مثال: المزيد من التقريب من الدرجة الأولى

للدالة: \(f(x) = x \sin(x)\)والنقطة \(x_0 = 2\), ابحث عن تقريب الترتيب الأول المقابل.

إل: في هذه الحالة , فإن الوظيفة التي نحتاج إلى عملها هي: \(\displaystyle f(x)=x\sin\left(x\right)\).

نحن الآن نحسب مشتقها:

\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)

Using the Product Rule: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)

Finally, simplifying

\( \displaystyle = \,\,\)

\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)

طريف : معادلة التقريب الخطي هي:

\[y = y_0 + f'(x_0)(x - x_0) \]

حيث \(\displaystyle y_0 = f(x_0)\), إذن نحسب:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

للمشتق في \(x_0 = 2\) نجد ذلك:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

نحن الآن مستعدون لإعادة هذه الصيغة التقريبية من الدرجة الأولى:

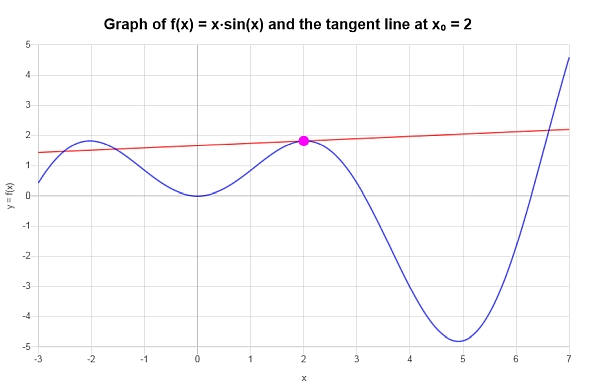
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

خatmة : لقد استنتج أن التقريب الخطي لـ \(\displaystyle f(x)=x\sin\left(x\right)\) في نقطة معينة \(x_0 = 2\) يتم حسابها على النحو التالي:

\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

بيانياً , نحصل على المؤامرة التالية:

مثال: حساب التقريب الخطي

احسب تقريب الترتيب الأول لـ \( f(x) = \frac{\sin(x)}{x}\)في \(x = \frac{\pi}{4}\).

إل: تم توفير الوظيفة التالية: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), والتي نحتاج إلى حساب مشتقها.

جاءت الوظيفة مبسطة بالفعل , حتى نتمكن من المتابعة مباشرة لحساب مشتقها:

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}\)

Therefore, we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}\)

طريف مان الهاول : المعادلة لتقريب الترتيب الأول المقابل للدالة المحددة \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) في نقطة معينة \(x_0 = \frac{\pi}{4}\) يتم تقديمها بما يلي:

\[y = y_0 + f'(x_0)(x - x_0) \]

توصيل القيم المقابلة:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

حتى الآن يمكننا وضع هذا في الصيغة:

\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

خatmة : يمكننا أن نستنتج بالتالي أن التقريب الأول للوظيفة المحددة \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) في نقطة معينة

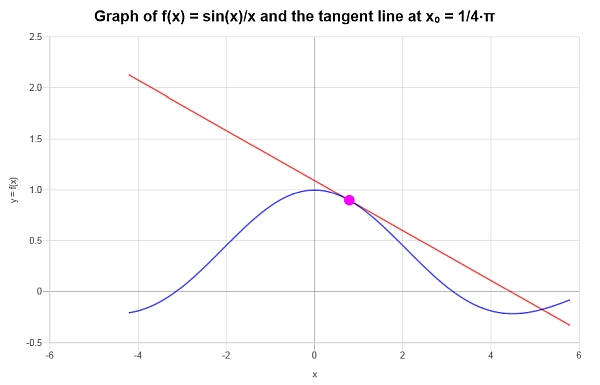
\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

يتم الحصول على ما يلي بيانياً: