حلول حساب التفاضل والتكامل

الآلة الحاسبة التفاضلية

عاليما: استخدم هذه الآلة الحاسبة التفاضلية , لإيجاد الفرق في الوظيفة التي تقدمها , عند نقطة معينة تقدمها , مع إظهار جميع الخطوات.يرجى كتابة الوظيفة والنقطة في مربع النموذج أدناه.

الآلة الحاسبة التفاضلية

ستسمح لك هذه الآلة الحاسبة بحساب الفرق في الوظيفة التي تقدمها , عند نقطة توفرها , والتي تُظهر جميع خطوات العملية.

يمكن أن تكون الوظيفة التي تقدمها أي وظيفة قابلة للتمييز صالحة مثل f (x) = x^2 + 2x , أو f (x) = x^2*sin (x) , فقط لذكر مثالين.

بعد ذلك , عندما تكون قد قدمت الوظيفة ونقطة الحساب التفاضلي , فقط انقر فوق "حساب" حتى للحصول على جميع خطوات العملية المعروضة.

فكرة آلتاكليه بإحكام مع خط الظل و طريف , نظرًا لأن الفرق هو قياس تباين Y بدقة خط alظl عند نقطة معينة.

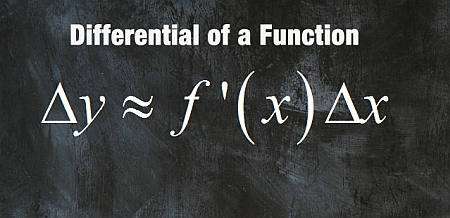
ما هو التفاضل؟

في حساب التفاضل والتكامل التفاضلي , تتمثل الفكرة في أن المشتقات تمنحك معلومات حول معدل تغيير الدالة الفوري في نقطة معينة.

مفهوم الاستخدامات التفاضلية مدال آلتوير تحددها المشتق في نقطة معينة \(x_0\) لتقريب سلوك الوظيفة بواسطة خط alظl وبعد

تعتمد صيغة الفرق على فكرة أن

\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]

حيث \(\Delta y = y - f(x_0)\) و \(\Delta x = x - x_0\).للتفاضلية \(dy\) , نحددها

\[\displaystyle dy = f'(x_0) dx \]

يعتمد هذا التعريف (الفضفاض) على فكرة أن التقريب الخطي ونهج الوظيفة لنفس السلوك عندما يكون \(x\) قريبًا بما فيه الكفاية من \(x_0\).

خطوات لحساب التفاضل

الظهر 1: حدد الوظيفة F (x) والنقطة X0 التي تريد حساب الفرق فيها
ال alخطoة 2: حساب المشتق F '(x) وقم بتقييمه في x0 , بحيث تحصل على f' (x0).تبسيطه , إذا لزم الأمر
الله 3: استخدم الصيغة \(\displaystyle dy = f'(x_0) dx \)

في بعض الأحيان , ستجد التفاضل المكتوب على أنه \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \) , كشكل من أشكال الإشارة إلى أنك ستستخدم التفاضل لتقدير التغيرات في Y , تقاس بواسطة \(\Delta y\).

الآلة الحاسبة التفاضلية dy

باستخدام alآlة alحastopة hltفazalyة يمكن أن يوفر لك الوقت مع عملية حساب المشتق.لطالما كانت فكرة التفاضلية غريبة , بمعنى أنه يبدو أنه محدد بشكل فضفاض.

على الرغم من أن هناك طريقة لتحديد الفروق وعملياتها رسميًا (موضوع يسمى الأشكال التفاضلية) , فإن معظم علماء الرياضيات لا يرون سببًا لوجود الفرق , لأنهم لا يوفرون أي معلومات جديدةلا تقدم.

التفسير التفاضلي الكلي

التطبيق الأكثر شيوعًا وتفسير الفرق هو عند استخدامه في تعبيره "المحدود":

\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]

حيث تتطلع إلى تقدير التباين في Y , كما تم قياسه بواسطة \(\Delta y\) , من التباين في x , كما تم قياسه بواسطة \(\Delta x\) والمشتق عند هذه النقطة.

في بعض الأحيان , يطلق على هذا \(\Delta y\) آثبايين الليم أو altفazaliة وبعد

النصائح والحيل

لا تنسى أن التفاضل يمكن اعتباره كتعريف نظري , \(\displaystyle dy = f'(x_0) dx \) , مما يشير إلى التباين اللانهائي في y بسبب تباين غير محدود في x.

كما يمكن استخدامه في شكله التفاضلي الكلي , الذي لديك

\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]

الذي يخبرك بتغير تقريبي في Y , عندما يكون التغيير في X (من \(x_0\) إلى \(x\)).

يبدأ مركز جميع الآلة الحاسبة الجبرية بقوة الأعداد الأساسية للكسور.

مثال: الآلة الحاسبة التفاضلية

النظر في الوظيفة: \(f(x) = x^2\).ابحث عن التفاضل عند النقطة \(x_0 = 1\).

الملم: في حالة هذا المثال الأول , نعمل مع الوظيفة \(\displaystyle f(x)=x^2\) , والتي نحتاج إلى حساب الفرق في النقطة \(x_0 = 1\).

جاءت الوظيفة مبسطة بالفعل , حتى نتمكن من المتابعة مباشرة لحساب مشتقها:

\( \displaystyle \frac{d}{dx}\left(x^2\right)\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x\)

آلتاكليه : صيغة التفاضلية للدالة \(\displaystyle f(x)=x^2\) عند النقطة \(x_0 = 1\) هي:

\[dy = f'(x_0)(x - x_0) \]

نحدد \(\displaystyle y_0 = f(x_0)\) , ثم توصيل قيمة النقطة \(x_0 = 1\) في الدالة يؤدي إلى:

\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]

أيضا , توصيل قيمة النقطة \(x_0 = 1\) في المشتق المحسوب يؤدي إلى:

\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]

إذن , نقوم الآن بتوصيل هذه القيمة في الصيغة التفاضلية للحصول على:

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]

تاسنتا : لذلك , نجد أن التفاضل للوظيفة \(\displaystyle f(x)=x^2\) عند النقطة \(x_0 = 1\) هو:

\[dy = 2x-2 \]

مثال: الحساب التفاضلي

للوظيفة المحددة: \(f(x) = x^3 + 3x^2 - 2\) , ابحث عن التفاضل عند النقطة \(x_0 = 2\).

الملم: الآن , الوظيفة التي نحتاجها لإيجاد الفرق بين \(\displaystyle f(x)=x^3+3x^2-2\) ,

\( \displaystyle \frac{d}{dx}\left(x^3+3x^2-2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3+3x^2-2 \right) = \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2\right)\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)+3 \cdot \frac{d}{dx}\left(x^2\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+3 \cdot 2x\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+3\cdot 2x\)

We reduce the integers that can be multiplied: \(\displaystyle 3\times2 = 6\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2+6x\)

Directly reorganizing/simplifying/expanding

\( \displaystyle = \,\,\)

\(\displaystyle 3\left(x+2\right)x\)

الإسبح : نحن نستخدم الصيغة التالية للفرق التي نحتاجها إلى إنشاء الوظيفة المحددة \(\displaystyle f(x)=x^3+3x^2-2\) , في النقطة المحددة \(x_0 = \frac{1}{2}\) هي:

\[dy = f'(x_0)(x - x_0) \]

لاحظ أن \(\displaystyle y_0 = f(x_0)\) , مما يعني أن تقييم الوظيفة في \(x_0 = \frac{1}{2}\) نجد:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]

ثم , نحصل على المشتق عند النقطة \(x_0 = \frac{1}{2}\):

\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]

وبالتالي , نحصل على ما يلي

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]

تاسنتا : الاستنتاج النهائي هو أن التفاضل الذي نبحث عنه يعطى:

\[dy = \frac{15}{4}x-\frac{15}{8} \]

مثال تفاضلي

لقد أعطينا الوظيفة: \(f(x) = \frac{\sin(x)}{x}\).ابحث عن التفاضل عند النقطة \(x_0 = \frac{\pi}{2}\).

المحلول:

تم توفير الوظيفة التالية: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) , والتي نحتاج إليها لحساب التفاضل في النقطة \(x_0 = \frac{\pi}{2}\).

جاءت الوظيفة مبسطة بالفعل , حتى نتمكن من المتابعة مباشرة لحساب مشتقها:

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}\)

So then after simplifying:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}\)

ايسامبي : حان الوقت الآن للعثور على الفرق المرتبط بـ \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) , للنقطة المعطاة \(x_0 = \frac{\pi}{2}\).الصيغة المستخدمة هي:

\[dy = f'(x_0)(x - x_0) \]

نقوم بتوصيل قيمة النقطة \(x_0 = \frac{\pi}{2}\) في المشتق المحسوب , مما يؤدي إلى:

\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]

لذلك , باستخدام الصيغة التفاضلية:

\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

تاسنتا : الفرق المقابل هو:

\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]

الحاسبة التمييز الأخرى

العرف هو بدون سؤال عنصر أساسي في حساب التفاضل والتكامل.توفر المشتقات المعلومات المطلوبة لفهم مدال آلتوير من الوظائف.لأن هؤلاء لديهم اتصال حميم.

لحسن الحظ , يعد العثور على المشتقات عملية منهجية (ليست سهلة بالضرورة) إذا اتبعت محددة قoaud altmaiز .القواعد الأكثر استخدامًا هي سيدا ب قaudة alحaصl و قaudة السلم وبعد

خطي أو آتورب مان الهاول حاول من الناحية النظرية تقريب وظيفة بخط , على الأقل محليًا , ويمكن أن تخبرك كثيرًا عن سلوك الوظيفة , بالقرب من نقطة معينة.