The Quadratic Formula: How to Solve a Quadratic Equation?

The quadratic equation is one of the most popular and broadly equations in Math. In terms of its definition, the quadratic equation is an equation of the form:

\[a x^2 + b x + c = 0\]

where \(a\), \(b\) and \(c\) are constants, with \( a \ne 0\). This is the way a quadratic equation is defined, where its leading term \(a\) must be different from zero.

Good news is that the above equation is really not too hard to solve, which is great considering that the quadratic equation appears literally everywhere in Algebra, Calculus and pretty much everywhere in Math and Science topics.

The Quadratic Equation Solution

Now, the question is how to solve this quadratic equation formulated above. Fortunately, the answer simple and well-known: The quadratic equation gets its solutions using the following quadratic formula

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

The values obtained with this equation are known as the roots of the quadratic equation (also known as solutions of the equation). In order to analyze the nature of the solution, the discriminant is defined as:

\[D = b^2 - 4ac\]

Types of Solutions to the Quadratic Formula

Based on the value of the discriminant, the nature of the solutions is defined. In fact, when \(D \ge 0\), then there are two different real solutions, when \(D = 0\), there is one repeated real solution, and when \(D \le 0\), there are two different imaginary solutions. This quadratic equation solver helps you make these calculations automatically.

This can be summarized as follows:

• For \(b^2 - 4ac > 0\): The equation has two real roots
• For \(b^2 - 4ac = 0\): The equation has one (repeated) real root
• For \(b^2 - 4ac < 0\): The equation has two complexl roots

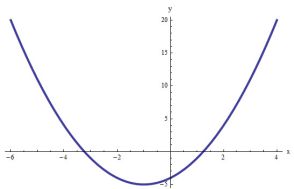
One of the neat things of this quadratic equation solver is that it will show the steps to compute the y-intercept, the coordinates of the vertex and it will plot the quadratic function

.

Quadratic Formula Steps

There are several steps you have to follow in order to successfully solve a quadratic equation:

Step 1: Identify the coefficients. Examine the given equation of the form \(ax^2+bx+c\), and determine the coefficients \(a\), \(b\) and \(c\). The coefficient \(a\) is the coefficient that appears multiplying the quadratic term \(x^2\).

The coefficient \(b\) is the coefficient that appears multiplying the linear term \(x\), and the coefficient \(c\) is the constant.

Example: Suppose that you have the following expression: \(x^2+3x+1\). What are the coefficients? In this case \(a = 1\) (the coefficient multiplying the quadratic term \(x^2\)), \(b = 3\) (the coefficient multiplying the linear term \(x\)), and \(c = 1\) (the constant).

Example: How about Suppose that you have the following expression: \(\frac{5}{4} + \frac{3}{4} x + \frac{1}{2} x^2\). What are the coefficients now? In this case \(a = \frac{1}{2}\) (the coefficient multiplying the quadratic term \(x^2\)), \(b = \frac{3}{4}\) (the coefficient multiplying the linear term \(x\)), and \(c = \frac{5}{4}\) (the constant).

Example: What happens with following expression: \(-3 + \frac{1}{2} x\). In this case, we have that \(a = 0\), because the expression does not contain a quadratic term \(x^2\), so in this case, this is not a quadratic expression.

Step 2: Plug the coefficients you found in the formula. The formula is quadratic formula is

\[x = \displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

so you need to replace the value of the coefficients \(a\), \(b\) and \(c\).

Example: If you have the equation: \(-3x^2 + 2x-1 = 0\), you find that \(a = -3\), \(b = 2\) and \(c = -1\). So, plugging this values in the formula we get:

\[x = \displaystyle\frac{-2 \pm \sqrt{2^2 - 4(-3)(-1)}}{2(-3)}\]

Step 3: Simplify the values in the equation, once you have plugged the values of \(a\), \(b\) and \(c\) . In the previous example, we would have

\[x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}\]

Step 4: Look inside of the square root. If the value is positive, then the quadratic equation has two real roots. If the value is 0, then there is one real root, and if the value inside of the square root is negative, then there are two complex root. In the previous example, we have a -8 inside of the square root, so we have two complex solutions, as shown below:

\[x = \displaystyle\frac{-2 \pm \sqrt{4 - 12}}{-6} = \frac{-2 \pm \sqrt{-8}}{-6}= \frac{-2 \pm i \sqrt{8}}{-6}\]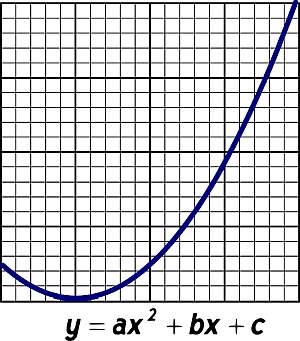

What is the Quadratic formula Used For

The quadratic formula is one of the most ubiquitous formula in mathematics. It appears when you are solving all kind of geometric problems, such as when you are maximizing an area, given a fixed perimeter, or in numerous word problems.

Lots of people wonder if there is any relationship between this quadratic equation formula and the method of completing the square . The answer is simple: you arrive the quadratic formula by solving the quadratic equation via completing the square. It is exactly the same idea, that derives to the quadratic formula that we all know.

Observe that the solutions to the quadratic equation have a very interesting geometric property: when you compute the average of the solutions found, you get the x-coordinate of the vertex of the parabola, which helps you find the vertex form of a parabola, also known as the standard form, used in many applications, form example with conical sections.

Quadratic Formula Examples

Compute the roots of the following quadratic equation: \(3x^2 - 2x + 4 = 0\)

Solution:

The following equation needs to be solved:

\[ 3 x^2 -2 x + 4 = 0\]

This corresponds to a quadratic equation. The following formula is used to find the solutions:

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

Using the above formula, we get that:

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-2) \pm \sqrt{ (-2)^2 - 4(3)(4)}}{2(3)}\]\[= \frac{ 2 \pm \sqrt{ -44}}{ 6}\]

Hence, the solutions are:

\[x_1 = 0.333 - 1.106 i \] \[x_2 = 0.333 + 1.106 i \]

Therefore, there are two imaginary solutions \(x_1 = 0.333 - 1.106 i \) and \(x_2 = 0.333 + 1.106 i \).

Also, the y-intercept occurs at \(y = 4\), which means that the coordinates of the y-intercept are \((0, 4)\).

Finally, the coordinates of the vertex are:

\[x_V = \frac{-b}{2a} = \frac{-(-2)}{2\cdot 3} = 0.3333\] \[y_V = f(x_V) = 3 (0.3333)^2 -2 (0.3333) + 4 = 3.6667\]