More About this Geometric Mean Calculator

First of all, the geometric mean is a measure of central tendency, but it is a type of a less commonly used measure of central tendency, much less common than the sample mean or the median .

How do you calculate the geometric mean?

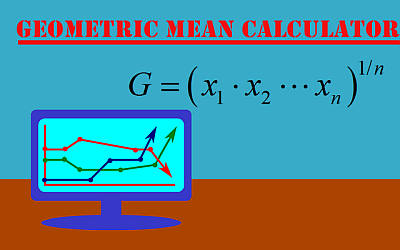
The geometric mean, also known as geometric average is somewhat more cumbersome to calculate than it is to calculate the arithmetic mean. Mathematically, in terms of its calculation, and the formula used to calculate it, it is computed by using the following geometric mean formula

$$G = \left( x_1 \cdot x_2 \cdot \cdot \cdot x_n \right)^{1/n}$$

In general, for the sample $\{x_1, x_2, ..., x_n\}$, the arithmetic mean is larger than the geometric mean.

So, how to find geometric mean? Simply you multiply the n terms in the sample and apply the n-th root to that product. Simple.

Applications of the Geometric Mean

There are different types of applications in which the geometric mean is the appropriate measure of center, or some other cases where the harmonic mean is the appropriate measure of center.

Still, by far, in the majority of applications, the arithmetic mean is the one that is used as measure of center, although is not unusual to find special situations.

But yet, despite the popularity of the arithmetic mean, there will be situations where you will want to find the geometric mean, or another suitable measure of central tendency, to meet the specific characteristics of the data you are working with.

Do you need to calculate the mean anyway?

Yes, it is convenient for you to use this mean calculator to get the sample mean, as well as the median and the mode, along with the harmonic mean, so to have a complete picture of all the available measures of central tendency.