समाधानकर्ताओं गणना

व्युत्पन्न कैलकुलेटर

सराय: आपके द्वारा प्रदान किए गए किसी फ़ंक्शन के व्युत्पन्न को खोजने के लिए इस व्युत्पन्न कैलकुलेटर का उपयोग करें, प्रक्रिया के सभी चरणों को दिखाते हुए।कृपया उस फ़ंक्शन को टाइप करें जिसे आप नीचे दिए गए बॉक्स में व्युत्पन्न की गणना करना चाहते हैं।

व्युत्पन्न कैलकुलेटर

यह व्युत्पन्न कैलकुलेटर आपको किसी दिए गए फ़ंक्शन के व्युत्पन्न को खोजने के लिए उपयोग किए जाने वाले सभी चरणों और नियमों के माध्यम से ले जाएगा।आपको 3x + sin (x^2) जैसे फ़ंक्शन में टाइप करना होगा, या आप वास्तव में इसे पूरे फ़ंक्शन परिभाषा के साथ प्रस्तावित कर सकते हैं, जैसे f (x) = 3x^2 + 2Tan (x^3)।

ध्यान दें कि इसे पहले व्युत्पन्न कैलकुलेटर के रूप में संदर्भित किया जा सकता है, जो एक व्युत्पन्न कैलकुलेटर के समान है।पहले व्युत्पन्न और व्युत्पन्न एक ही चीज़ का प्रतिनिधित्व करते हैं, और "पहले" भाग को आमतौर पर गिरा दिया जाता है।

प्रदान किया गया फ़ंक्शन पूरी तरह से सरल हो सकता है या नहीं, यह कोई फर्क नहीं पड़ता, क्योंकि कैलकुलेटर पहले फ़ंक्शन को सरल करेगा यदि आवश्यक हो तो इसके व्युत्पन्न की गणना करने से पहले आवश्यक हो।

एक बार तमाम प्रदान किया गया है, आपको बस "गणना" पर क्लिक करने की आवश्यकता है, कुछ सेकंड प्रतीक्षा करें, और गणना के सभी चरण आपको प्रस्तुत किए जाएंगे।

भेदभाव कैलकुलस (एकीकरण के साथ) में उपयोग किया जाने वाला मुख्य उपकरण है और यह एक महत्वपूर्ण ऑपरेशन है जो मोटे तौर पर अधिक उन्नत गणित में उपयोग किया जाता है।कुछ बहुत ही सामान्य अनुप्रयोगों में शामिल हैं अफ़संद , मैक्सिमा और मिनीमा और बहुत कुछ।

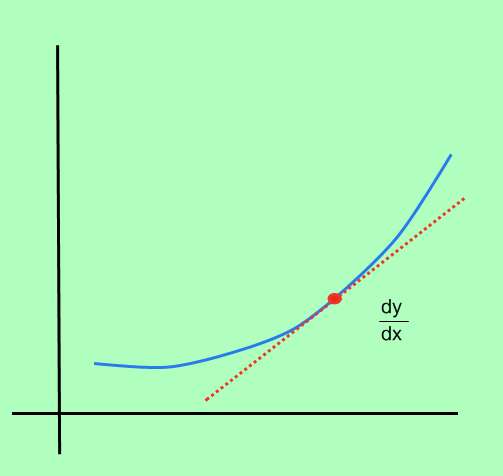
किसी फ़ंक्शन के व्युत्पन्न की गणना कैसे करें?

किसी फ़ंक्शन के व्युत्पन्न की गणना करने की प्रक्रिया को कहा जाता है तमाम , और इसमें फ़ंक्शन के डोमेन में प्रत्येक बिंदु पर, बिंदु के परिवर्तन की तत्काल दर का निर्धारण करना शामिल है।

किसी फ़ंक्शन के परिवर्तन की त्वरित दर क्या है?ठीक है, चलो की परिभाषा के साथ शुरू करते हैं सराफक : एक फ़ंक्शन \(f\)पर विचार करें, और मान लें कि हमारे पास दो अंक हैं, \(x_0\)और \(x_1\)।बिंदु \(x_0\)पर, फ़ंक्शन \(f(x_0)\)है, और बिंदु \(x_1\)पर, फ़ंक्शन मान \(f(x_1)\)लेता है

फिर, F में परिवर्तन को \(\Delta y = f(x_1) - f(x_0)\) के रूप में परिभाषित किया गया है (जिसे y में परिवर्तन के रूप में भी जाना जाता है)।इसके अलावा, X में परिवर्तन को \(\Delta x = x_1 - x_0)\)के रूप में परिभाषित किया गया है।सरल शब्दों में, \(\Delta x\) x में परिवर्तन है, जबकि \(\Delta y\) फ़ंक्शन के मूल्य में परिवर्तन है, x में परिवर्तन के कारण।

रेखांकन:

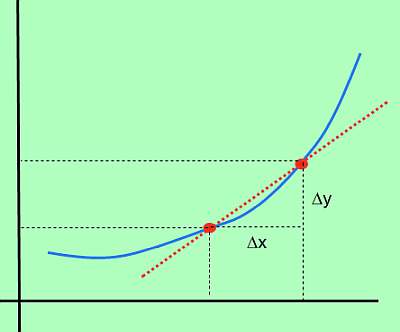
व्युत्पन्न सूत्र

तो, यदि\(\Delta x\) x में परिवर्तन का प्रतिनिधित्व करता है, और\(\Delta y\) फ़ंक्शन के मूल्य में परिवर्तन का प्रतिनिधित्व करता है, तो x में परिवर्तन के कारण, इसी सराफक है:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

तो फिर, परिवर्तन की त्वरित दर क्या होगी?यह विश्लेषण करने से मेल खाती है कि अगर \(\Delta x\) वास्तव में छोटा हो जाता है तो क्या होगा।एक उम्मीद करेगा कि \(\Delta y\)भी छोटा हो जाएगा, लेकिन यह \(\Delta y\)और \(\Delta x\)के बीच की दर के लिए होगा?

तो, इस संदर्भ में, परिवर्तन की त्वरित दर को परिभाषित किया गया है

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

इसलिए, आम आदमी के शब्दों में, हम \(x_0\)फिक्स्ड सेट करते हैं और हम \(x_1\)के मूल्यों के लिए परिवर्तन की दर की गणना करते हैं जो \(x_0\)के करीब और करीब हैं।परिवर्तन की त्वरित दर के इस विचार का उपयोग करते हुए, हम एक बिंदु \(x_0\)पर व्युत्पन्न के लिए निम्न सूत्र दे सकते हैं।

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

यदि उपरोक्त सीमा बाहर निकलती है, तो हम कहते हैं कि फ़ंक्शन f \(x_0\)पर भिन्न है।इसके अलावा, हम कहेंगे कि एक फ़ंक्शन एक सेट ए पर अलग है, यदि फ़ंक्शन सेट के प्रत्येक बिंदु पर अलग -अलग है।

व्युत्पन्न सूत्र का उपयोग करने के लिए कदम

Letsunt 1: स्पष्ट रूप से उस फ़ंक्शन को पहचानें जिसे आप अंतर करना चाहते हैं
Their दो दो: सुनिश्चित करें कि आप जितना संभव हो सके एफ को सरल बनाएं, अन्यथा आवश्यक सीमा को खोजना अनावश्यक रूप से कठिन हो सकता है
Theirण 3: तय करें कि आप एक सामान्य बिंदु X0 के साथ काम करेंगे, या आप X0 के लिए एक विशिष्ट संख्यात्मक बिंदु दे रहे हैं
च ४: ४: फ़ंक्शन की परिभाषा के आधार पर, फॉर्मूला \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \)का उपयोग करें।यह है, f में X0 और X1 के मानों को प्लग करें, और देखें कि सूत्र कैसे बीजगणितीय रूप से दिखता है
च ५: ५: सीमा लेने से पहले जितना हो सके उतना सरल करें
च viry: 6: कभी -कभी X1 = x0 + h सेट करना आसान होता है, और फिर सीमा की गणना के रूप में H को 0 में परिवर्तित किया जाता है

ध्यान दें कि चरण 6 एक है जो कुछ लोग डिफ़ॉल्ट के रूप में पसंद करते हैं।वास्तव में, वैकल्पिक व्युत्पन्न सूत्र जो सरलीकरण उद्देश्यों के लिए आसान लग सकता है:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

कौन सा सूत्र है जो आपको अपनी पाठ्यपुस्तक में अन्य के बजाय मिल सकता है।

व्युत्पन्न नियम

यह सूत्र का उपयोग करके व्युत्पन्न की गणना करने के लिए बहुत सारे काम की तरह लगेगा।और वास्तव में, यह एक श्रमसाध्य प्रक्रिया हो सकती है यदि हमने व्युत्पन्न सूत्र का उपयोग करके हर भेदभाव प्रक्रिया को पूरा करने का फैसला किया।

सौभाग्य से, कई कार्य हैं (अर्थात्) तंग , अफ़्री ) जिसके लिए हम सटीकता के साथ जानते हैं कि उनके व्युत्पन्न क्या हैं।

उसके ऊपर, हमारे पास है विभेदन नियम यह हमें एक फ़ंक्शन के व्युत्पन्न को खोजने की अनुमति देता है जो एक है अफ़्री और/या प्राथमिक कार्यों का एक संयोजन (जिसके लिए हम उनके व्युत्पन्न को जानते हैं), प्राथमिक डेरिवेटिव के संदर्भ में।

व्युत्पन्न की गणना के लिए क्या कदम हैं?

Letsunt 1: फ़ंक्शन f की पहचान करें जिसे आप अंतर करना चाहते हैं।इसके व्युत्पन्न की गणना करने से पहले जितना हो सके उतना सरल करें
Their दो दो: यह निर्धारित करें कि आपको व्युत्पन्न सूत्र का उपयोग करने के लिए आवश्यक है या नहीं
Theirण 3: यदि आपको व्युत्पन्न सूत्र का उपयोग करना है, तो \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \)का उपयोग करें, या आप \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \)का उपयोग कर सकते हैं यदि यह आसान लगता है
च ४: ४: यदि आपको व्युत्पन्न सूत्र का उपयोग करने की आवश्यकता नहीं है, तो आप मुख्य भेदभाव नियमों का उपयोग कर सकते हैं: रैखिकता, पmurauguth नियम , तंग और तिहाई , जो आपको बुनियादी ज्ञात डेरिवेटिव का उपयोग करने के लिए व्युत्पन्न की गणना को कम करने में मदद करेगा

अक्सर बार, जिस कार्य को आप करने की कोशिश कर रहे हैं तमाम के लिए एक साधारण कार्य नहीं है, लेकिन यह कई सरल कार्यों का बुनियादी संयोजन है।उदाहरण के लिए, फ़ंक्शन

\[f(x) = x + \cos(x) + \sin(x)\]

अपने आप में एक प्राथमिक कार्य नहीं है, लेकिन यह है अफ़्री तीन प्राथमिक कार्यों में से, \(x\), \(\sin x\)और \(\cos x\)।

डेरिवेटिव के आवेदन

कोई सोच सकता है "ठीक है, डेरिवेटिव में सीमाएं शामिल हैं और यह सुपर सैद्धांतिक है, इसलिए इसके लिए बहुत अधिक अनुप्रयोग नहीं होने चाहिए", लेकिन आप पूरी तरह से गलत होंगे।डेरिवेटिव का जादू यह है कि वे अनिवार्य रूप से कार्यों के परिवर्तन की दर के बारे में हैं, जो विभिन्न प्रकार की प्रक्रियाओं का प्रतिनिधित्व कर सकते हैं।

यही कारण है कि भेदभाव परिवर्तन की प्रक्रिया का अध्ययन करने की अनुमति देता है, और बदलते चर की तुलना कैसे करें, जिसमें एक व्यापक प्रयोज्यता है।

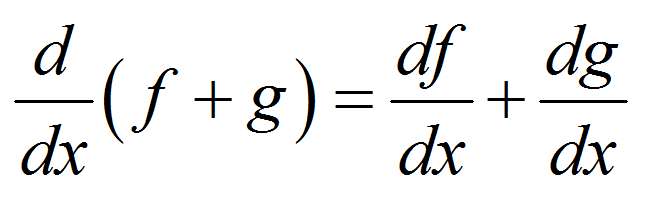
उदाहरण: व्युत्पन्न की गणना

\(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)के लिए x के संबंध में व्युत्पन्न की गणना करें

तमाम: निम्नलिखित फ़ंक्शन प्रदान किया गया है: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), जिसके लिए हमें इसके व्युत्पन्न की गणना करने की आवश्यकता है।

पraurauraurauray: इस मामले में, हमें पहले दिए गए फ़ंक्शन \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \)को सरल बनाने की आवश्यकता है, और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरणों का संचालन करते हैं:

\( \displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\)

Directly reorganizing/simplifying/expanding

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\)

फ़ंक्शन को सरल बनाने के बाद, हम व्युत्पन्न की गणना के लिए आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( \frac{1}{3}x+\frac{5}{4}\cos(x)-\frac{5}{4}\sin(x^2) \right) = \frac{d}{dx}\left(\frac{1}{3}x\right)+\frac{5}{4} \cdot \frac{d}{dx}\left(\cos(x)\right)-\frac{5}{4}\cdot \frac{d}{dx}\left(\sin(x^2)\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\frac{1}{3}x\right)+\frac{5}{4} \cdot \frac{d}{dx}\left(\cos\left(x\right)\right)-\frac{5}{4}\cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \cos\left(x^2\right)\),directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\) and directly we get: \(\frac{d}{dx}\left( \frac{1}{3}x \right) = \frac{1}{3}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4} \left(-\sin\left(x\right)\right)-\frac{5}{4}\cdot \frac{d}{dx}\left(x^2\right)\cdot \cos\left(x^2\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4} \left(-\sin\left(x\right)\right)-\frac{5}{4}\cdot 2x\cdot \cos\left(x^2\right)\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}\cdot \left(-\sin\left(x\right)\right)-\frac{5}{4}\cdot 2x\cos\left(x^2\right)\)

Grouping and operating all the integer terms and fractions: \(\displaystyle 2 \times \left(-\frac{ 5}{ 4}\right)=-\frac{ 5}{ \cancel{ 2} \times 2} \times \cancel{ 2}=-\frac{ 5}{ 2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}\cdot \left(-\sin\left(x\right)\right)-\frac{5}{2}x\cos\left(x^2\right)\)

Directly reorganizing/simplifying/expanding

\( \displaystyle = \,\,\)

\(\displaystyle -\frac{5}{2}x\cos\left(x^2\right)-\frac{5}{4}\sin\left(x\right)+\frac{1}{3}\)

निम्नलिखित प्लॉट \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\)के लिए अंतराल \([-5, 5]\)के लिए प्राप्त किया गया है:

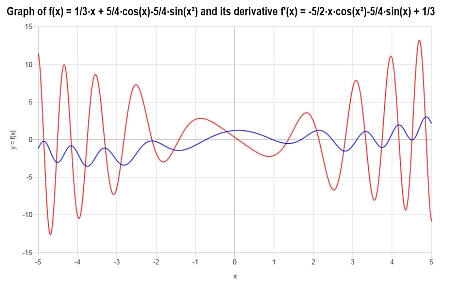
उदाहरण: एक फ़ंक्शन को अलग करना

Calculate the derivative of : \(f(x) = \sin(\cos(x^2))\), and provide the graph of \(f(x)\) and \(f'(x)\).

तमाम: अब हमारे पास \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\)है।

The function came already simplified, so we can proceed directly to compute its derivative. By using this derivative cal we get:

\( \displaystyle \frac{d}{dx}\left(\sin\left(\cos\left(x^2\right)\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(\cos\left(x^2\right)\right) \right) = \frac{d}{dx}\left(\cos\left(x^2\right)\right)\cdot \cos\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\cos\left(x^2\right)\right)\cdot \cos\left(\cos\left(x^2\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(\frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\right) \cos\left(\cos\left(x^2\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\cdot \left(-\sin\left(x^2\right)\right)\right) \cos\left(\cos\left(x^2\right)\right)\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle 2x\cdot \left(-\sin\left(x^2\right)\right)\cos\left(\cos\left(x^2\right)\right)\)

Expanding and simplifying the expression

\( \displaystyle = \,\,\)

\(\displaystyle -2x\cos\left(\cos\left(x^2\right)\right)\sin\left(x^2\right)\)

इसलिए, हम अंतराल \([-5, 5]\)पर फ़ंक्शन के लिए निम्नलिखित प्लॉट प्राप्त करते हैं:

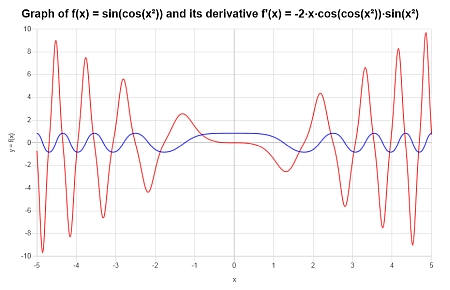
उदाहरण: व्युत्पन्न कैलकुलेटर

\( f(x) = \displaystyle \frac{4}{x}\)का व्युत्पन्न खोजें।क्या यह हर जगह अच्छी तरह से परिभाषित है?इसे ग्राफ़ करें।

तमाम: वह कार्य जिसके लिए व्युत्पन्न की आवश्यकता होती है, \(\displaystyle f(x)=\frac{4}{x}\)है।

आगे कोई सरलीकरण की आवश्यकता नहीं है, इसलिए हम इसके व्युत्पन्न की गणना करने के लिए सीधे आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(\frac{4}{x}\right)\)

Using the Power Rule for a polynomial term with negative exponent: \(\frac{d}{dx}\left( \frac{4}{x} \right) = -\frac{4}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle -\frac{4}{x^2}\)

रेखांकन:

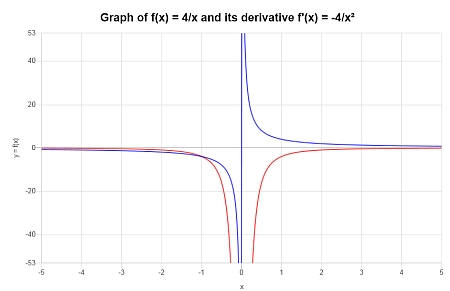
डेरिवेटिव और कार्यों के बारे में अधिक

यह Rayrणों के kana व व rayr आपके लिए बहुत उपयोगी साबित होगा क्योंकि यह किसी भी दिए गए फ़ंक्शन के व्युत्पन्न की गणना का संचालन करेगा, प्रक्रिया के सभी चरणों को दिखाते हुए, उपयुक्त को लागू करेगा वmuntumam नियम , और आपको बता रहे हैं कि उन्हें कब लागू किया जा रहा है और क्यों।

इस कैलकुलेटर को भी कहा जा सकता है तंग या तंग जैसा कि यह ठीक है कि यह क्या करता है, यह DY/DX अनुपात की सीमा की गणना करता है क्योंकि DX 0 तक पहुंचता है।

गणित में कार्य बेहद महत्वपूर्ण निर्माण हैं।भेदभाव के साथ, आपको सक्षम होने की आवश्यकता है अफ़सू आमतौर पर, अन्य अधिक विशिष्ट गणनाओं की प्रस्तावना के रूप में।ऐसे विशेष प्रकार के कार्य हैं जो आपको विशिष्ट संचालन करने की अनुमति देते हैं, जैसे कि आप क्या करते हैं अँगुला ।

दिलचस्प बात यह है कि बहुत सारे महत्वपूर्ण तत्व जैसे निर्देशांक खोजते हैं अफ़र्याश यह ज्यामितीय तर्कों का उपयोग करके एक चतुर तरीके से प्राप्त किया जा सकता है, भेदभाव का उपयोग करके तुच्छ रूप से प्राप्त किया जा सकता है।

इसके अलावा, का विचार तमाम और तमाम स्वाभाविक रूप से दिखाई दें, व्युत्पन्न की अवधारणा से बाहर, और एक प्राकृतिक विस्तार।