समाधानकर्ताओं गणना

रैखिक सन्निकटन कैलकुलेटर

सराय: किसी दिए गए बिंदु पर दिए गए फ़ंक्शन के लिए रैखिक सन्निकटन की गणना करने के लिए इस कैलकुलेटर का उपयोग करें, जो आपके द्वारा दिए गए सभी चरणों को दिखाते हैं।कृपया फ़ंक्शन और नीचे दिए गए फॉर्म बॉक्स में बिंदु टाइप करें।

रैखिक सन्निकटन कैलकुलेटर

यह रत्न रैखिक सन्निकटन की गणना करने की अनुमति देगा, जिसे भी जाना जाता है तमाम किसी भी मान्य फ़ंक्शन के लिए, किसी दिए गए वैध बिंदु पर।

आपको उदाहरण के लिए f (x) = x*sin (x), या f (x) = x^2 - 2x + 1, या किसी भी मान्य फ़ंक्शन की तरह एक मान्य फ़ंक्शन प्रदान करने की आवश्यकता है, जो कि अलग -अलग है, और एक बिंदु \(x_0\)जहां फ़ंक्शन अच्छी तरह से परिभाषित है।यह बिंदु उदाहरण के लिए, 1/3 की तरह कोई भी मान्य संख्यात्मक अभिव्यक्ति हो सकता है।

एक बार जब आप एक वैध फ़ंक्शन और बिंदु प्रदान करते हैं, तो आप "गणना" पर क्लिक करते हैं और सभी गणना आपके लिए दिखाई जाएंगी।

किसी दिए गए बिंदु \(x_0\)पर एक पंक्ति द्वारा दिए गए फ़ंक्शन के एक अनुमान के लिए रैखिक या प्रथम क्रम सन्निकटन देखें।स्वाभाविक रूप से घटता के लिए एक रैखिक सन्निकटन मोटा होगा, हालांकि मुख्य विचार यह है कि सन्निकटन \(x_0\)के करीब बिंदुओं के लिए सटीक होगा।

रेखीय सन्निकटन

विचार एक पंक्ति को खोजने के लिए है जो बिंदु \((x_0, f(x_0))\)से होकर गुजरता है और यह "बमुश्किल छूता है" फ़ंक्शन \(f(x)\)।'मुश्किल से छूने' की औपचारिक गणितीय परिभाषा के विचार से दी गई है तमाम , जिसके लिए हमें जरूरत है वthaumaun की की kayrें फ़ंक्शन का।

वास्तव में, बिंदु \(x_0\)पर रैखिक सन्निकटन के लिए सूत्र व्युत्पन्न \(f'(x_0)\)पर निर्भर करता है, इस प्रकार है

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

यह रोटी अनिवार्य रूप से परिभाषित करता है एक पंक्ति का समीकरण यह बिंदु \((x_0, f(x_0))\)से होकर गुजरता है, यही कारण है कि "रैखिक सन्निकटन" कहा जाता है, क्योंकि यह एक रैखिक फ़ंक्शन को परिभाषित करता है जो \(f(x)\)के साथ संयोग करता है \(x_0\)पर, और यह मानों के मानों के लिए \(f(x)\)के बहुत करीब है\(x\)जो\(x_0\)के करीब हैं।

रैखिक सन्निकटन को खोजने के लिए कदम

Letsunt 1: आपको एक दिए गए फ़ंक्शन f (x) और एक बिंदु X0 की आवश्यकता है।फ़ंक्शन X0 पर भिन्न होना चाहिए
Their दो दो: गणना f (x0) और f '(x0), जो फ़ंक्शन और व्युत्पन्न फ़ंक्शन के फ़ंक्शन X0 पर f हैं
Theirण 3: रैखिक सन्निकटन को y = f (x_0) + f '(x_0) (x - x_0) के रूप में परिभाषित करें, जो ऊपर प्रस्तुत रैखिककरण सूत्र है

This line, \(y = f(x_0) + f'(x_0) (x - x_0)\) represents the first order approximation, also known as local linear approximation.

स्पर्शरेखा रेखा के साथ लिंक

जैसा कि आपको शायद अब तक संदेह है, रैखिक सन्निकटन समान है तमाम दिए गए बिंदु पर।फिर, रैखिक सन्निकटन की गणना बिल्कुल समान है जैसे कि स्पर्शरेखा रेखा की गणना

उसी के लिए एक और नाम पहले ऑर्डर सन्निकटन, या स्पर्शरेखा रेखा सन्निकटन है, जो आमतौर पर कैलकुलस में भी उपयोग किए जाते हैं।

विभेदक और रैखिक सन्निकटन

एक और सामान्य अवधारणा अंतर की है, जो कसकर रैखिक सन्निकटन से जुड़ी हुई है, और यह बस इसकी व्युत्पत्ति है।वास्तव में, अंतर (या परिमित अंतर) को \(\Delta y = y - f(x_0)\)के रूप में परिभाषित किया गया है।तो, पहले आदेश सन्निकटन सूत्र के आधार पर, अंतर के लिए सूत्र है

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

यह स्वाभाविक रूप से रैखिक सन्निकटन फॉर्मूला की तरह दिखता है, सिवाय इसके कि \(f(x_0\) शब्द बाईं ओर पारित किया गया है।

उदाहरण: पहले आदेश सन्निकटन की गणना।

निम्नलिखित पर विचार करें: \(f(x) = x^2 - 2x + 3\), \(x_0 = 1\)पर इसका पहला ऑर्डर सन्निकटन खोजें।

तमाम: जो फ़ंक्शन प्रदान किया गया है वह \(\displaystyle f(x)=x^2-2x+3\)है, और हमें बिंदु x = 1 के आसपास रैखिक सन्निकटन को खोजने की आवश्यकता है। इसलिए, हमें पहले व्युत्पन्न की आवश्यकता है।

\( \displaystyle \frac{d}{dx}\left(x^2-2x+3\right)\)

By linearity: \(\frac{d}{dx}\left( x^2-2x+3 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)\)

Directly: \(\frac{d}{dx}\left( 2x \right) = 2\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2\)

रोटी : रैखिक सन्निकटन के लिए समीकरण जिसे हम बिंदु \(x_0 = 2\) की तलाश कर रहे हैं, निम्न सूत्र द्वारा दिया गया है

\[y = y_0 + f'(x_0)(x - x_0) \]

ध्यान दें कि परिभाषा \(\displaystyle y_0 = f(x_0)\), जिसका अर्थ है कि हमें फ़ंक्शन को बिंदु \(x_0 = 2\)पर प्लग करने की आवश्यकता है:

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

हम भी ऐसा ही करते हैं, लेकिन अब बिंदु \(x_0 = 2\)पर व्युत्पन्न के लिए, तो

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

अब इसके साथ, हम रैखिक सन्निकटन सूत्र पर वापस आते हैं:

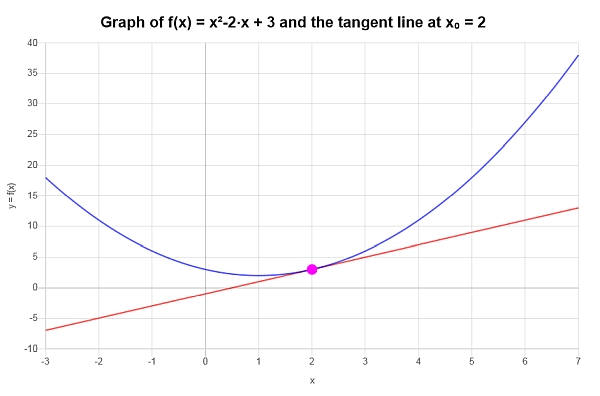
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

तिहाई : हम निष्कर्ष निकालते हैं कि \(\displaystyle f(x)=x^2-2x+3\) पर \(x_0 = 2\) के लिए रैखिक सन्निकटन द्वारा दिया गया है:

\[y = 2x-1 \]

रेखांकन:

उदाहरण: अधिक पहला आदेश सन्निकटन

फ़ंक्शन के लिए: \(f(x) = x \sin(x)\)और बिंदु \(x_0 = 2\), इसी पहले ऑर्डर सन्निकटन को खोजें।

तमाम: इस मामले में, हमें जिस कार्य को काम करने की आवश्यकता है, वह है: \(\displaystyle f(x)=x\sin\left(x\right)\)।

अब हम इसके व्युत्पन्न की गणना करते हैं:

\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)

Using the Product Rule: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)

Finally, simplifying

\( \displaystyle = \,\,\)

\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)

रोटी : रैखिक सन्निकटन का समीकरण है:

\[y = y_0 + f'(x_0)(x - x_0) \]

जहां \(\displaystyle y_0 = f(x_0)\), तो हम गणना करते हैं:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

\(x_0 = 2\) पर व्युत्पन्न के लिए हम पाते हैं:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

अब हम इन्हें पहले ऑर्डर सन्निकटन फॉर्मूले में वापस रखने के लिए तैयार हैं:

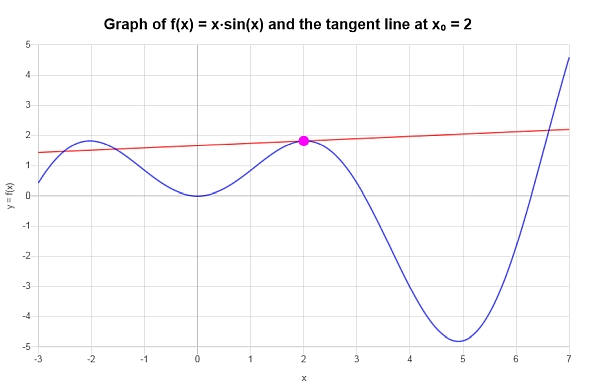
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

तिहाई : यह निष्कर्ष निकाला गया है कि दिए गए बिंदु पर \(\displaystyle f(x)=x\sin\left(x\right)\) का रैखिक सन्निकटन \(x_0 = 2\) के रूप में गणना की जाती है:

\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

ग्राफिक रूप से, हमें निम्नलिखित प्लॉट मिलता है:

उदाहरण: रैखिक सन्निकटन गणना

\( f(x) = \frac{\sin(x)}{x}\)पर \( f(x) = \frac{\sin(x)}{x}\)के लिए पहले ऑर्डर सन्निकटन की गणना करें।

तमाम: निम्नलिखित फ़ंक्शन प्रदान किया गया है: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), जिसके लिए हमें इसके व्युत्पन्न की गणना करने की आवश्यकता है।

फ़ंक्शन पहले से ही सरल हो गया, इसलिए हम सीधे इसके व्युत्पन्न की गणना करने के लिए आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}\)

Therefore, we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}\)

तमाम : दिए गए फ़ंक्शन \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) के लिए दिए गए फ़ंक्शन \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) के लिए पहले ऑर्डर सन्निकटन के लिए समीकरण \(x_0 = \frac{\pi}{4}\) निम्नलिखित द्वारा दिया गया है:

\[y = y_0 + f'(x_0)(x - x_0) \]

संबंधित मानों को प्लग करना:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

तो अब हम इसे सूत्र में डाल सकते हैं:

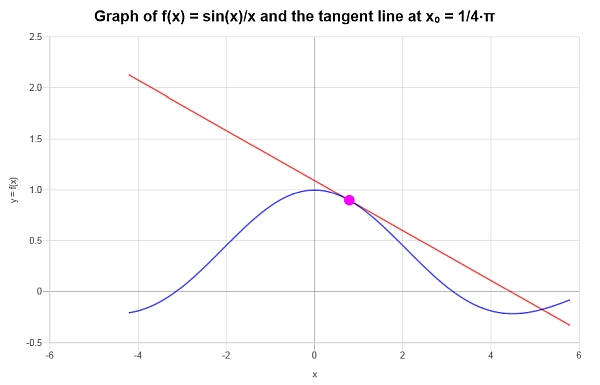
\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

तिहाई : हम इसलिए निष्कर्ष निकाल सकते हैं कि दिए गए फ़ंक्शन \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) के लिए पहला ऑर्डर सन्निकटन दिया गया है \(x_0 = \frac{\pi}{4}\) द्वारा दिया गया है

\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

निम्नलिखित ग्राफिक रूप से प्राप्त किया जाता है:

अधिक डेरिवेटिव कैलकुलेटर

इसके अलावा रत्न , आप बहुत कुछ पा सकते हैं जो डेरिवेटिव के आधार पर अलग -अलग चीजें करते हैं।भेदभाव, अनुप्रयोगों के एक व्यापक स्पेक्ट्रम के साथ कैलकुलस, भौतिकी, इंजीनियरिंग और अर्थशास्त्र में एक महत्वपूर्ण ऑपरेशन है।

अधिक चर के लिए एक रैखिक सन्निकटन का संचालन करने का एक तरीका भी है, यह उदाहरण के लिए है, एक फ़ंक्शन \ f (x, y) \) के लिए, जिस स्थिति में रैखिक सन्निकटन सूत्र \(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\)हो जाता है, इसलिए इस मामले में, फिर इस मामले में,रैखिककरण को खोजने के लिए हमें उपयोग करने की आवश्यकता है आंशिक अवकलज ।

Finding the linearization of a function is not by far the only thing you can do with derivatives. Differentiation is a relatively easy operation with simple rules like the पmurauguth नियम , तंग और यह तिहाई यह डेरिवेटिव की गणना को अपेक्षाकृत सीधा ऑपरेशन बनाता है।

हालांकि यह सरल माना जाता है, यह एक अच्छा विचार है वthaumaumaut r कैलकुलेटry दिखाए गए सभी चरणों को प्राप्त करने के लिए, सभी के स्पष्ट उल्लेख के साथ वmuntumam नियम इस्तेमाल किया गया।