समाधानकर्ताओं गणना

व्युत्पन्न नियम

सराय: इस व्युत्पन्न कैलकुलेटर का उपयोग करें, जो आपके द्वारा प्रदान किए गए किसी भी फ़ंक्शन के व्युत्पन्न को खोजने के लिए, सबसे आम व्युत्पन्न नियमों का उपयोग करते हुए, सभी चरणों को दिखाते हुए।कृपया उस फ़ंक्शन को टाइप करें जिसे आप नीचे दिए गए फॉर्म बॉक्स में व्युत्पन्न नियम लागू करना चाहते हैं।

व्युत्पन्न नियमों के बारे में

यह कैलकुलेटर आपको आवश्यक बुनियादी विभेदन नियमों को लागू करके, प्रक्रिया के सभी चरणों को दिखाते हुए, और प्रत्येक नियम को लागू करने पर ध्यान देने के लिए आपके द्वारा प्रदान किए गए फ़ंक्शन के व्युत्पन्न की गणना करने की अनुमति देगा।

आपको बस एक वैध फ़ंक्शन प्रदान करने की आवश्यकता है जो अलग है (जिसका अर्थ है कि इसमें एक व्युत्पन्न है)।उदाहरण के लिए, एक मान्य फ़ंक्शन f (x) = 1/3*x*sin (x) हो सकता है, बस एक उदाहरण का उल्लेख करने के लिए।

फिर, जब आप पहले से ही अपना फ़ंक्शन टाइप कर चुके हैं, तो आप दिखाए गए भेदभाव के सभी चरणों को प्राप्त करने के लिए "गणना" पर क्लिक करते हैं।

डेरिवेटिव के नियमों की सादगी भेदभाव की प्रक्रिया को एक 'आसान' के रूप में मान्यता प्राप्त है, एक निर्णय जो शायद एक ओवरस्टेटमेंट है।

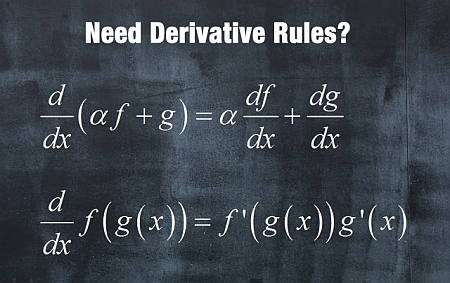
मूल व्युत्पन्न नियम

आपको सीखने के लिए चार बुनियादी व्युत्पन्न नियम हैं

रत्न:: कार्यों के लिए \(f(x)\) और \(g(x)\), और एक निरंतर \(a\), फिर व्युत्पन्न एक रैखिक ऑपरेशन है: \((af(x)+g(x))' = af'(x)+g'(x)\)
पmurauguth नियम कार्यों के लिए \(f(x)\) और \(g(x)\), उत्पाद का व्युत्पन्न \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\) है
Vayan नियम: कार्यों के लिए \(f(x)\) और \(g(x)\), भागफल का व्युत्पन्न है \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
तिहाई कार्यों के लिए \(f(x)\) और \(g(x)\), समग्र फ़ंक्शन का व्युत्पन्न \((f(g(x)))' = f'(g(x))g'(x)\) है

यह नियम एक आकर्षण की तरह काम करेंगे और आपको किसी भी बुनियादी फ़ंक्शन के व्युत्पन्न को खोजने में मदद करेंगे।

व्युत्पन्न नियमों का उपयोग कैसे करें?

Letsunt 1: फ़ंक्शन f (x) की पहचान करें जिसे आप अलग करना चाहते हैं, यदि आवश्यक हो तो सरल करें
Therur the: रैखिकता का उपयोग करते हुए, फ़ंक्शन को छोटे व्युत्पन्न चंक्स में तोड़ने का प्रयास करें
Theirण 3: फ़ंक्शन f (x) की संरचना के आधार पर, किसी भी उपलब्ध नियमों (उत्पाद, भागफल और श्रृंखला नियम) का उपयोग करें, और ध्यान रखें कि आपको कई नियमों को लगातार लागू करने की आवश्यकता हो सकती है)

आमतौर पर आप कई भेदभाव नियमों के संयोजन को समाप्त कर देंगे, जब तक कि आप बिंदु तक नहीं पहुंचेंगे, जहां आप एक प्राथमिक कार्य नहीं पा लेते हैं, जिनमें से आप पहले से ही जानते हैं कि कैसे अंतर करना है।

क्या मैं सभी डेरिवेटिव को हल कर सकता हूं

यह कहते हुए कि भेदभाव नियमों का उपयोग करने से आप सभी डेरिवेटिव को हल कर सकते हैं, एक ओवरस्टेटमेंट हो सकता है।आप अधिकांश डेरिवेटिव, और निश्चित रूप से सभी बुनियादी लोगों को हल करने में सक्षम होंगे, लेकिन ऐसे कार्य हैं जिनके पास कम सहज व्यवहार है जिसे परिभाषित किया जा सकता है, हालांकि वे आमतौर पर बुनियादी कैलकुलस पाठ्यक्रमों में नहीं हैं।

बुनियादी कार्यों के संबंध में, उनमें से अधिकांश को एक समस्या के बिना विभेदित किया जाएगा।

ए तमाम , तंग या अफ़्री अलगाव में होने की संभावना नहीं है, और संभवतः कई नियमों के अनुक्रम में आएंगे जिन्हें एक साथ उपयोग करने की आवश्यकता है।

उदाहरण: व्युत्पन्न नियम

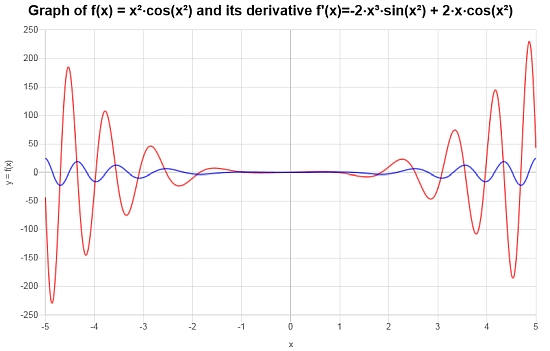
बुनियादी व्युत्पन्न नियमों का उपयोग करते हुए, निम्नलिखित व्युत्पन्न की गणना करें: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)

तमाम: आइए हम निम्नलिखित दिए गए फ़ंक्शन पर विचार करें, जिसके लिए व्युत्पन्न की गणना करने की आवश्यकता है \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)

फ़ंक्शन को सरलीकरण की आवश्यकता नहीं है, इसलिए हम सीधे इसके व्युत्पन्न की गणना में जा सकते हैं:

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

फ़ंक्शन का संबंधित ग्राफ और इसके व्युत्पन्न को नीचे दिखाया गया है:

उदाहरण: अधिक व्युत्पन्न नियम

निम्नलिखित व्युत्पन्न की गणना करें: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) बुनियादी व्युत्पन्न नियमों का उपयोग करके।

तमाम: अब, हाथ में कार्य फ़ंक्शन को अलग करना है \(\displaystyle f(x)=x\cos\left(x^2+1\right)\)

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

व्युत्पन्न नियमों का उदाहरण

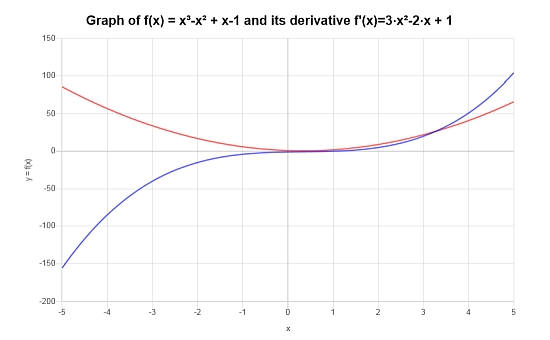
फ़ंक्शन के लिए \( f(x) = (x-1)(x^2+1) \), इसके व्युत्पन्न को खोजने के लिए व्युत्पन्न नियमों का उपयोग करें।

तमाम: इस अंतिम उदाहरण के लिए, हमें अंतर करने की आवश्यकता है: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)।

पraurauraurauray: इस मामले में, हमें पहले दिए गए फ़ंक्शन का विस्तार करने की आवश्यकता है \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \), और ऐसा करने के लिए, हम निम्नलिखित सरलीकरण चरणों का संचालन करते हैं:

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

फ़ंक्शन का विस्तार करने के बाद, हम व्युत्पन्न की गणना के लिए आगे बढ़ सकते हैं:

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2-2x+1\)

ग्राफिक रूप से, यह कैसे कार्य और इसके व्युत्पन्न रूप है:

अधिक व्युत्पन्न कैलकुलेटर

One of the magic about differentiation is that you can तमाम कुछ बुनियादी और सरल नियमों का उपयोग करते हुए किसी भी फ़ंक्शन, सहित पmurauguth नियम , तंग और स्वाभाविक रूप से, रोटी ।यह छोटा शस्त्रागार आमतौर पर आपके लिए आवश्यक किसी भी व्युत्पन्न की गणना करने के लिए पर्याप्त है

भेदभाव और एकीकरण कैलकुलस में मुख्य लेन हैं, बिना किसी विवाद के, क्योंकि वे विज्ञान के सभी पहलुओं में इतने सारे अनुप्रयोगों के केंद्र हैं।संबंधित दरों से अँगुला , साथ आंशिक अवकलज भौतिकी और अर्थशास्त्र में