समाधानकर्ताओं गणना

भागफल नियम

सराय: इस भागफल नियम कैलकुलेटर का उपयोग करें जो कि आपके द्वारा प्रदान किए गए उद्धरणों से जुड़े फ़ंक्शन के व्युत्पन्न को खोजने के लिए, सभी चरणों को दिखाते हैं।कृपया नीचे दिए गए फ़ॉर्म बॉक्स में फ़ंक्शन टाइप करें।

भागफल नियम

यह कैलकुलेटर आपको एक फ़ंक्शन के लिए भागफल नियम का उपयोग करने की अनुमति देगा जिसमें एक भागफल शामिल है, जो प्रक्रिया के सभी चरणों को दर्शाता है।आपको केवल एक मान्य विभाज्य कार्य प्रदान करने की आवश्यकता है।इस फ़ंक्शन को लागू होने के लिए भागफल नियम के लिए कम से कम एक भागफल को शामिल करने की आवश्यकता है।

एक मान्य फ़ंक्शन का एक उदाहरण f (x) = (x^2 + 2x + 1)/(x^2-1), या f (x) = sin (x)/x, आदि।

एक बार एक मान्य फ़ंक्शन जो उद्धरण प्रदान किया जाता है, आपको दिखाए गए गणना के चरणों को प्राप्त करने के लिए "गणना" बटन पर क्लिक करना होगा।

के साथ पmurauguth नियम और तिहाई , तंग सबसे महत्वपूर्ण बुनियादी में से एक है वmuntumam नियम ।

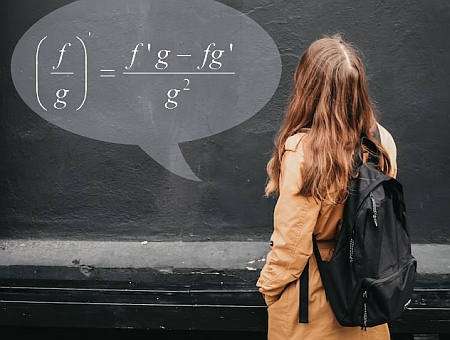
भागफल नियम सूत्र

सरल शब्दों में, तंग व्यक्तिगत कार्यों और उनके डेरिवेटिव के ज्ञान का उपयोग करते हुए, एक भागफल के व्युत्पन्न की गणना करने में आपकी मदद करता है।भागफल नियम सूत्र है:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

भागफल नियम का उपयोग करने के लिए क्या कदम हैं?

Letsunt 1: स्पष्ट रूप से फ़ंक्शंस f (x) और g (x) को पहचानें जो कि भागीदार के अंश और भाजक में जाते हैं
Therur the: किसी भी स्पष्ट शब्द को सरल बनाएं जिसे सरल बनाया जा सकता है
Theirण 3: संबंधित डेरिवेटिव f '(x) और g' (x) की गणना करें
Reyrur 4: फॉर्मूला में चरण 3 में पाए गए मानों को प्लग करें \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

ध्यान दें कि f (x) और g (x) अभी भी जटिल कार्य हो सकते हैं, इसलिए आपको f '(x) और g' (x) दोनों की गणना करने के लिए चेन नियम जैसे अन्य नियमों का उपयोग करने की आवश्यकता हो सकती है।

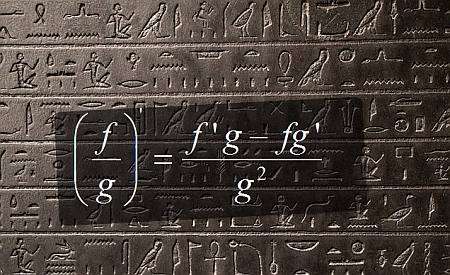
भागफल नियम व्युत्पन्न

एक भागफल नियम व्युत्पन्न की गणना करते समय, आप व्यक्तिगत डेरिवेटिव के ज्ञान के लिए एक भागफल के व्युत्पन्न को कम कर रहे हैं, लेकिन उन व्यक्तिगत डेरिवेटिव को अभी भी कई चरणों की आवश्यकता हो सकती है व elcuntumaut नियम नियम हल करने के लिए।

यही कारण है कि भेदभाव को एक 'सीधा' ऑपरेशन माना जाता है, लेकिन फिर भी, आपको पर्याप्त रूप से संगठित करने की आवश्यकता है और व्युत्पन्न नियमों के साथ विघटित होने पर उत्पन्न होने वाले सभी टुकड़ों पर नज़र रखने की आवश्यकता है, और फिर छोटे टुकड़ों के साथ आगे बढ़ें जो अधिक भेदभाव नियमों की आवश्यकता हो सकती हैलागू।

तो आप एक पुनरावृत्ति प्रक्रिया के साथ समाप्त हो सकते हैं, लेकिन यह प्रत्येक छोटे हिस्से में गहराई तक जाने से कुछ बिंदु पर समाप्त होने की गारंटी है, जब तक कि आप एक प्राथमिक व्युत्पन्न नहीं पाते हैं, बहुपद या एक क्योरहमकम ।

विभेदीकरण में भागफल नियम

की भूमिका Rayrण में kana नियम नियम बहुत महत्वपूर्ण है, एक अच्छा कारण है कि आप इसके लिए एक कैलकुलेटर का उपयोग क्यों करना चाहेंगे।बीजगणितीय शब्दों में, भागफल नियम को उत्पाद नियम की तुलना में अधिक जटिल माना जा सकता है, और यह कई मामलों में सच हो सकता है, लेकिन फिर भी यह अंततः अंश और हर में कार्यों की जटिलता पर निर्भर करता है।

भागफल नियम उदाहरण

फ़ंक्शन पर विचार करें: \(f(x) = \frac{x^2+1}{x-2}\), इसका व्युत्पन्न खोजें।

तमाम: इस उदाहरण के लिए, हमें इसके व्युत्पन्न को खोजने के संदर्भ में फ़ंक्शन \(\displaystyle f(x)=\frac{x^2+1}{x-2}\) का विश्लेषण करने की आवश्यकता है।

\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)

By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Removing unnecessary parentheses and multiplying the terms by \(-1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)

Aggregating those terms with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)

Putting together the numerical values and operating the terms that were grouped with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)

तिहाई : हम पाते हैं कि दिए गए फ़ंक्शन का व्युत्पन्न है:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

तो फिर, फ़ंक्शन का चित्रमय चित्रण और इसके व्युत्पन्न है \([-5, 5]\):

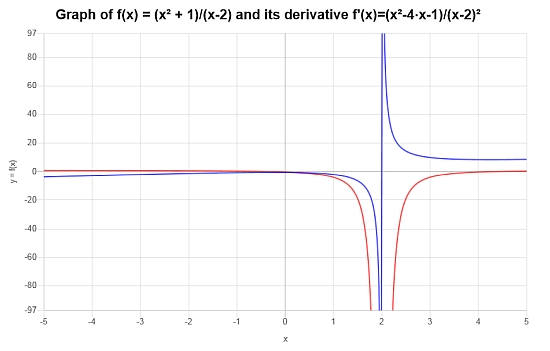
उदाहरण: भागफल नियम गणना

अब विचार करें \(f(x) = \frac{x}{\sin(x)}\), भागफल नियम का उपयोग करके इसके व्युत्पन्न को खोजें।

तमाम: इस दूसरे उदाहरण के लिए, जिस फ़ंक्शन में हम रुचि रखते हैं, वह \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\) है।आइए इसे भागफल नियम का उपयोग करके अलग करें।

\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

तिहाई : निष्कर्ष यह है कि, उपरोक्त गणना के आधार पर, व्युत्पन्न द्वारा दिया जाता है:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

ग्राफिक रूप से, हम फ़ंक्शन (नीले रंग में) और इसके व्युत्पन्न (लाल रंग में) देख सकते हैं:

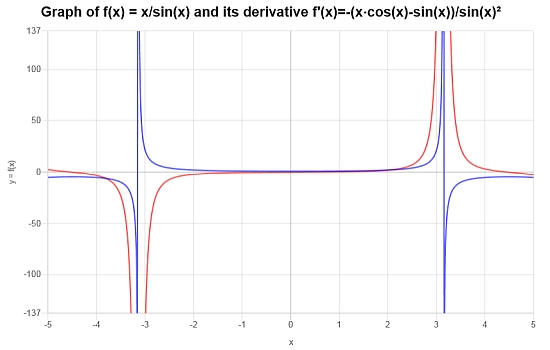
अधिक भागफल नियम उदाहरण

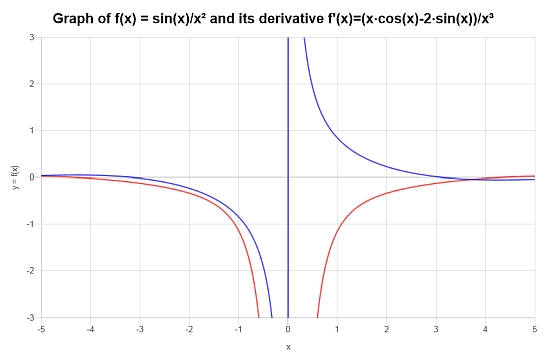
अंत में, फ़ंक्शन पर विचार करें: \(f(x) = \frac{\sin(x)}{x^2}\), इसके व्युत्पन्न को खोजें।

तमाम: इस अंतिम भागफल नियम उदाहरण के लिए हम फ़ंक्शन \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\) के साथ काम करते हैं।।

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)

The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)

By simplifying and regrouping terms

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)

तिहाई : दिए गए फ़ंक्शन के लिए, इसका व्युत्पन्न है:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

नीचे दिए गए ग्राफ में \(f\) और \(f'\) के लिए स्थिति को दर्शाया गया है:

अधिक व्युत्पन्न कैलकुलेटर

कैलकुलस में आप करेंगे डे डे खोजें हर जगह आप देखते हैं।हजारों अनुप्रयोग हैं जो उन्हें विज्ञान और इंजीनियरिंग के लिए सबसे महत्वपूर्ण उपकरणों पर बनाते हैं।

आपको इसके बारे में जानने की आवश्यकता होगी अँगुला अलग -अलग अनुप्रयोगों के लिए अक्सर संबंधित दरों को शामिल करते हुए, या बहुभिन्नरूपी पथरी में आप रुचि रखते हैं अफ़रोट ।

यदि आप सबसे आम को ठीक से संभालने में सक्षम हैं, तो कुल मिलाकर, आप अपने जीवन को आसान पाएंगे वmuntumam नियम , ये शामिल हैं तिहाई के रूप में भी पmurauguth नियम और तंग ।